Wikimedia-ID.github.io
Soal Project Euler dalam Bahasa Indonesia
Berikut adalah soal2 Project Euler dalam bahasa Indonesia
Daftar IsiSoal 1
Jika kita membuat daftar semua bilangan asli yang lebih kecil daripada 10 yang merupakan kelipatan 3 atau 5, maka kita akan mendapatkan 3, 5, 6, dan 9. Jumlah dari bilangan-bilangan tersebut adalah 23.
Tentukanlah jumlah dari semua bilangan kelipatan 3 atau 5 yang lebih kecil daripada 1000.
Answer: e1edf9d1967ca96767dcc2b2d6df69f4
Soal 2
Setiap pola baru dalam barisan Fibonacci dibentuk dengan menjumlahkan dua buah bilangan sebelumnya. Jika kita memulai barisan dengan angka 1 dan 2, maka 10 bilangan pertama barisan Fibonacci adalah:
Tentukanlah hasil penjumlahan semua bilangan genap yang lebih kecil dari empat juta dalam barisan Fibonacci seperti di atas.
Answer: 4194eb91842c8e7e6df099ca73c38f28
Soal 3
Faktor prima dari 13195 adalah 5, 7, 13, dan 29.
Berapakah faktor prima terbesar dari bilangan 600851475143 ?
Answer: 94c4dd41f9dddce696557d3717d98d82
Soal 4
Sebuah bilangan disebut sebagai palindrom, bila kita membacanya baik dari depan maupun dari belakang, kita akan mendapatkan bilangan yang sama. Bilangan palindrom terbesar hasil dari perkalian dua buah bilangan 2 digit adalah 9009 = 91 × 99.
Tentukan bilangan palindrom terbesar hasil dari perkalian dua buah bilangan 3 digit.
Answer: d4cfc27d16ea72a96b83d9bdef6ce2ec
Soal 5
2520 adalah bilangan terkecil yang dapat habis dibagi oleh semua angka dari 1 sampai 10.
Berapakah bilangan positif terkecil yang dapat habis dibagi oleh semua bilangan dari 1 sampai 20?
Answer: bc0d0a22a7a46212135ed0ba77d22f3a
Soal 6
Jumlah dari kuadrat sepuluh bilangan asli pertama adalah,
Kuadrat dari jumlah sepuluh bilangan asli pertama adalah,
Selisih antara jumlah dari kuadrat dengan kuadrat dari jumlah sepuluh bilangan asli pertama adalah 3025 - 385 = 2640. Tentukan selisih antara jumlah dari kuadrat dengan kuadrat dari jumlah seratus bilangan asli pertama.
Answer: 867380888952c39a131fe1d832246ecc
Soal 7
Bila kita membuat daftar enam bilangan prima pertama: 2, 3, 5, 7, 11, dan 13, kita dapat melihat bahwa bilangan prima ke-6 adalah 13.
Berapakah bilangan prima ke-10 001?
Answer: 8c32ab09ec0210af60d392e9b2009560
Soal 8
Empat bilangan berurutan dari 1000 bilangan berikut yang memiliki hasil kali terbesar adalah 9 × 9 × 8 × 9 = 5832.
Temukanlah tiga belas bilangan berurutan dari 1000 bilangan di atas yang memiliki hasil kali terbesar. Berapakah hasil kali ketiga belas bilangan tersebut?
Answer: 0f53ea7949d32ef24f9186207600403c
Soal 9
Triplet Pythagoras adalah kumpulan tiga buah bilangan asli, a < b < c, yang memenuhi,
Sebagai contoh, 32 + 42 = 9 + 16 = 25 = 52.
Dan hanya terdapat persis satu triplet Pythagoras yang bisa memenuhi a + b + c = 1000. Temukan triplet Pythagoras tersebut dan tentukanlah hasil a × b × c.
Answer: 24eaa9820350012ff678de47cb85b639
Soal 10
Jumlah semua bilangan prima yang lebih kecil daripada 10 adalah 2 + 3 + 5 + 7 = 17.
Tentukanlah jumlah semua bilangan prima yang lebih kecil dari dua juta (2 000 000).
Answer: d915b2a9ac8749a6b837404815f1ae25
Soal 11
Pada kisi berukuran 20×20 berikut, empat buah bilangan yang membentuk satu garis diagonal lurus telah ditandai dengan warna merah.
08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08
49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00
81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65
52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91
22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80
24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50
32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70
67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21
24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72
21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95
78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92
16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57
86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58
19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40
04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66
88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69
04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36
20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16
20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54
01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48
Hasil perkalian dari bilangan tersebut adalah 26 × 63 × 78 × 14 = 1788696.
Berapakah hasil perkalian terbesar dari empat bilangan berurutan dalam satu garis lurus (atas, bawah, kiri, kanan, atau diagonal) pada kisi berukuran 20×20 di atas?
Answer: 678f5d2e1eaa42f04fa53411b4f441ac
Soal 12
Barisan bilangan segitiga dibuat dengan menjumlahkan bilangan asli. Maka bilangan segitiga ke-7 adalah 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. Sepuluh bilangan segitiga pertama adalah:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
Jika kita membuat daftar faktor dari tujuh bilangan segitiga pertama:
1: 1
3: 1,3
6: 1,2,3,6
10: 1,2,5,10
15: 1,3,5,15
21: 1,3,7,21
28: 1,2,4,7,14,28
Dapat terlihat bahwa 28 adalah bilangan segitiga pertama yang memiliki lebih dari lima faktor. Berapakah bilangan segitiga pertama yang memiliki lebih dari lima ratus faktor?
Answer: 8091de7d285989bbfa9a2f9f3bdcc7c0
Soal 13
Carilah sepuluh angka pertama dari hasil penjumlahan seratus buah bilangan 50 digit berikut ini.
46376937677490009712648124896970078050417018260538
74324986199524741059474233309513058123726617309629
91942213363574161572522430563301811072406154908250
23067588207539346171171980310421047513778063246676
89261670696623633820136378418383684178734361726757
28112879812849979408065481931592621691275889832738
44274228917432520321923589422876796487670272189318
47451445736001306439091167216856844588711603153276
70386486105843025439939619828917593665686757934951
62176457141856560629502157223196586755079324193331
64906352462741904929101432445813822663347944758178
92575867718337217661963751590579239728245598838407
58203565325359399008402633568948830189458628227828
80181199384826282014278194139940567587151170094390
35398664372827112653829987240784473053190104293586
86515506006295864861532075273371959191420517255829
71693888707715466499115593487603532921714970056938
54370070576826684624621495650076471787294438377604
53282654108756828443191190634694037855217779295145
36123272525000296071075082563815656710885258350721
45876576172410976447339110607218265236877223636045
17423706905851860660448207621209813287860733969412
81142660418086830619328460811191061556940512689692
51934325451728388641918047049293215058642563049483
62467221648435076201727918039944693004732956340691
15732444386908125794514089057706229429197107928209
55037687525678773091862540744969844508330393682126
18336384825330154686196124348767681297534375946515
80386287592878490201521685554828717201219257766954
78182833757993103614740356856449095527097864797581
16726320100436897842553539920931837441497806860984
48403098129077791799088218795327364475675590848030
87086987551392711854517078544161852424320693150332
59959406895756536782107074926966537676326235447210
69793950679652694742597709739166693763042633987085
41052684708299085211399427365734116182760315001271
65378607361501080857009149939512557028198746004375
35829035317434717326932123578154982629742552737307
94953759765105305946966067683156574377167401875275
88902802571733229619176668713819931811048770190271
25267680276078003013678680992525463401061632866526
36270218540497705585629946580636237993140746255962
24074486908231174977792365466257246923322810917141
91430288197103288597806669760892938638285025333403
34413065578016127815921815005561868836468420090470
23053081172816430487623791969842487255036638784583
11487696932154902810424020138335124462181441773470
63783299490636259666498587618221225225512486764533
67720186971698544312419572409913959008952310058822
95548255300263520781532296796249481641953868218774
76085327132285723110424803456124867697064507995236
37774242535411291684276865538926205024910326572967
23701913275725675285653248258265463092207058596522
29798860272258331913126375147341994889534765745501
18495701454879288984856827726077713721403798879715
38298203783031473527721580348144513491373226651381
34829543829199918180278916522431027392251122869539
40957953066405232632538044100059654939159879593635
29746152185502371307642255121183693803580388584903
41698116222072977186158236678424689157993532961922
62467957194401269043877107275048102390895523597457
23189706772547915061505504953922979530901129967519
86188088225875314529584099251203829009407770775672
11306739708304724483816533873502340845647058077308
82959174767140363198008187129011875491310547126581
97623331044818386269515456334926366572897563400500
42846280183517070527831839425882145521227251250327
55121603546981200581762165212827652751691296897789
32238195734329339946437501907836945765883352399886
75506164965184775180738168837861091527357929701337
62177842752192623401942399639168044983993173312731
32924185707147349566916674687634660915035914677504
99518671430235219628894890102423325116913619626622
73267460800591547471830798392868535206946944540724
76841822524674417161514036427982273348055556214818
97142617910342598647204516893989422179826088076852
87783646182799346313767754307809363333018982642090
10848802521674670883215120185883543223812876952786
71329612474782464538636993009049310363619763878039
62184073572399794223406235393808339651327408011116
66627891981488087797941876876144230030984490851411
60661826293682836764744779239180335110989069790714
85786944089552990653640447425576083659976645795096
66024396409905389607120198219976047599490197230297
64913982680032973156037120041377903785566085089252
16730939319872750275468906903707539413042652315011
94809377245048795150954100921645863754710598436791
78639167021187492431995700641917969777599028300699
15368713711936614952811305876380278410754449733078
40789923115535562561142322423255033685442488917353
44889911501440648020369068063960672322193204149535
41503128880339536053299340368006977710650566631954
81234880673210146739058568557934581403627822703280
82616570773948327592232845941706525094512325230608
22918802058777319719839450180888072429661980811197
77158542502016545090413245809786882778948721859617
72107838435069186155435662884062257473692284509516
20849603980134001723930671666823555245252804609722
53503534226472524250874054075591789781264330331690
Answer: 361113f19fd302adc31268f8283a4f2d
Soal 14
Sebuah barisan iteratif berikut didefinisikan untuk himpunan bilangan bulat positif dengan aturan:
n → n/2 (n ∈ bilangan genap)
n → 3n + 1 (n ∈ bilangan ganjil)
Menggunakan aturan di atas, dimulai dari 13, maka kita akan mendapatkan barisan:</br>
Dapat terlihat bahwa barisan ini (yang dimulai dari 13 dan berakhir di 1) memiliki 10 suku. Meskipun belum ada bukti matematisnya, diperkirakan bahwa apapun bilangan awalnya, barisan seperti ini akan selalu berakhir di 1 (Masalah Collatz).</br> Bilangan awal manakah yang besarnya lebih kecil daripada satu juta yang akan menghasilkan barisan terpanjang?</br>
Catatan : besar suku berikutnya (setelah bilangan awal) dalam barisan boleh melebihi satu juta.
Answer: 5052c3765262bb2c6be537abd60b305e
Soal 15
Jika kita mulai bergerak dari pojok kiri atas kisi berukuran 2×2, dan hanya boleh bergerak ke kanan atau ke bawah, maka akan ada persis 6 ruas rute menuju ke pojok kanan bawah.
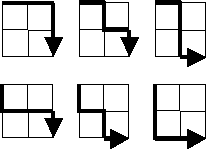
Berapakah jumlah rute yang ada jika kisi berukuran 20×20?
Answer: 928f3957168ac592c4215dcd04e0b678
Soal 16
215 = 32768 dan jumlah semua digitnya adalah 3 + 2 + 7 + 6 + 8 = 26.
Berapakah jumlah digit dari angka 21000?
Answer: 6a5889bb0190d0211a991f47bb19a777
Soal 17
Angka 1 sampai 5 ditulis dalam kata bahasa Inggris sebagai : one, two, three, four, five, dan terdapat 3 + 3 + 5 + 4 + 4 = 19 jumlah huruf yang digunakan.
Bila semua angka dari 1 sampai 1000 (1 dan 1000 termasuk di dalamnya) ditulis dalam kata bahasa Inggris, berapakah jumlah huruf yang digunakan?
Catatan : Karena hanya terdapat 16384 jalur, maka masalah ini mungkin diselesaikan dengan mencoba semua jalur satu persatu. Tetapi, pada soal no.67, terdapat tantangan yang sama namun dengan menggunakan segitiga 100 baris. Masalah itu tidak bisa diselesaikan dengan mencoba jalur satu persatu dan dibutuhkan cara yang cerdik! ;o)
Answer: 6a979d4a9cf85135408529edc8a133d0
Soal 18
Dengan memulai dari puncak segitiga seperti gambar berikut, dan berpindah ke angka sebelah kiri atau kanan pada baris di bawahnya, maka akan didapat jumlah bilangan maksimum dari atas sampai bawah adalah 23.
3
7 4
2 4 6
8 5 9 3
Jumlahnya, 3 + 7 + 4 + 9 = 23.
Berapakah jumlah bilangan maksimum dengan cara serupa dari atas ke bawah pada segitiga berikut:
75
95 64
17 47 82
18 35 87 10
20 04 82 47 65
19 01 23 75 03 34
88 02 77 73 07 63 67
99 65 04 28 06 16 70 92
41 41 26 56 83 40 80 70 33
41 48 72 33 47 32 37 16 94 29
53 71 44 65 25 43 91 52 97 51 14
70 11 33 28 77 73 17 78 39 68 17 57
91 71 52 38 17 14 91 43 58 50 27 29 48
63 66 04 68 89 53 67 30 73 16 69 87 40 31
04 62 98 27 23 09 70 98 73 93 38 53 60 04 23
Catatan : Karena hanya terdapat 16384 jalur, maka masalah ini mungkin diselesaikan dengan mencoba semua jalur satu persatu. Tetapi, pada soal no.67, terdapat tantangan yang sama namun dengan menggunakan segitiga 100 baris, sehingga tidak bisa diselesaikan dengan mencoba jalur satu persatu dan membutuhkan cara yang cerdas! ;o)
Answer: 708f3cf8100d5e71834b1db77dfa15d6
Soal 19
Anda diberikan informasi sebagai berikut, dan Anda diminta untuk melakukan penelitian.
- 1 Jan 1900 adalah hari Senin.
- Bulan yang panjangnya tiga puluh hari adalah September, April, Juni, dan November. Sisanya memiliki panjang tiga puluh satu hari, kecuali Februari yang panjangnya dua puluh delapan hari, dan pada tahun kabisat bisa menjadi dua puluh sembilan.
- Tahun kabisat adalah tahun yang dapat habis dibagi 4, namun tidak berlaku pada tahun akhir abad, kecuali tahun tersebut tersebut habis dibagi 400. (Contoh : Februari 1900, akhir abad ke-19, memiliki dua puluh delapan hari walaupun 1900 habis dibagi 4)
Berapakah banyak hari Minggu yang jatuh pada tanggal 1 pada abad ke-20 (1 Jan 1901 sampai 31 Des 2000)?
Answer: a4a042cf4fd6bfb47701cbc8a1653ada
Soal 20
n! (dibaca n faktorial) didefinisikan sebagai n × (n − 1) × … × 3 × 2 × 1.
Sebagai contoh, 10! = 10 × 9 × … × 3 × 2 × 1 = 3628800.
Jumlah digit bilangan 10! adalah 3 + 6 + 2 + 8 + 8 + 0 + 0 = 27.
Carilah jumlah digit dari bilangan 100!
Answer: 443cb001c138b2561a0d90720d6ce111
Soal 21
Misalkan d(n) adalah jumlah semua bilangan yang lebih kecil daripada n yang dapat membagi habis n.
Jika d(a)=b dan d(b)=a, dengan a≠b, maka a dan b adalah sebuah pasangan akrab, dan a serta b dapat disebut bilangan akrab.
Sebagai contoh, bilangan-bilangan yang dapat membagi habis 220 dan lebih kecil daripada 220 adalah 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, dan 110; maka d(220)=284. Bilangan yang dapat membagi habis 284 dan lebih kecil daripada 2784 adalah 1, 2, 4, 71, dan 142; maka d(284)=220.
Hitunglah jumlah semua bilangan akrab yang lebih kecil daripada 10000.
Answer: 51e04cd4e55e7e415bf24de9e1b0f3ff
Soal 22
[names.txt](/projecteuler/files/names.txt) (klik kanan dan pilih 'Save Link/Target As...') , adalah 46K berkas teks yang berisi lebih dari lima ribu nama depan. Urutkanlah nama-nama tersebut berdasarkan abjad, lalu hitunglah nilai dari setiap nama dengan cara mengkonversikan setiap huruf menjadi angka sesuai dengan urutan alfabet. Setelah itu kalikan jumlah angka-angka tersebut dengan posisinya pada daftar nama names.txt yang telah diurutkan.
Sebagai contoh, saat daftar nama sudah diurutkan berdasarkan abjad, COLIN berada di posisi ke 938 pada daftar nama, dari huruf-hurufnya COLIN akan memiliki nilai 3 + 15 + 12 + 9 + 14 = 53. Sehingga, COLIN akan memiliki nilai 938 × 53 = 49714.
Berapakah jumlah nilai dari semua nama pada names.txt?
Answer: f2c9c91cb025746f781fa4db8be3983f
Soal 23
Bilangan sempurna adalah sebuah bilangan yang jumlah semua pembagi habisnya sama dengan bilangan itu sendiri. Sebagai contoh, jumlah pembagi habis dari 28 adalah 1 + 2 + 4 + 7 + 14 = 28, dengan demikian 28 adalah bilangan sempurna.
Sebuah bilangan n disebut defisien jika jumlah pembagi habisnya kurang dari n, dan disebut limpahan jika jumlahnya melebihi n.
12 adalah bilangan limpahan terkecil, 1 + 2 + 3 + 4 + 6 = 16, sedangkan bilangan terkecil yang dapat dibentuk dari hasil jumlah dua buah bilangan limpahan adalah 24. Dengan analisis matematis, dapat dibuktikan bahwa semua bilangan bulat lebih dari 28123 dapat dibentuk dari penjumlahan dua buah bilangan limpahan. Dan, batas ini tidak bisa diperkecil lagi oleh analisis lebih lanjut, sehingga bilangan terbesar yang tidak dapat dibentuk dari penjumlahan dua buah bilangan limpahan adalah kurang dari batas ini (28123).
Carilah jumlah semua bilangan positif yang tidak bisa dibentuk dari penjumlahan dua buah bilangan limpahan.
Answer: 2c8258c0604152962f7787571511cf28
Soal 24
Permutasi adalah susunan terurut dari objek. Sebagai contoh, 3124 adalah salah satu permutasi yang mungkin dari digit 1, 2, 3, dan 4. Jika semua permutasi dituliskan sesuai dengan urutan angka atau alfabet, maka kita sebut itu sebagai susunan leksikografis. Susunan leksikografis dari permutasi 0, 1, dan 2 adalah:
Berapakah suku kesatu juta dari susunan leksikografis dari permutasi digit 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9?
Answer: 7f155b45cb3f0a6e518d59ec348bff84
Soal 25
Barisan Fibonacci dibentuk dari hubungan berulang:
Fn = Fn−1 + Fn−2, di mana F1 = 1 and F2 = 1.
Dari aturan tersebut didapatkan 12 suku pertamanya:
F1 = 1
F2 = 1
F3 = 2
F4 = 3
F5 = 5
F6 = 8
F7 = 13
F8 = 21
F9 = 34
F10 = 55
F11 = 89
F12 = 144
Suku ke-12, yaitu F12, adalah suku pertama yang memiliki tiga digit.
Suku keberapakah pada barisan Fibonacci yang pertama kali memiliki 1000 digit?
Answer: a376802c0811f1b9088828288eb0d3f0
Soal 26
Unit pecahan adalah sebuah pecahan yang memiliki pembilang 1. Representasi desimal dari unit pecahan untuk penyebut dari 2 sampai 10 adalah sebagai berikut:
1/2 = 0.5 1/3 = 0.(3) 1/4 = 0.25 1/5 = 0.2 1/6 = 0.1(6) 1/7 = 0.(142857) 1/8 = 0.125 1/9 = 0.(1) 1/10 = 0.1
Di sini 0.1(6) berarti 0.166666..., dan memiliki 1 digit yang berulang. Dapat kita lihat bahwa 1/7 memiliki 6 digit yang berulang.
Carilah berapa nilai dari d < 1000, bila 1/d memiliki paling banyak digit berulang dalam bentuk desimalnya.
Answer: 6aab1270668d8cac7cef2566a1c5f569
Soal 27
Euler menemukan sebuah rumus kuadrat yang luar biasa:
n² + n + 41
Ternyata rumus tersebut akan menciptakan 40 buah bilangan prima untuk nilai n = 0 sampai 39. Tetapi, saat n = 40, 402 + 40 + 41 = 40(40 + 1) + 41 angka ini ternyata habis dibagi 41, dan saat n = 41, 41² + 41 + 41 angka ini juga habis dibagi 41.
Rumus luar biasa lainnya n² − 79n + 1601 telah ditemukan, rumus tersebut akan menghasilkan 80 buah bilangan prima untuk nilai n = 0 to 79. Hasil kali dari koefisien rumus tersebut, −79 dan 1601, adalah −126479.
Dengan bentuk kuadrat berikut ini:
n² + an + b, di mana |a| < 1000 dan |b| < 1000
di mana |n| adalah nilai mutlak/absolut dari n
sebagai contoh: |11| = 11 dan |−4| = 4
Carilah hasil kali koefisien, a dan b, untuk rumus kuadrat di atas yang menghasilkan paling banyak bilangan prima untuk nilai n berurutan, dimulai dari n = 0.
Answer: 69d9e3218fd7abb6ff453ea96505183d
Soal 28
Dimulai dari angka 1 di tengah, lalu bergerak ke kanan searah jarum jam, maka dapat dibentuk spiral angka berukuran 5 x 5 sebagai berikut:
21 22 23 24 25
20 7 8 9 10
19 6 1 2 11
18 5 4 3 12
17 16 15 14 13
Dapat terlihat bahwa jumlah angka-angka yang terletak pada diagonal spiral angka ini adalah 101.
Berapakah jumlah angka-angka pada diagonal, jika dibentuk spiral dengan cara yang sama, namun berukuran 1001 x 1001?
Answer: 0d53425bd7c5bf9919df3718c8e49fa6
Soal 29
Jika kita mencoba menghitung semua kombinasi dari ab untuk 2 ≤ a ≤ 5 dan 2 ≤ b ≤ 5 maka kita akan mendapatkan:
22=4, 23=8, 24=16, 25=32
32=9, 33=27, 34=81, 35=243
42=16, 43=64, 44=256, 45=1024
52=25, 53=125, 54=625, 55=3125
Lalu jika kita urutkan angka-angka tersebut, dengan terlebih dahulu membuang angka yang berulang, maka kita akan mendapatkan barisan 15 buah bilangan berbeda sebagai berikut:
4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125
Berapakah banyak bilangan berbeda, pada barisan yang dibuat dari rumus ab untuk 2 ≤ a ≤ 100 dan 2 ≤ b ≤ 100?
Answer: 6f0ca67289d79eb35d19decbc0a08453
Soal 30
Hanya terdapat tiga buah bilangan yang jika digit-digitnya dipangkatkan empat, lalu dijumlahkan, akan menghasilkan angka yang sama:
1634 = 14 + 64 + 34 + 44
8208 = 84 + 24 + 04 + 84
9474 = 94 + 44 + 74 + 44
Tetapi 1 = 14 tidak ikut dimasukkan dalam bilangan-bilangan di atas, karena bukan merupakan hasil penjumlahan.
Jumlah dari semua bilangan tersebut adalah 1634 + 8208 + 9474 = 19316.
Carilah jumlah dari semua bilangan yang jika digit-digitnya dipangkatkan lima, lalu dijumlahkan, akan menghasilkan bilangan yang sama
Answer: 27a1779a8a8c323a307ac8a70bc4489d
Soal 31
Mata uang Inggris terdiri dari pecahan pound (£), dan pence (p), dan terdapat delapan macam koin yang beredar di sana:
1p, 2p, 5p, 10p, 20p, 50p, £1 (100p) dan £2 (200p).
Kita dapat membentuk £2 salah satunya dengan cara berikut:
1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p
Berapa banyak cara untuk membentuk £2 menggunakan koin yang beredar?
Answer: 142dfe4a33d624d2b830a9257e96726d
Soal 32
Kita dapat menyebut bilangan dengan n digit sebagai bilangan pandigital jika kita menggunakan semua digit dari 1 sampai n satu kali; sebagai contoh, bilangan 5 digit, 15234, adalah bilangan pandigital 1 sampai 5
7254 dapat ditulis sebagai hasil perkalian bilangan 39 × 186 = 7254, dan jika identitas ini dilihat dengan seksama, kita dapat menemukan semua angka dari 1 sampai 9. Identitas seperti ini dapat juga disebut pandigital.
Carilah jumlah dari semua bilangan, yang jika ditulis sebagai hasil kali, identitasnya dapat ditulis sebagai pandigital 1 sampai 9.
Answer: 100f6e37d0b0564490a2ee27eff0660d
Soal 33
Pecahan 49/98 adalah pecahan yang menarik, karena seseorang yang tidak paham matematika mungkin akan mencoba untuk menyederhanakan pecahan tersebut dengan menghapus angka yang sama, yaitu angka 9 pada pembilang dan penyebut 49/98 = 4/8, dan kebetulan hasilnya benar.
Pecahan angka puluhan seperti, 30/50 = 3/5, dapat kita sebut sebagai kasus trivial, dan tidak kita ikut sertakan pada perhitungan ini.
Hanya terdapat empat buah pecahan seperti ini yang tidak trivial, yang nilai desimalnya kurang dari satu, dan memiliki dua digit baik pada pembilang maupun penyebut
Jika hasil kali dari keempat pecahan ini diberikan dalam sampai yang bentuk yang paling sederhana, carilah nilai dari penyebutnya.
Answer: f899139df5e1059396431415e770c6dd
Soal 34
145 adalah bilangan yang menarik, karena 1! + 4! + 5! = 1 + 24 + 120 = 145.
Carilah jumlah semua bilangan yang jika faktorial dari semua digitnya dijumlahkan, hasilnya adalah bilangan yang sama.
Catatan: walaupun 1! = 1 dan 2! = 2, namun mereka tidak diikutsertakan karena bukan merupakan hasil penjumlahan beberapa faktorial digit.
Answer: 60803ea798a0c0dfb7f36397d8d4d772
Soal 35
Bilangan 197 dapat disebut bilangan prima siklik karena semua perputaran digitnya: 197, 971, dan 719, merupakan bilangan prima.
Terdapat tiga belas buah bilangan prima siklik yang lebih kecil daripada 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, dan 97.
Berapa banyak bilangan prima siklik yang lebih kecil dari satu juta?
Answer: b53b3a3d6ab90ce0268229151c9bde11
Soal 36
Bilangan desimal 585 = 10010010012 (biner), adalah bilangan palindrom, baik dalam basis 10 (desimal) ataupun basis 2 (biner).
Carilah jumlah dari semua bilangan, yang lebih kecil daripada satu juta, yang merupakan bilangan palindrom dalam basis 10 (desimal) dan dalam basis 2 (biner).
(Harap diingat, bahwa bilangan palindrom, dalam basis berapapun, tidak boleh diawali oleh angka nol.)
Answer: 0e175dc2f28833885f62e7345addff03
Soal 37
Bilangan 3797 memiliki sifat yang unik. Bilangan tersebut adalah prima, dan jika kita menghapus satu per satu digitnya dari kiri ke kanan, semua bilangan barunya tetaplah bilangan prima: 3797, 797, 97, dan 7. Kita dapat juga membuang digit dengan cara yang sama dari kanan ke kiri: 3797, 379, 37, dan 3, dan semua bilangan barunya juga tetaplah bilangan prima.
Hanya ada sebelas buah bilangan prima yang jika digitnya dihapus satu per satu baik dari kiri ke kanan maupun kanan ke kiri, tetap merupakan bilangan prima. Carilah jumlah kesebelas bilangan prima tersebut.
Catatan: 2, 3, 5, dan 7 tidak termasuk dalam kesebelas bilangan tersebut.
Answer: cace46c61b00de1b60874936a093981d
Soal 38
Ambil bilangan 192 dan kalikan dengan 1, 2, dan 3, akan didapat:
192 × 1 = 192
192 × 2 = 384
192 × 3 = 576
Dengan menyatukan semua hasil kali tersebut, kita akan mendapatkan bilangan pandigital 1 sampai 9, 192384576. Kita akan menyebut 192384576 sebagai hasil kali terangkaikan dari 192 dan (1,2,3)
Hasil yang serupa bisa didapatkan dengan angka 9 dan mengalikannya dengan 1, 2, 3, 4, dan 5, yang memberikan bilangan pandigital, 918273645, di mana bilangan ini merupakan hasil kali terangkaikan dari 9 dan (1,2,3,4,5).
Berapakah bilangan terbesar pandigital 1 sampai 9 yang dapat kita bentuk dari hasil kali terangkai suatu bilangan bulat dan (1,2, ... , n) di mana n > 1?
Answer: f2a29ede8dc9fae7926dc7a4357ac25e
Soal 39
Misalkan p adalah keliling dari sebuah segitiga siku-siku yang memiliki sisi {a,b,c}, dan a,b,dan c adalah bilangan bulat. Maka akan ada tiga buah segitiga untuk p = 120.
{20,48,52}, {24,45,51}, {30,40,50}
Berapakah nilai p ≤ 1000, yang akan menghasilkan jumlah segitiga siku-siku paling banyak?
Answer: fa83a11a198d5a7f0bf77a1987bcd006
Soal 40
Bentuk desimal dari sebuah pecahan irasional dibuat dengan merangkaikan barisan bilangan bulat positif:
0.123456789101112131415161718192021...
Dapat dilihat bahwa digit ke-12 di belakang koma adalah 1.
Jika dn melambangkan digit ke-n di belakang koma, carilah hasil dari bentuk berikut ini.
d1 × d10 × d100 × d1000 × d10000 × d100000 × d1000000
Answer: 6f3ef77ac0e3619e98159e9b6febf557
Soal 41
Kita dapat menyebut sebuah bilangan dengan n digit sebagai pandigital jika kita menggunakan semua digit dari 1 sampai n persis satu kali. Sebagai contoh, 2143 adalah bilangan pandigital 4 digit yang kebetulan juga merupakan bilangan prima.
Berapakah bilangan pandigital prima terbesar yang ada di dunia ini?
Answer: d0a1bd6ab4229b2d0754be8923431404
Soal 42
Suku ke-n dari barisan bilangan segitiga dapat dihitung sebagai tn = ½n(n+1); sehingga sepuluh bilangan segitiga pertama adalah:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
Dengan mengubah setiap huruf menjadi angka yang sesuai dengan urutan pada alfabet, dan menjumlahkan semua angka yang didapat untuk tiap kata, kita bisa mendapatkan nilai kata tersebut. Sebagai contoh, nilai dari kata SKY adalah 19 + 11 + 25 = 55 = t10. Jika nilai kata yang didapat termasuk dalam barisan bilangan segitiga, maka kata tersebut akan kita sebut sebagai kata segitiga
Menggunakan [words.txt](/projecteuler/files/words.txt) (klik kanan dan pilih 'Save Link/Target As...'), sebuah berkas berukuran 16K yang berisi kurang lebih dua ribu kata dalam bahasa Inggris, berapa banyak kata segitiga dalam berkas tersebut?
Answer: 82aa4b0af34c2313a562076992e50aa3
Soal 43
Bilangan 1406357289, adalah bilangan pandigital dari 0 sampai 9, karena bilangan ini memuat digit 0 sampai 9 tepat satu kali dengan urutan yang acak. Namun bilangan 1406357289 juga memiliki sifat lain yang cukup menarik, yaitu sifat habis dibaginya sub-string dari bilangan tersebut dengan bilangan prima.
Misalkan d1 adalah digit ke-1, d2 adalah digit ke-2, dan seterusnya. Dengan mengingat notasi ini, kita bisa menemukan bahwa:
- d2d3d4=406 habis dibagi 2
- d3d4d5=063 habis dibagi 3
- d4d5d6=635 habis dibagi 5
- d5d6d7=357 habis dibagi 7
- d6d7d8=572 habis dibagi 11
- d7d8d9=728 habis dibagi 13
- d8d9d10=289 habis dibagi 17
Carilah jumlah dari semua bilangan pandigital dari 0 sampai 9 yang memiliki sifat ini.
Answer: 115253b7721af0fdff25cd391dfc70cf
Soal 44
Bilangan segilima dapat dihitung dengan rumus sebagai berikut, Pn=n(3n−1)/2. Sepuluh bilangan segilima pertama adalah:
1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...
Dapat dilihat bahwa P4 + P7 = 22 + 70 = 92 = P8. Tetapi, selisih keduanya, 70 − 22 = 48, bukanlah bilangan segilima.
Carilah pasangan bilangan segilima, Pj dan Pk, di mana jumlah dan selisihnya juga merupakan bilangan segilima dengan nilai D = |Pk − Pj| paling kecil; berapakah nilai dari D?
Answer: 2c2556cb85621309ca647465ffa62370
Soal 45
Bilangan segitiga, segilima, dan segienam dapat dibentuk dari rumus berikut ini:
| Bilangan segitiga | Tn=n(n+1)/2 | 1, 3, 6, 10, 15, ... | ||
| Bilangan segilima | Pn=n(3n−1)/2 | 1, 5, 12, 22, 35, ... | ||
| Bilangan segienam | Hn=n(2n−1) | 1, 6, 15, 28, 45, ... |
Dapat dibuktikan bahwa T285 = P165 = H143 = 40755.
Carilah bilangan segitiga selanjutnya yang juga merupakan bilangan segilima dan segienam.
Answer: 30dfe3e3b286add9d12e493ca7be63fc
Soal 46
Christian Goldbach pernah mengajukan dugaan bahwa setiap bilangan ganjil yang bukan bilangan prima dapat dibentuk dari penjumlahan bilangan prima dengan kelipatan dua suatu bilangan kuadrat.
9 = 7 + 2×12
15 = 7 + 2×22
21 = 3 + 2×32
25 = 7 + 2×32
27 = 19 + 2×22
33 = 31 + 2×12
Namun ternyata dugaan ia salah.
Berapakah bilangan ganjil komposit (bukan bilangan prima) terkecil yang tidak bisa dituliskan sebagai hasil penjumlahan suatu bilangan prima dengan kelipatan dua suatu bilangan kuadrat?
Answer: 89abe98de6071178edb1b28901a8f459
Soal 47
Dua bilangan berurutan paling kecil yang memiliki faktor prima berbeda adalah:
14 = 2 × 7
15 = 3 × 5
Tiga bilangan berurutan paling kecil yang memiliki tiga faktor prima berbeda adalah:
644 = 2² × 7 × 23
645 = 3 × 5 × 43
646 = 2 × 17 × 19.
Carilah empat bilangan berurutan paling kecil yang memiliki empat faktor prima berbeda. Berapakah bilangan pertama dari keempat bilangan berurutan tersebut?
Answer: 748f517ecdc29106e2738f88aa7530f4
Soal 48
Deret 11 + 22 + 33 + ... + 1010 = 10405071317.
Carilah 10 digit terakhir dari jumlahan deret 11 + 22 + 33 + ... + 10001000.
Answer: 0829124724747ae1c65da8cae5263346
Soal 49
Suatu barisan aritmatika, 1487, 4817, 8147, yang tiap sukunya memiliki beda 3330, memiliki dua buah keunikan: (i) ketiga-tiganya adalah merupakan bilangan prima, dan, (ii) keempat digit pada setiap suku merupakan perubahan posisi/permutasi dari suku yang lain.
Tidak ada barisan aritmatika yang suku-sukunya merupakan bilangan prima satu, dua, atau tiga digit yang memiliki sifat di atas, namun masih ada satu lagi kelompok barisan aritmatika empat digit yang bisa memenuhi sifat di atas.
Jika ketiga suku dari barisan aritmatika tersebut dirangkaikan, maka akan terbentuk satu bilangan yang terdiri atas 12 digit. Berapakah bilangan tersebut?
Answer: 0b99933d3e2a9addccbb663d46cbb592
Soal 50
Bilangan prima 41, dapat dibentuk dari penjumlahan enam bilangan prima berurutan:
Ini adalah penjumlahan paling panjang bilangan prima berurutan yang jumlahnya menghasilkan bilangan prima kurang dari seratus.
Penjumlahan paling panjang bilangan prima berurutan yang hasilnya adalah bilangan prima kurang dari seribu membutuhkan 21 suku, dan hasilnya adalah 953.
Berapakah bilangan prima di bawah satu juta yang dapat dibentuk dari penjumlahan paling panjang bilangan prima berurutan?
Answer: 73229bab6c5dc1c7cf7a4fa123caf6bc
Soal 51
Dengan mengganti digit ke-1 dari bilangan 2 digit dengan bentuk *3, terdapat enam buah bilangan prima dari sembilan bilangan yang ada: 13, 23, 43, 53, 73, dan 83.
Dengan menukarkan digit ke-3 dan ke-4 dari bentuk bilangan 56**3 dengan digit yang sama, maka akan didapatkan sekumpulan bilangan 5 digit, dengan tujuh buah bilangan prima dari sepuluh kemungkinan bilangan yang ada: 56003, 56113, 56333, 56443, 56663, 56773, dan 56993. Dan 56003, me rupakan bilangan prima yang paling kecil dari kelompok ini.
Carilah bilangan prima yang paling kecil dari suatu kelompok, dimana kelompok tersebut didapatkan dengan mengganti beberapa bagian dari bil angan (tidak harus berurutan) dengan digit yang sama, dan kelompok tersebut memiliki delapan buah bilangan prima.
Answer: e2a8daa5eb919905dadd795593084c22
Soal 52
Dapat dilihat bahwa bilangan 125874, dan kelipatan duanya, 251748, mengandung digit-digit yang sama, namun dengan urutan yang berbeda.
Carilah bilangan bulat terkecil x, sedemikian rupa sehingga 2x, 3x, 4x, 5x, dan 6x mengandung digit-digit yang sama.
Answer: a420384997c8a1a93d5a84046117c2aa
Soal 53
Terdapat persis sepuluh cara untuk memilih tiga angka dari bilangan 12345:
123, 124, 125, 134, 135, 145, 234, 235, 245, and 345
Dalam kombinatorika, kita menggunakan lambang, 5C3 = 10.
Secara umum,
| nCr = | n! r!(n−r)! |
,dimana r ≤ n, n! = n×(n−1)×...×3×2×1, dan 0! = 1. |
Saat n = 23, nilai kombinasi yang ada akan melebihi satu juta: 23C10 = 1144066.
Berapa banyak kombinasi nCr yang akan menghasilkan nilai lebih dari satu juta, untuk n, 1 ≤ n ≤ 100? (Hasil kombinasi boleh sama)
Answer: e3b21256183cf7c2c7a66be163579d37
Soal 54
Dalam permainan kartu poker, seorang pemain bisa memegang lima kartu. Susunan kelima kartu tersebut dapat diperingkatkan, dari peringkat rendah ke peringkat tinggi dengan aturan sebagai berikut:
- High Card: Satu kartu yang memiliki nilai paling tinggi.
- One Pair: Satu pasang kartu yang memiliki nilai sama.
- Two Pairs: Terdapat dua One Pair berbeda.
- Three of a Kind: Tiga buah kartu yang memiliki nilai yang sama.
- Straight: Semua kartu memiliki nilai yang berurutan.
- Flush: Semua kartu memiliki suit (Spade, Heart, Diamond, Club) yang sama.
- Full House: Gabungan Three of a Kind dan One Pair.
- Four of a Kind: Empat kartu yang memiliki nilai yang sama.
- Straight Flush: Semua kartu memiliki nilai yang berurutan dan memiliki suit (Spade, Heart, Diamond, Club) yang sama.
- Royal Flush: Sepuluh, Jack, Queen, King, Ace, dalam suit (Spade, Heart, Diamond, Club) yang sama.
Semua kartu memiliki urutan nilai:
2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace.
Jika dua pemain memegang susunan kartu yang memiliki peringkat yang sama, maka kartu kedua pemain tersebut akan dibandingkan nilainya, yang memiliki nilai lebih besar menang; sebagai contoh, sepasang (One Pair) kartu delapan mengalahkan sepasang (One Pair) kartu lima. Namun apabila tidak bisa ditemukan nilai yang lebih besar, sebagai contoh, kedua pemain memiliki sepasang (One Pair) kartu queen, maka akan dilihat kartu sisanya, dan kartu sisa tersebut akan dibandingkan (lihat contoh 4 di bawah); Jika kartu dengan peringkat tertinggi dari kedua pemain ternyata seri, maka kartu peringkat selanjutnya yang akan dibandingkan, dan seterusnya.
Perhatikan kelima kartu yang dimiliki oleh dua pemain berikut:
| Permainan Ke | Pemain 1 | Pemain 2 | Pemenang | |||
| 1 | 5H 5C 6S 7S KD Sepasang (One Pair) kartu lima | 2C 3S 8S 8D TD Sepasang (One Pair) kartu delapan | Pemain 2 | |||
| 2 | 5D 8C 9S JS AC Kartu tertinggi (Highest Card) Ace | 2C 5C 7D 8S QH Kartu tertinggi (Highest Card) Queen | Pemain 1 | |||
| 3 | 2D 9C AS AH AC Tiga Aces (Three of a Kind) | 3D 6D 7D TD QD Flush dengan Diamonds | Pemain 2 | |||
| 4 | 4D 6S 9H QH QC Sepasang (One Pair) kartu Queen Kartu tertinggi (Highest Card) sembilan | 3D 6D 7H QD QS Sepasang (One Pair) kartu Queen Kartu tertinggi (Highest Card) tujuh | Pemain 1 | |||
| 5 | 2H 2D 4C 4D 4S Full House Dengan tiga buah kartu empat | 3C 3D 3S 9S 9D Full House Dengan tiga buah kartu tiga | Pemain 1 |
File, [poker.txt](/projecteuler/files/poker.txt), berisi seribu permainan acak yang dimainkan oleh dua orang pemain. Setiap baris dalam berkas berisi sepuluh kartu (yang dipisah oleh sebuah spasi): lima kartu pertama adalah milik pemain 1, dan lima kartu selanjutnya adalah milik pemain 2. Anda dapat mempercayai bahwa semua kartu yang ada sudah benar (tidak ada huruf yang salah diketik atau kartu ganda), Kartu pada setiap pemain dituliskan dengan urutan acak, dan dalam setiap permainan pasti ada pemenangnya.
Berapa kali pemain 1 menang?
Answer: 142949df56ea8ae0be8b5306971900a4
Soal 55
Jika kita memilih bilangan 47, lalu menjumlahkan dengan kebalikannya, 47 + 74 = 121, akan didapat hasil palindrom.
Namun cara ini tidak selalu langsung menghasilkan bilangan palindrom. Sebagai contoh,
349 + 943 = 1292,
1292 + 2921 = 4213
4213 + 3124 = 7337
Seperti contoh di atas, 349 memerlukan tiga iterasi dari cara di atas untuk mendapatkan bilangan palindrom.
Meskipun belum ada seorangpun yang membuktikannya, diduga bahwa ada beberapa bilangan, seperti 196, yang tidak bisa menghasilkan bilangan palindrom dengan cara di atas. Bilangan yang tidak dapat menghasilkan bilangan palindrom dengan cara menjumlahkan dengan kebalikannya disebut bilangan Lychrel.
Untuk keperluan penelitian ini, kita asumsikan bahwa semua bilangan adalah bilangan Lychrell, sampai bisa dibuktikan sebaliknya. Anggaplah bahwa untuk semua bilangan yang lebih kecil daripada sepuluh ribu, bilangan tersebut kemungkinan akan (i) menjadi bilangan palindrom setelah pengulangan proses (iterasi) kurang dari lima puluh kali, atau, (ii) kita tidak dapat menghasilkan bilangan palindrom, walaupun kita menggunakan segala kemampuan atau alat yang ada. Sebagai informasi, 10677 adalah bilangan pertama yang membutuhkan lebih dari lima puluh kali pengulangan agar dapat menghasilkan bilangan palindrom : 4668731596684224866951378664 (53 pengulangan, 28 angka).
Menariknya, ada beberapa bilangan palindrom yang juga merupakan bilangan Lychrel; contohnya 4994.
Berapa banyak bilangan Lychrel yang besarnya kurang dari sepuluh ribu?
Answer: 077e29b11be80ab57e1a2ecabb7da330
Soal 56
Satu googol (10100) adalah bilangan yang sangat besar: angka satu diikuti oleh seratus buah angka nol; 100100 juga merupakan bilangan yang bahkan lebih besar: angka satu diikuti oleh dua ratus buah angka nol. Namun walaupun berukuran besar, jumlah dari semua angkanya hanya 1.
Misalkan ada sebuah bilangan asli yang memiliki bentuk ab, di mana a, b < 100, berapakah jumlah terbesar dari angka-angka dalam ab?
Answer: c22abfa379f38b5b0411bc11fa9bf92f
Soal 57
Kita dapat menunjukkan bahwa akar dua dapat dinyatakan sebagai penjumlahan suatu pecahan sebanyak tak hingga kali.
√ 2 = 1 + 1/(2 + 1/(2 + 1/(2 + … ))) = 1.414213…
Dengan menghitung empat iterasi pertama dari rumus di atas, kita akan mendapat:
1 + 1/2 = 3/2 = 1.5
1 + 1/(2 + 1/2) = 7/5 = 1.4
1 + 1/(2 + 1/(2 + 1/2)) = 17/12 = 1.41666…
1 + 1/(2 + 1/(2 + 1/(2 + 1/2))) = 41/29 = 1.41379…
Tiga iterasi selanjutnya akan menghasilkan 99/70, 239/169, dan 577/408, Namun pada iterasi ke delapan, 1393/985, untuk pertama kalinya kita dap at menemukan banyaknya digit pada pembilang lebih banyak daripada pada penyebut.
Dalam seribu iterasi pertama, berapa banyak pecahan yang pembilangnya memiliki banyak digit yang lebih banyak dibanding penyebutnya?
Answer: b3e3e393c77e35a4a3f3cbd1e429b5dc
Soal 58
Dengan memulai menuliskan angka 1 di tengah, lalu berputar berlawanan arah jarum jam seperti pada bentuk berikut, kita dapat membentuk suatu spiral angka persegi dengan ukuran sisi 7.
37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49
Ada satu hal yang menarik, yaitu bilangan ganjil kuadrat tersusun di diagonal sebelah kanan bawah. Namun yang lebih menarik lagi, 8 dari 13 angka yang ada pada kedua diagonal adalah prima sehingga perbandingannya dapat dituliskan 8/13 ≈ 62%.
Jika satu lapis spiral lagi dibuat di sekeliling spiral di atas, maka kita akan mendapatkan spiral angka persegi dengan ukuran sisi 9. Jika proses ini dilanjutkan, berapakah panjang sisi terkecil dari persegi spiral angka seperti di atas, sehingga spiral tersebut memiliki perbandingan bilangan prima terhadap semua angka pada diagonal yang nilainya jatuh bawah 10%?
Answer: b62fc92a2561538525c89be63f36bf7b
Soal 59
Setiap karakter pada komputer disimpan dengan kode unik, dan salah satu standar konversi karakter tersebut adalah ASCII (American Standard Code for Information Interchange). Sebagai contoh, huruf A kapital memiliki kode A = 65, tanda bintang (*) = 42, dan huruf k kecil memiliki kode k = 107.
Proses enkripsi modern yang diterapkan pada suatu berkas, akan mengubah huruf ke kode ASCII-nya, lalu melakukan operasi XOR untuk setiap nilai yang didapat dengan nilai yang tertentu, yang diambil dari kunci rahasia. Keuntungan menggunakan metode XOR adalah kita dapat menggunakan kunci rahasia yang sama saat melakukan enkripsi untuk mengamankan teks, dan melakukan dekripsi kembali menjadi teks awal; sebagai contoh, 65 XOR 42 = 107, lalu 107 XOR 42 = 65.
Agar proses enkripsi tidak mudah ditembus, maka dibuatlah kunci rahasia yang sama panjang dengan teks awal, dan kunci ini dibentuk dari angka acak. Sang pengguna komputer akan menaruh pesan yang telah dienkripsi dan kunci rahasia tersebut di tempat yang berbeda, dan tanpa mengetahui keduanya, tidak memungkinkan untuk melakukan dekripsi pesan.
Sayangnya, metode ini tidak praktis untuk kebanyakan pengguna, sehingga metode ini disempurnakan dengan menggunakan kata sandi sebagai kunci rahasia. Jika kata sandi lebih pendek dari pesan yang ingin dikirim (dan sering kali terjadi demikian), maka kata sandi akan diulang terus menerus sampai sama panjang dengan pesan yang ingin dikirim. Keseimbangan dari metode ini adalah kita dapat menggunakan kata sandi yang cukup panjang, untuk berusaha mengamankan pesan yang ingin dikirim, namun yang masih memungkinkan untuk diingat.
Terdapat pesan rahasia yang ada di berkas cipher1.txt (klik kanan dan pilih ‘Save Link/Target As…’), berkas tersebut berisi pesan rahasia dalam bentuk kode ASCII. Tugas Anda akan dipermudah, yaitu dengan mengetahui bahwa kata sandi yang digunakan untuk enkripsi pesan ini adalah hanya terdiri dari tiga huruf kecil, dan pesan rahasia ini adalah sebuah pesan yang berisi kata berbahasa Inggris. Dekripsilah pesan tersebut, dan cari jumlah dari semua nilai ASCII pada pesan tersebut.
CATATAN: Enkripsi adalah proses mengubah pesan asli menjadi kode rahasia, Dekripsi adalah proses mengubah kembali kode rahasia menjadi pesan asli.
Answer: 68f891fe214e2bfa07c998ad5d0a390f
Soal 60
Bilangan prima 3, 7, 109, dan 674, sangat patut diperhatikan. Dengan mengambil dua dari empat buah bilangan prima tersebut, lalu merangkaikannya dengan susunan apapun, kita akan mendapatkan bilangan baru yang selalu prima. Sebagai contoh, ambil bilangan 7 dan 109, lalu rangkaikan. Keduanya baik 7109 maupun 1097 adalah bilangan prima. Jumlah dari ke empat bilangan prima di atas adalah 792, dan ini merupakan jumlah terkecil dari himpunan empat bilangan prima yang memiliki sifat seperti yang dijelaskan di atas.
Carilah jumlah terkecil dari himpunan lima bilangan prima, yang memiliki sifat bahwa bila dua bilangan primanya dirangkaikan, kita akan selalu mendapatkan bilangan prima.
Answer: a4b5a70ca8cf24d0eb4330748d1e72e5
Soal 61
Bilangan segitiga, segiempat, segilima, segienam, segitujuh, dan segidelapan adalah bilangan yang menggunakan nama segi banyak, dan bilangan tersebut dapat dibuat dengan rumus:
| Segitiga | P3,n=n(n+1)/2 | 1, 3, 6, 10, 15, ... | ||
| Segiempat | P4,n=n2 | 1, 4, 9, 16, 25, ... | ||
| Segilima | P5,n=n(3n−1)/2 | 1, 5, 12, 22, 35, ... | ||
| Segienam | P6,n=n(2n−1) | 1, 6, 15, 28, 45, ... | ||
| Segitujuh | P7,n=n(5n−3)/2 | 1, 7, 18, 34, 55, ... | ||
| Segidelapan | P8,n=n(3n−2) | 1, 8, 21, 40, 65, ... |
Sebuah himpunan dari tiga buah bilangan dengan 4 digit: 8128, 2882, 8281, memiliki tiga sifat yang menarik.
- Himpunan tersebut siklik, dua digit terakhir dari suatu bilangan adalah digit-digit awal dari bilangan selanjutnya (sifat ini juga berlaku untuk bilangan terakhir terhadap yang pertama).
- Semua bilangan pada himpunan di atas merupakan bilangan segibanyak yang berbeda: segitiga (P3,127=8128), segiempat (P4,91=8281), dan segilima (P5,44=2882).
- Himpunan ini adalah satu-satunya himpunan bilangan 4 angka yang memiliki kedua sifat di atas.
Carilah himpunan yang mirip seperti himpunan di atas, namun mengandung enam buah bilangan 4 angka, yang merupakan himpunan siklik, dan memiliki bilangan segitiga, segiempat, segilima, segienam, segitujuh, dan segidelapan yang berbeda.
Answer: caec17d84884addeec35c3610645ab63
Soal 62
Digit-digit pada bilangan kubik, 41063625 (3453), dapat diacak untuk membuat dua bilangan kubik lain: 56623104 (3843) dan 66430125 (4053). Faktanya, 41063625 adalah bilangan kubik terkecil yang memiliki tiga buah bilangan kubik, hasil pengacakan semua digitnya .
Carilah bilangan kubik terkecil, yang apabila digit-digitnya diacak, bisa menghasilkan lima bilangan kubik termasuk dengan bilangan itu sendiri.
Answer: 8f46b522b5401b8b6df99a7410eea44b
Soal 63
Sebuah bilangan dengan 5 digit, 16807=75, juga merupakan hasil pangkat lima suatu bilangan lain. Hal yang serupa, bilangan 9 digit, 134217728=89, adalah hasil pangkat sembilan suatu bilangan lain.
Berapa banyak bilangan positif n-digit, yang juga merupakan hasil pangkat n suatu bilangan?
Answer: f457c545a9ded88f18ecee47145a72c0
Soal 64
Semua akar kuadrat adalah periodik (berulang) saat ditulis dalam pecahan kontinu seperti berikut ini:
| √N = a0 + | 1 |
||
| a1 + | 1 |
||
| a2 + | 1 |
||
| a3 + ... | |||
Sebagai contoh, perhatikan √23:
| √23 = 4 + √23 — 4 = 4 + | 1 |
= 4 + | 1 |
|
1 √23—4 |
1 + | √23 – 3 7 |
||
Jika kita melanjutkannya, maka kita akan mendapatkan bentuk sebagai berikut:
| √23 = 4 + | 1 |
|||
| 1 + | 1 |
|||
| 3 + | 1 |
|||
| 1 + | 1 |
|||
| 8 + ... | ||||
Dan proses di atas dapat dituliskan sebagai berikut:
| a0 = 4, | 1 √23—4 |
= | √23+4 7 |
= 1 + | √23—3 7 |
|
| a1 = 1, | 7 √23—3 |
= | 7(√23+3) 14 |
= 3 + | √23—3 2 |
|
| a2 = 3, | 2 √23—3 |
= | 2(√23+3) 14 |
= 1 + | √23—4 7 |
|
| a3 = 1, | 7 √23—4 |
= | 7(√23+4) 7 |
= 8 + | √23—4 | |
| a4 = 8, | 1 √23—4 |
= | √23+4 7 |
= 1 + | √23—3 7 |
|
| a5 = 1, | 7 √23—3 |
= | 7(√23+3) 14 |
= 3 + | √23—3 2 |
|
| a6 = 3, | 2 √23—3 |
= | 2(√23+3) 14 |
= 1 + | √23—4 7 |
|
| a7 = 1, | 7 √23—4 |
= | 7(√23+4) 7 |
= 8 + | √23—4 |
Kita dapat menemukan bahwa terdapat pola berulang. Untuk memudahkan, kita gunakan lambang √23 = [4;(1,3,1,8)], untuk memberitahu bahwa blok (1,3,1,8) berulang sampai tak hingga kali
Sepuluh representasi pecahan kontinu dari bilangan akar kuadrat (bilangan irasional) adalah:
√2=[1;(2)], periode=1
√3=[1;(1,2)], periode=2
√5=[2;(4)], periode=1
√6=[2;(2,4)], periode=2
√7=[2;(1,1,1,4)], periode=4
√8=[2;(1,4)], periode=2
√10=[3;(6)], periode=1
√11=[3;(3,6)], periode=2
√12= [3;(2,6)], periode=2
√13=[3;(1,1,1,1,6)], periode=5
Terdapat persis empat buah dari bentuk di atas, untuk N ≤ 13, yang memiliki periode ganjil.
Berapakah banyaknya bentuk di atas, untuk N ≤ 10000 yang memiliki periode ganjil?
Answer: dc960c46c38bd16e953d97cdeefdbc68
Soal 65
Akar kuadrat dari 2 dapat ditulis sebagai pecahan kontinu.
| √2 = 1 + | 1 |
|||
| 2 + | 1 |
|||
| 2 + | 1 |
|||
| 2 + | 1 |
|||
| 2 + ... | ||||
Pecahan kontinu tersebut dapat ditulis, √2 = [1;(2)], (2) menandakan bahwa 2 berulang secara ad infinitum (sampai tak hingga kali). Dengan proses yang sama, √23 = [4;(1,3,1,8)].
Ternyata teknik perhitungan akar kuadrat ini memberikan hasil rasional yang sangat mendekati nilai aslinya. Sebagai contoh kita akan melihat √2.
| 1 + | 1 |
= 3/2 |
2 |
| 1 + | 1 |
= 7/5 | |
| 2 + | 1 |
||
2 |
|||
| 1 + | 1 |
= 17/12 | ||
| 2 + | 1 |
|||
| 2 + | 1 |
|||
2 |
||||
| 1 + | 1 |
= 41/29 | |||
| 2 + | 1 |
||||
| 2 + | 1 |
||||
| 2 + | 1 |
||||
2 |
|||||
Barisan dari sepuluh bilangan pertama yang konvergen ke √2 adalah:
Yang mengejutkan, sebuah konstanta penting dalam matematika dapat juga dinyatakan dalam blok berulang, yaitu
e = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...].
Sepuluh bentuk pecahan pertama yang konvergen kek e adalah:
Jumlah semua angka pada bilangan pembilang pecahan ke-10 adalah 1+4+5+7=17.
Carilah jumlah semua angka pada bilangan pembilang pecahan ke-100, dari pecahan kontinu yang konvergen ke e.
Answer: 7a614fd06c325499f1680b9896beedeb
Soal 66
Perhatikan sebuah persamaan kuadrat Diophantine sebagai berikut:
x2 – Dy2 = 1
Saat D=13, solusi minimal x adalah 6492 – 13×1802 = 1.
Kita dapat asumsikan bahwa tidak ada solusi bilangan bulat positif ketika D merupakan bilangan kuadrat.
Dengan mencari solusi minimal x untuk D = {2, 3, 5, 6, 7}, kita akan mendapatkan hasil sebagai berikut:
32 – 2×22 = 1
22 – 3×12 = 1
92 – 5×42 = 1
52 – 6×22 = 1
82 – 7×32 = 1
Dapat kita lihat solusi minimal x di atas untuk D ≤ 7, hasil x terbesar kita dapatkan saat D=5.
Carilah nilai D ≤ 1000, yang solusi minimal x nya merupakan solusi x terbesar.
Answer: 3a066bda8c96b9478bb0512f0a43028c
Soal 67
Dengan dimulai dari sisi atas segitiga seperti gambar berikut, dan berpindah ke angka sebelah kiri atau kanan pada baris di bawahnya, maka akan didapat bahwa jumlah bilangan maksimum dari atas sampai bawah adalah 23.
3
7 4
2 4 6
8 5 9 3
Jumlahnya, 3 + 7 + 4 + 9 = 23.
Carilah jumlah bilangan maksimum dengan cara serupa di atas, dari atas ke bawah pada segitiga [triangle.txt](/projecteuler/files/triangle.txt) (Klik kanan dan pilih 'Save Link/Target As...'), triangle.txt adalah sebuah berkas teks 15K yang memuat segitiga mirip seperti di atas sebanyak seratus baris.
NOTE: Ini adalah versi lebih sulit dari [Soal 18](#problem-18). Kita tidak dapat menyelesaikan masalah ini dengan mencoba melakukan perhitungan pada jalur satu per satu, karena terdapat 299 kemungkinan jalur! Bahkan jika anda dapat memeriksa satu triliun (1012) rute per detik pun, anda memerlukan lebih dari dua puluh miliar tahun untuk memeriksa semuanya. Terdapat cara yang efisien untuk menyelesaikan masalah ini. ;o)
Answer: 9d702ffd99ad9c70ac37e506facc8c38
Soal 68
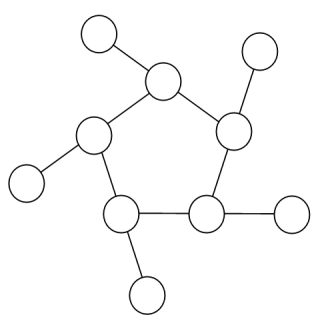
Perhatikan sebuah cincin 3-gon "ajaib" , berisi angka dari 1 sampai 6. Setiap angka pada satu garis lurus akan berjumlah sembilan.

Dengan melihat garis yang titik luar dengan angka terkecil (4,3,2 pada contoh ini), lalu melihat berputar searah jarum jam, setiap gambar akan menghasilkan solusi unik. sebagai contoh, solusi dari bentuk di atas dapat dideskripsikan oleh himpunan: 4,3,2; 6,2,1; 5,1,3.
Cincin di atas dapat dibuat dengan berbagai jumlah angka dalam satu garis lurus, yaitu: 9, 10, 11, and 12. Terdapat sebanyak delapan solusi untuk cincin di atas.
| Jumlah Angka | Himpunan Solusi |
| 9 | 4,2,3; 5,3,1; 6,1,2 |
| 9 | 4,3,2; 6,2,1; 5,1,3 |
| 10 | 2,3,5; 4,5,1; 6,1,3 |
| 10 | 2,5,3; 6,3,1; 4,1,5 |
| 11 | 1,4,6; 3,6,2; 5,2,4 |
| 11 | 1,6,4; 5,4,2; 3,2,6 |
| 12 | 1,5,6; 2,6,4; 3,4,5 |
| 12 | 1,6,5; 3,5,4; 2,4,6 |
Dengan merangkaikan setiap himpunan, kita bisa mendapatkan bilangan dengan 9 angka; dan angka terbesar untuk cincin 3-gon adalah 432621513.
Dengan menggunakan angka dari 1 sampai 10, dan dengan mencoba berbagai macam susunan, kita dapat membuat bilangan dengan 16 atau 17 angka. Berapakah bilangan dengan 16 angka terbesar yang dapat dibentuk dari cincin 5-gon "ajaib"?
Answer: 26227442c6fed0292a528ac3790175be
Soal 69
Fungsi Totient Euler, φ(n) [terkadang disebut fungsi phi], digunakan untuk menentukan banyaknya bilangan yang lebih kecil dari n, dan juga relatif prima terhadap n. Sebagai contoh, 1, 2, 4, 5, 7, dan 8, adalah semua angka yang kurang dari sembilan, dan relatif prima terhadap sembilan, φ(9)=6.
| n | Relatif Prima | φ(n) | n/φ(n) |
| 2 | 1 | 1 | 2 |
| 3 | 1,2 | 2 | 1.5 |
| 4 | 1,3 | 2 | 2 |
| 5 | 1,2,3,4 | 4 | 1.25 |
| 6 | 1,5 | 2 | 3 |
| 7 | 1,2,3,4,5,6 | 6 | 1.1666... |
| 8 | 1,3,5,7 | 4 | 2 |
| 9 | 1,2,4,5,7,8 | 6 | 1.5 |
| 10 | 1,3,7,9 | 4 | 2.5 |
Dapat kita lihat, bahwa saat n=6 kita mendapatkan nilai n/φ(n) terbesar, untuk n ≤ 10.
Carilah nilai dari n ≤ 1,000,000 dimana nilai n/φ(n) merupakan yang terbesar.
Catatan: Dua bilangan a dan b disebut relatif prima jika FPB(a,b)=1
Answer: bf08b01ead83cbd62a9839ca1cf35ada
Soal 70
Fungsi Totient Euler, φ(n) [terkadang disebut fungsi phi], digunakan untuk menentukan banyaknya bilangan yang lebih kecil dari n, dan juga relatif prima terhadap n. Sebagai contoh, 1, 2, 4, 5, 7, dan 8, adalah semua angka yang kurang dari sembilan, dan relatif prima terhadap sembilan, φ(9)=6.
Angka 1 dianggap relatif prima ke semua bilangan positif, sehingga φ(1)=1.
Yang menarik, φ(87109)=79180, dan dapat kita lihat bahwa bilangan 87109 merupakan permutasi dari 79180.
Carilah nilai dari n, 1 < n < 107, di mana φ(n) merupakan permutasi dari n dan rasionya n/φ(n) menghasilkan nilai terkecil.
Answer: 1884dde67ced589082c8b7043abce181
Soal 71
Misalkan suatu pecahan n/d, di mana n dan d adalah bilangan bulat positif. Jika n<d dan FPB(n,d)=1, maka pecahan tersebut dapat disebut pecahan paling sederhana.
Jika kita membuat daftar semua pecahan yang paling sederhana untuk d ≤ 8 dari yang bernilai paling kecil ke paling besar, maka kita akan mendapatkan:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
Dapat kita lihat bahwa 2/5 muncul persis di sebelah kiri dari 3/7.
Dengan membuat daftar semua pecahan paling sederhana untuk d ≤ 1.000.000 dari yang bernilai paling kecil ke paling besar, carilah pembilang yang persis ada di sebelah kiri dari 3/7.
Answer: 71f38fa2f04db30be52f883d583bfd6f
Soal 72
Misalkan suatu pecahan, n/d, dimana n dan d adalah bilangan bulat positif. Jika n<d dan FPB(n,d)=1, maka pecahan tersebut dapat disebut pecahan paling sederhana.
Jika kita membuat daftar semua pecahan yang paling sederhana untuk d ≤ 8 dari yang bernilai paling kecil ke paling besar, maka kita akan mendapatkan:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
Dapat kita lihat bahwa terdapat 21 buah suku dalam barisan ini.
Berapa banyak elemen yang ada dalam himpunan semua pecahan yang paling sederhana untuk d ≤ 1,000,000?
Answer: 0384fb529dc651fe0f460acff3e9ac5d
Soal 73
Misalkan suatu pecahan, n/d, dimana n dan d adalah bilangan bulat positif. Jika n<d dan FPB(n,d)=1, maka pecahan tersebut dapat disebut pecahan paling sederhana.
Jika kita membuat daftar semua pecahan yang paling sederhana untuk d ≤ 8 dari yang bernilai paling kecil ke paling besar, maka kita akan mendapatkan:
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
Dapat kita lihat bahwa terdapat 3 pecahan lain antara 1/3 dan 1/2.
Berapa banyak pecahan yang terdapat antara 1/3 dan 1/2, dalam himpunan terurut semua pecahan yang paling sederhana untuk d ≤ 12,000?
Answer: 990a49eb474672444137fff1e5528a1b
Soal 74
Bilangan 145 dikenal karena sifatnya yang menarik, yaitu jumlah faktorial dari semua digitnya juga sama dengan 145:
1! + 4! + 5! = 1 + 24 + 120 = 145
Namun jika dihitung dengan cara serupa seperti di atas, sifat ini tidak langsung terlihat pada angka 169. Bahkan bilangan 169 menciptakan rantai terpanjang yang akan kembali ke 169; ternyata hanya terdapat tiga buah rantai (loop) yang bisa kembali ke angka awalnya:
169 → 363601 → 1454 → 169
871 → 45361 → 871
872 → 45362 → 872
Tidaklah sulit untuk membuktikan bahwa bilangan-bilangan lain akan memiliki rantai yang tidak kembali ke awal, jika dihitung dengan cara serupa di atas. Sebagai contoh,
69 → 363600 → 1454 → 169 → 363601 (→ 1454)
78 → 45360 → 871 → 45361 (→ 871)
540 → 145 (→ 145)
Jika rantai dibuat dengan angka awal 69, maka kita akan mendapatkan rantai yang berisi lima suku tidak berulang, dan diketahui bahwa rantai tidak berulang terpanjang yang dapat dibuat, dengan bilangan awal yang lebih kecil dari dari satu juta, memiliki enam puluh suku.
Berapa banyak rantai, dengan angka awal lebih kecil dari satu juta, yang memiliki persis enam puluh suku tidak berulang?
Answer: 69cb3ea317a32c4e6143e665fdb20b14
Soal 75
Diketahui bahwa 12 cm adalah panjang kawat terpendek yang bisa ditekuk untuk membentuk segitiga siku-siku yang sisi-sisinya merupakan bilangan bulat. Berikut ini adalah beberapa contoh dari kawat lain.
12 cm: (3,4,5)
24 cm: (6,8,10)
30 cm: (5,12,13)
36 cm: (9,12,15)
40 cm: (8,15,17)
48 cm: (12,16,20)
Ada beberapa kawat, seperti yang memiliki panjang 20 cm, yang tidak bisa ditekuk untuk membentuk segitiga siku-siku yang panjang sisi-sisinya berupa bilangan bulat. Sementara itu beberapa kawat lainnya memungkinkan untuk ditekuk menjadi lebih dari satu macam segitiga siku-siku yang panjang sisi-sisinya berupa bilangan bulat; sebagai contoh, kawat sepanjang 120 cm memungkinkan untuk dibuat menjadi tiga macam segitiga siku-siku yang panjang sisinya berupa bilangan bulat.
120 cm: (30,40,50), (20,48,52), (24,45,51)
Diketahui L adalah panjang kawat. Berapakah banyak kawat dengan L ≤ 1,500,000 yang dapat membentuk persis satu buah segitiga siku-siku, yang panjang sisi-sisinya merupakan bilangan bulat?
Answer: 583e391a7bd87f785412f72f486433cb
Soal 76
Kita dapat menuliskan lima sebagai hasil penjumlahan bilangan-bilangan lain dengan enam cara:
4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1
Berapakah banyaknya cara bilangan seratus ditulis sebagai hasil penjumlahan bilangan-bilangan lainnya?
Answer: 18ed0f01e082beffe0049ae1272689d2
Soal 77
Kita dapat menuliskan sepuluh sebagai hasil penjumlahan bilangan-bilangan prima dengan lima cara:
7 + 3
5 + 5
5 + 3 + 2
3 + 3 + 2 + 2
2 + 2 + 2 + 2 + 2
Berapakah bilangan terkecil yang dapat dituliskan sebagai jumlahan bilangan-bilangan prima dalam lebih dari lima ribu macam cara berbeda?
Answer: e2c420d928d4bf8ce0ff2ec19b371514
Soal 78
Misalkan p(n) adalah banyaknya cara mengelompokkan n buah koin. Sebagai contoh, lima koin dapat dikelompokkan dalam tujuh cara yang berbeda, sehingga p(5)=7.
| OOOOO |
| OOOO O |
| OOO OO |
| OOO O O |
| OO OO O |
| OO O O O |
| O O O O O |
Carilah nilai terkecil dari n, bila p(n) habis dibagi oleh satu juta.
Answer: ef2a8695e428116131cc94c651d0e566
Soal 79
Teknik pengamanan yang umum digunakan untuk perbankan daring (online banking) adalah dengan cara menanyakan pengguna tiga karakter acak dari sandi nasabah itu. Sebagai contoh jika sandi yang digunakan adalah 531278, bank bisa menanyakan angka ke-2, ke-3, dan ke-5; sehingga jawaban yang diharapkan oleh bank adalah: 317.
Sebuah berkas teks, [keylog.txt](/projecteuler/files/keylog.txt), berisi lima puluh proses login yang berhasil dari seorang nasabah bank.
Diketahui bahwa tiga karakter yang diminta oleh bank selalu diambil secara berurutan dari kiri ke kanan (contoh : bank tidak bisa mengambil angka ke-2, ke-9, lalu ke-3, karena angka ke-9 harusnya diambil terakhir). Analisislah berkas tersebut, dan tentukan sandi yang paling pendek yang mungkin digunakan oleh nasabah tersebut.
Answer: 3ccc6e16d99b21d42948f6d49b90fa30
Soal 80
Kita ketahui bahwa bila hasil akar kuadrat dari bilangan asli bukan merupakan bilangan bulat, maka akar kuadrat itu adalah bilangan irasional. Bentuk desimal dari akar kuadrat ini akan terus berlanjut tanpa ada pola yang berulang.
Akar kuadrat dari dua adalah 1,41421356237309504880…, dan penjumlahan dari seratus buah angka yang terletak di belakang koma adalah 475.
Untuk seratus bilangan asli pertama, carilah jumlah dari seratus buah angka-angkanya yang terletak di belakang koma, hanya untuk akar kuadrat yang irasional.
Answer: 6cc501a25298e4051886ef1a126e9484
Soal 81
Pada matriks ukuran 5 x 5 berikut ini, misalkan kita menelusuri jalur yang dimulai dari ujung kiri atas, ke ujung kanan bawah. Saat menelusuri jalur kita hanya dapat berpindah ke kanan dan bawah. Jalur yang memiliki hasil penjumlahan angka-angka terkecil ditandai dengan warna merah, dan jumlahnya sama dengan 2427.
Carilah jalur yang memiliki jumlah angka-angka terkecil, pada [matrix.txt](/projecteuler/files/matrix.txt) (klik kanan dan pilih "Save Link/Target As..."), sebuah berkas teks berukuran 31K yang berisi matriks berukuran 80 x 80. Jalur harus dimulai dari ujung kiri atas, dan bergerak menuju ujung kanan bawah, serta hanya diperbolehkan untuk berpindah ke kanan dan ke bawah.
Answer: f9ffec84499832add77e6a8bb00246ec
Soal 82
CATATAN: Soal ini adalah versi yang lebih menantang dari [Soal 81](#soal-81).
Jalur yang memiliki hasil penjumlahan angka-angka terkecil, pada matriks ukuran 5 x 5 berikut ini, ditandai dengan angka berwarna merah; jumlahnya adalah 994. Jalur dapat dimulai di manapun pada kolom paling kiri, dan harus berakhir di manapun pada kolom paling kanan, dan hanya diperbolehkan untuk bergeser ke atas, bawah, dan kanan.
Carilah jalur dengan hasil penjumlahan angka-angka terkecil, pada [matrix.txt](/projecteuler/files/matrix.txt) (klik kanan dan pilih "Save Link/Target As..."), sebuah berkas teks berukuran 31K yang berisi matriks berukuran 80 x 80. Jalur harus dimulai dari kolom paling kiri ke kolom paling kanan.
Answer: e6b3b1cd89b018d4754cf63863f6690a
Soal 83
CATATAN: Soal ini adalah versi yang jauh lebih menantang dari [Soal 81](#soal-81).
Pada matriks ukuran 5 x 5 berikut ini, jalur yang memiliki hasil penjumlahan angka-angka terkecil, dimulai dari pojok kiri atas, ke pojok kanan bawah, denagn bergerak ke kiri, kanan, atas, dan bawah, ditandai oleh angka berwarna merah, dan jumlahnya adalah 2297.
Carilah jalur yang memiliki hasil penjumlahan angka-angka terkecil, pada [matrix.txt](/projecteuler/files/matrix.txt) (klik kanan dan pilih "Save Link/Target As..."), sebuah berkas teks berukuran 31K yang berisi matriks berukuran 80 x 80. Jalur harus dimulai dari ujung kiri atas, ke ujung kanan bawah, dengan bergerak ke kiri, kanan, atas, dan bawah.
Answer: 61b28c4fbe8560003ee50fa5619d7a1e
Soal 84
Dalam permainan Monopoly, papan permainan standar yang digunakan adalah sebagai berikut:
| GO | A1 | CC1 | A2 | T1 | R1 | B1 | CH1 | B2 | B3 | PENJARA |
| H2 | C1 | |||||||||
| T2 | U1 | |||||||||
| H1 | C2 | |||||||||
| CH3 | C3 | |||||||||
| R4 | R2 | |||||||||
| G3 | D1 | |||||||||
| CC3 | CC2 | |||||||||
| G2 | D2 | |||||||||
| G1 | D3 | |||||||||
| G2J | F3 | U2 | F2 | F1 | R3 | E3 | E2 | CH2 | E1 | FP |
Seorang pemain mulai dari petak GO, lalu jumlah dari dua buah dadu bermuka enam yang dilemparkan akan menjadi jumlah petak yang harus dilalui oleh pemain tersebut. Petak-petak harus dilalui searah jarum jam. Kita dapat mengunjungi semua petak dengan probabilitas yang sama, yaitu: 2.5%. Tetapi, berada di G2J (Go To Jail/Masuk Penjara), CC (community chest/dana umum), dan CH (chance/kesempatan) akan membuat peluang berubah.
Selain G2J, dan satu kartu dari CC serta CH, ada cara lain yang bisa membuat pemain untuk masuk PENJARA, yaitu jika pemain tiga kali berturut-turut memperoleh dadu yang kedua angkanya sama, mereka tidak maju pada putaran dadu ketiga, tetapi mereka langsung menuju ke kotak PENJARA.
Saat memulai permainan, tumpukan kartu CC dan CH diacak. Saat pemain sampai di kotak CC atau CH, ia akan mengambil satu kartu paling atas dari tumpukan yang sesuai, lalu setelah mengikuti petunjuk yang tertera pada kartu, kartu dikembalikan ke tumpukan yang paling bawah. Terdapat enam belas kartu dalam setiap tumpukan, namun dalam soal ini, kita hanya mempedulikan kartu yang bisa mempengaruhi perpindahan petak dari pemain; segala kartu yang isinya tidak berkaitan dengan perpindahan petak, tidak akan dipedulikan, dan pemain akan tetap berada di petak CC/CH.
- Community Chest/Dana Umum (2/16 kartu):
- Pindah ke kotak GO
- Masuk ke PENJARA
- Chance/Kesempatan (10/16 cards):
- Pindah ke petak GO
- Masuk ke PENJARA
- Pindah ke petak C1
- Pindah ke petak E3
- Pindah ke petak H2
- Pindah ke petak R1
- Pindah ke petak R selanjutnya (milik perusahaan kereta api/railway)
- Pindah ke petak R selanjutnya
- Pindah ke petak U selanjutnya (milik perusahaan listrik dan air)
- Mundur 3 petak.
Masalah utama dari soal ini berkaitan dengan kemungkinan untuk mengunjungi petak tertentu setelah melakukan putaran dadu. Perlu dijelaskan, bahwa dengan mengabaikan petak G2J, karena petak ini tidak mungkin menjadi petak yang ditempati setelah pemain memutar dadu, sehingga petak G2J akan mempunyai probabilitas nol untuk disinggahi setelah dadu diputar. Petak CH akan memiliki peluang paling kecil untuk ditempati, karena 10 dari 16 kartu pada chance/kesempatan akan membuat pemain pindah ke petak lain, dan kita hanya akan menghitung posisi paling akhir dari setiap putaran dadu pemain. Kita tidak akan membuat perbedaan antara "hanya sekedar lewat" dengan masuk ke PENJARA, dan kita juga akan mengabaikan aturan yang mengharuskan pemain memiliki dadu kembar untuk "keluar dari penjara", dengan asumsi semua pemain pasti membayar untuk keluar dari penjara.
Dengan memulai dari petak GO, lalu memberi nomor untuk setiap petak secara berurutan dari 00 ke 39, kita dapat merangkaikan bilangan dua digit tersebut, untuk membentuk untai yang akan melambangkan petak-petak yang telah dikunjungi.
Secara statistik, dapat ditunjukan tiga petak yang paling populer dikunjungi. Secara berurutan petak tersebut adalah, PENJARA (6.24%) = petak ke-10, E3 (3.18%) = petak ke-24, dan petak GO (3.09%) = petak ke-00. Sehingga ketiga petak yang paling sering dikunjungi tersebut dapat ditulis dengan bilangan enam digit: 102400.
Jika kita tidak menggunakan dadu bermuka enam, dan kedua dadu diganti menjadi dadu bermuka empat, carilah bilangan enam digit yang melambangkan kotak yang paling sering dikunjungi seperti di atas.
Answer: ead3264438ef83a8c2da2e98067b4445
Soal 85
Dengan menghitung secara teliti, dapat terlihat bahwa terdapat delapan belas segi empat, pada kisi berukuran 3 x 2:
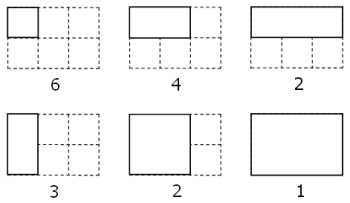
Tidak ada kisi yang bisa menghasilkan persis dua juta segi empat. Namun carilah ukuran kisi yang bisa menghasilkan segi empat mendekati dua juta buah, lalu hitunglah luas kisi tersebut.
Answer: 92bf5e6240737e0326ea59846a83e076
Soal 86
Seekor laba-laba ditandai dengan huruf S, berada pada salah satu pojok ruangan berbentuk balok, dengan ukuran 6 x 5 x 3, dan seekor lalat ditandai dengan huruf F, berada di pojok seberangnya. Dengan berjalan pada permukaan ruangan, panjang jalur terpendek yang berupa "garis lurus" dari S ke F adalah 10, dan jalurnya ditunjukkan pada gambar.
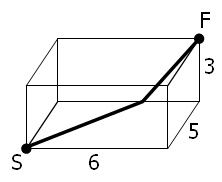
Terdapat sampai tiga pilihan jalur terpendek untuk setiap balok, dan jalur terpendek dari pilihan tersebut terkadang bukanlah merupakan bilangan bulat.
Jika rotasi dari balok diabaikan, bisa ditunjukkan bahwa ada 2060 balok berbeda, untuk balok yang memiliki panjang sisi berupa bilangan bulat berukuran maksimum M x M x M (semua jalur terpendek adalah bilangan bulat), untuk M = 100. Ini adalah nilai M paling kecil, yang bisa menghasilkan jalur terpendek berupa bilangan bulat lebih besar dari dua ribu buah; jumlah jalur terpendek saat M = 99 adalah 1975.
Carilah nilai M terkecil sehingga jumlah jalur terpendek yang ada banyaknya melebihi satu juta (jalur harus berupa bilangan bulat).
Answer: f5c3dd7514bf620a1b85450d2ae374b1
Soal 87
Bilangan terkecil yang dapat dituliskan sebagai hasil penjumlahan kuadrat bilangan prima, pangkat tiga bilangan prima, dan pangkat empat bilangan prima adalah 28. Dan hanya terdapat persis empat bilangan kurang dari lima puluh yang bisa dituliskan dengan cara di atas:
28 = 22 + 23 + 24
33 = 32 + 23 + 24
49 = 52 + 23 + 24
47 = 22 + 33 + 24
Berapa banyak bilangan yang lebih kecil dari lima puluh juta, yang bisa dituliskan sebagai hasil penjumlahan kuadrat bilangan prima, pangkat tiga bilangan prima, dan pangkat empat bilangan prima?
Answer: e7fb7907f1af626cc42e787e367ec602
Soal 88
Sebuah bilangan asli N, yang dapat ditulis sebagai hasil penjumlahan dan perkalian dari himpunan bilangan asli lain, {a1, a2, ... , ak} disebut bilangan hasilkali-jumlahan: N = a1 + a2 + ... + ak = a1 × a2 × ... × ak.
Sebagai contoh, 6 = 1 + 2 + 3 = 1 × 2 × 3.
Jika banyaknya bilangan asli lain yang bisa digunakan adalah k, kita harus mencari bilangan N terkecil yang bisa memenuhi sifat hasilkali-jumlahan. Bilangan hasilkali-jumlahan terkecil untuk nilai k = 2, 3, 4, 5, dan 6 adalah sebagai berikut.
k=2: 4 = 2 × 2 = 2 + 2
k=3: 6 = 1 × 2 × 3 = 1 + 2 + 3
k=4: 8 = 1 × 1 × 2 × 4 = 1 + 1 + 2 + 4
k=5: 8 = 1 × 1 × 2 × 2 × 2 = 1 + 1 + 2 + 2 + 2
k=6: 12 = 1 × 1 × 1 × 1 × 2 × 6 = 1 + 1 + 1 + 1 + 2 + 6
Kemudian untuk 2≤k≤6, jumlah semua bilangan hasilkali-jumlahan terkecilnya adalah 4+6+8+12 = 30; perhatikan bahwa 8 hanya dihitung sekali dalam penjumlahan tersebut.
Contoh lainnya, himpunan bilangan hasilkali-jumlahan terkecil untuk 2≤k≤12 adalah {4, 6, 8, 12, 15, 16}, dan jumlahnya adalah 61.
Berapakah hasil penjumlahan semua bilangan hasilkali-jumlahan terkecil untuk 2≤k≤12000?
Answer: ffde7251f43906d31534ae69fa555757
Soal 89
Sebuah bilangan Romawi dapat dianggap sahih apabila mengikuti beberapa aturan dasar. Walaupun mungkin aturan tersebut akan membuat beberapa bilangan dapat ditulis dengan lebih dari satu cara, namun pasti terdapat cara penulisan "terbaik" dari bilangan tersebut.
Sebagai contoh, terdapat setidaknya enam cara untuk menulis angka enam belas:
IIIIIIIIIIIIIIII
VIIIIIIIIIII
VVIIIIII
XIIIIII
VVVI
XVI
Tetapi, berdasarkan aturan, hanya XIIIIII dan XVI yang valid, dan XVI dianggap sebagai cara penulisan yang paling efisien, karena cara penulisan ini menggunakan huruf yang paling sedikit.
Sebuah berkas teks berukuran 11K, [roman.txt](/projecteuler/files/roman.txt), berisi seribu bilangan Romawi yang sahih, tetapi belum tentu paling efisien, lihat (see [About Roman Numerals](/projecteuler/files/about_roman_numerals.txt) untuk mengetahui aturan-aturan dasar apa saja yang digunakan pada soal ini.
Carilah banyaknya huruf yang bisa dihemat, apabila semua bilangan Romawi pada berkas teks tersebut ditulis dengan cara yang paling efisien.
Catatan: Anda dapat mengasumsikan semua bilangan Romawi yang ada di berkas teks tersebut tidak ada yang memiliki empat huruf yang sama secara berurutan.
Answer: 5c572eca050594c7bc3c36e7e8ab9550
Soal 90
Setiap sisi pada kubus ditulisi angka yang berbeda (0 sampai 9); hal yang sama dilakukan pada kubus yang kedua. Dengan meletakkan kedua kubus secara bersebelahan pada berbagai posisi yang berbeda, kita dapat membentuk berbagai macam bilangan 2 digit.
Sebagai contoh, bilangan kuadrat 64 dapat dibentuk dengan cara:
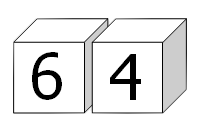
Dengan memilih angka pada kubus secara saksama, kita dapat menampilkan semua bilangan kuadrat kurang dari seratus: 01, 04, 09, 16, 25, 36, 49, 64, and 81.
Sebagai contoh, salah satu caranya adalah dengan menuliskan {0, 5, 6, 7, 8, 9} pada kubus yang pertama dan {1, 2, 3, 4, 8, 9} pada kubus yang lainnya.
Tetapi, untuk soal ini, kita harus memperbolehkan untuk membalik angka 6 atau 9, sehingga susunan {0, 5, 6, 7, 8, 9} dan {1, 2, 3, 4, 6, 7} dapat menghasilkan kesembilan bilangan kuadrat di atas; apabila tidak diperbolehkan, akan mustahil untuk membentuk bilangan 09.
Saat menentukan susunan kubus yang berbeda, kita hanya memperhatikan angka-angka pada setiap kubus, bukan posisinya.
{1, 2, 3, 4, 5, 6} sama dengan {3, 6, 4, 1, 2, 5}
{1, 2, 3, 4, 5, 6} berbeda dengan {1, 2, 3, 4, 5, 9}
Namun karena kita memperbolehkan angka 6 dan 9 untuk dibalik, maka dua himpunan berbeda pada contoh terakhir, keduanya akan dianggap sebagai himpunan {1, 2, 3, 4, 5, 6, 9} saat digunakan untuk membentuk bilangan 2 digit.
Berapa banyak susunan kubus yang berbeda yang diperlukan supaya semua bilangan kuadrat dapat ditampilkan?
Answer: 6a61d423d02a1c56250dc23ae7ff12f3
Soal 91
Titik P (x1, y1) dan Q (x2, y2) memiliki koordinat berupa bilangan bulat, dan apabila digabung dengan titik asal, O(0,0), akan terbentuk ΔOPQ.
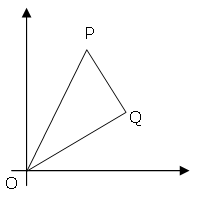
Terdapat persis empat belas segitiga siku-siku, yang dapat dibentuk jika koordinat berada di antara selang tertutup antara 0 dan 2; atau dapat ditulis
0 ≤ x1, y1, x2, y2 ≤ 2.
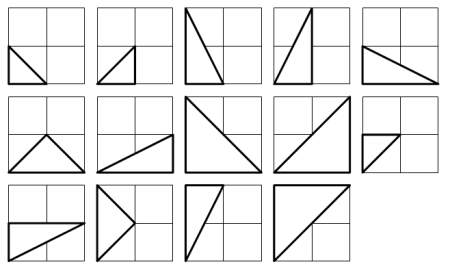
Diberikan 0 ≤ x1, y1, x2, y2 ≤ 50, berapa banyak segitiga siku-siku yang dapat dibentuk?
Answer: e8dc153260a59d4f236cfd7439d5dfd3
Soal 92
Sebuah rantai angka dapat dibuat dengan menjumlahkan terus menerus hasil kuadrat digit-digit dalam suatu bilangan, untuk membentuk bilangan baru, dan berhenti sampai ada bilangan sama yang muncul kembali.
Sebagai contoh,
44 → 32 → 13 → 10 → 1 → 1
85 → 89 → 145 → 42 → 20 → 4 → 16 → 37 → 58 → 89
Karena itu, semua rantai yang terdapat bilangan 1 atau 89 akan terus menerus berputar. Yang istimewa adalah APAPUN angka mulainya, apabila dikerjakan dengan cara di atas, akan selalu tiba di 1 atau 89.
Berapa banyak bilangan awal dalam rantai seperti ini, yang besarnya kurang dari sepuluh juta, yang berakhir pada 89?
Answer: 6cee918c0612bccc2dac03d05e07035f
Soal 93
Dengan menggunakan semua bilangan dari himpunan {1, 2, 3, 4} masing-masing satu kali, dan menggunakan semua operasi aritmatika yang ada (+, −, *, /) serta dengan menggunakan tanda kurung, kita dapat membuat bilangan bulat positif baru.
Sebagai contoh,
8 = (4 * (1 + 3)) / 2
14 = 4 * (3 + 1 / 2)
19 = 4 * (2 + 3) − 1
36 = 3 * 4 * (2 + 1)
Perhatikan bahwa perangkaian digit, seperti 12 + 34, adalah tidak diperbolehkan.
Menggunakan himpunan, {1, 2, 3, 4}, kita dapat mendapatkan tiga puluh satu buah bilangan bulat baru berbeda, dan bilangan 36 adalah yang paling besar, dan semua angka dari 1 sampai 28 masih bisa dibentuk oleh himpunan tersebut, sebelum akhirnya tidak ada lagi bilangan yang bisa dibentuk.
Carilah himpunan empat digit berbeda, a < b < c < d, di mana himpunan tersebut dapat menghasilkan bilangan-bilangan baru berurutan yang paling panjang, dari 1 sampai n. Berikan jawaban anda dalam format tulisan: abcd.
Answer: 26588e932c7ccfa1df309280702fe1b5
Soal 94
Kita dapat dengan mudah membuktikan, bahwa tidak terdapat segitiga sama sisi yang memiliki panjang sisi dan luas berupa bilangan bulat. Namun, terdapat segitiga yang hampir sama sisi 5-5-6 dan memiliki luas 12 satuan.
Kita akan menetapkan, bahwa sebuah segitiga yang hampir sama sisi adalah sebuah segitiga yang dua buah sisinya sama panjang, dan panjang sisi ketiganya boleh berbeda tidak lebih dari satu satuan panjang dengan sisi lainnya.
Carilah jumlah keliling dari semua segitiga yang hampir sama sisi, yang memiliki panjang sisi dan luas berupa bilangan bulat, dan keliling masing-masing segitiganya tidak melebihi satu miliar (1.000.000.000).
Answer: 3218c6bb59f2539ec39ad4bf37c10913
Soal 95
Pembagi wajar dari suatu bilangan adalah kumpulan semua bilangan yang dapat membaginya habis, kecuali bilangan itu sendiri. Sebagai contoh, pembagi wajar dari 28 adalah 1, 2, 4, 7, dan 14. Lalu karena jumlah semua pembagi wajar tersebut juga sama dengan 28, kita dapat menyebut bilangan tersebut adalah bilangan sempurna.
Menariknya, hasil penjumlahan dari semua pembagi wajar 220 adalah 284 dan hasil penjumlahan dari semua pembagi wajar 284 adalah 220, terdapat “rantai” antara kedua bilangan tersebut. Karena adanya rantai tersebut, 220 dan 284 dapat disebut pasangan akrab.
Terdapat contoh bilangan lain yang dapat membentuk rantai lebih panjang. Sebagai contoh, dimulai dari 12496, kita dapat membentuk rantai dengan panjang lima bilangan:
12496 → 14288 → 15472 → 14536 → 14264 (→ 12496 → …)
Karena rantai ini kembali ke angka awalnya, maka rantai ini akan disebut rantai akrab.
Carilah bilangan terkecil, yang dapat membuat rantai akrab terpanjang, yang bilangan-bilangan pada rantainya tidak melebihi satu juta.
Answer: cd2018beeece5fb0a71a96308e567bde
Soal 96
Su Doku (jika diterjemahkan dari bahasa Jepang berarti letak angka) adalah nama yang diberikan untuk sebuah konsep teka-teki yang populer. Asal mulanya tidak diketahui, namun kita harus menghargai jasa Leonhard Euler yang menemukan ide teka-teki hampir serupa, dan lebih menantang, yang disebut kotak-kotak Latin ("Latin Squares"). Tujuan dari teka-teki Su Doku adalah untuk mengganti kotak kosong (atau nol) dalam kotak-kotak berukuran 9 x 9 dan pada setiap baris, kolom, dan kotak ukuran 3 x 3, terdapat semua angka dari 1 sampai 9. Berikut ini adalah contoh dari awal teka-teki, dan solusinya.
|
|
Sebuah teka-teki Su Doku yang baik memiliki solusi yang unik dan dapat diselesaikan oleh logika, walaupun terkadang diperlukan cara "coba-coba" dalam mencari solusi yang ada. Tingkat kesulitan dari teka-teki ini ditentukan oleh kerumitan mencari solusi; contoh di atas dapat dianggap sebagai contoh mudah karena dapat diselesaikan secara langsung, dengan mengamati kotak satu per satu.
Sebuah berkas teks berukuran 6K, [sudoku.txt](/projecteuler/files/sudoku.txt) (klik kanan dan pilih 'Save Link/Target As...'), berisi lima puluh teka-teki Su Doku berbeda, dari berbagai tingkat kesulitan, namun semua teka-teki tersebut memiliki solusi yang berbeda (teka-teki yang pertama sama dengan contoh di atas).
Dengan menyelesaikan kelima puluh teka-teki yang ada, carilah jumlah dari semua 3 angka pertama pada pojok kiri atas; sebagai contoh, pada contoh teka-teki di atas, 3 angka pertama pada pojok kiri atasnya adalah 483.
Answer: 26f6abfa0d7725fef678e371897d5df0
Soal 97
Bilangan prima pertama yang memiliki lebih dari satu juta digit telah berhasil ditemukan pada tahun 1999. Bilangan tersebut merupakan bilangan prima Mersenne, yaitu 26972593−1; bilangan tersebut memiliki persis 2.098.960 digit. Kemudian bilangan prima Mersenne lainnya, dengan bentuk 2p−1, telah ditemukan, dan bilangan tersebut memiliki digit yang lebih banyak.
Namun, pada tahun 2004 ditemukan sebuah bilangan prima bukan Mersenne besar yang memiliki 2.357.207 digit: 28433×27830457+1.
Carilah sepuluh angka terakhir dari bilangan prima ini.
Answer: 68c8c919526039022b923a72d5cc12b1
Soal 98
Dengan menukarkan setiap huruf dalam kata CARE dengan angka 1, 2, 9, dan 6 secara berurutan, kita dapat membentuk sebuah bilangan kuadrat: 1296 = 362. Yang mengesankan adalah, dengan menggunakan aturan penukaran yang sama, kata RACE, juga akan membentuk sebuah bilangan kuadrat: 9216 = 962. Kita akan menyebut kata CARE (dan RACE) sebagai kata kuadrat anagramik. Perlu diketahui bahwa digit pertama nol tidak diizinkan, dan juga tidak diperbolehkan untuk memberikan digit yang sama pada huruf yang berbeda.
Menggunakan [words.txt](/projecteuler/files/words.txt) (klik kanan dan pilih 'Save Link/Target As...'), sebuah berkas teks berukuran 16K yang berisi hampir dua ribu kata dalam bahasa Inggris, carilah semua pasangan kata kuadrat anagramik (kata yang palindrom, TIDAK dianggap sebagai anagram dari dirinya sendiri).
Berapakah bilangan kuadrat terbesar yang ada?
CATATAN: Semua anagram yang mungkin terbentuk pasti sudah ada dalam berkas teks tersebut.
Answer: 36b3b5f54143786b7ab2ebb6bcd06e75
Soal 99
Membandingkan dua buah bilangan dalam bentuk perpangkatan seperti 211 dan 37 tidaklah sulit, karena hampir semua kalkulator dapat membuktikan 211 = 2048 < 37 = 2187.
Tetapi, membuktikan 632382518061 > 519432525806 akan lebih sulit, karena kedua bilangan memiliki lebih dari tiga juta digit.
Menggunakan [base_exp.txt](/projecteuler/files/base_exp.txt) (klik kanan dan pilih 'Save Link/Target As...'), sebuah berkas teks berukuran 22K yang berisi seribu baris pasangan bilangan dengan pangkatnya, carilah baris ke berapakah yang memiliki hasil paling besar.
CATATAN: dua baris pertama pada berkas teks tersebut adalah sama seperti bilangan contoh di atas.
Answer: 1ecfb463472ec9115b10c292ef8bc986
Soal 100
Sebuah kotak berisi dua puluh satu cakram berwarna, yang terdiri dari lima belas cakram biru, dan enam cakram merah, dan dua cakram diambil secara acak secara satu persatu. Dapat terlihat peluang untuk mengambil dua cakram biru, P(BB) = (15/21)×(14/20) = 1/2.
Susunan lainnya, dengan peluang untuk mendapatkan cakram biru juga 50% , adalah sebuah kotak yang berisi delapan puluh lima cakram biru, dan tiga puluh lima cakram merah.
Carilah susunan lainnya yang berisi lebih dari 1012 = 1,000,000,000,000 buah cakram, dan tentukan berapakan jumlah cakram biru dalam kotak tersebut, sehingga peluang mengambil dua cakram biru juga 50%.
Answer: 21156e3acc4ca35b7a318c541a0648d5
Soal 101
Jika kita diberikan k buah suku pertama dari suatu barisan bilangan, tidak mungkin kita dapat menentukan nilai dari suku selanjutnya, karena terdapat tak terhingga kemungkinan rumus suku banyak yang bisa sesuai dengan barisan tersebut.
Misalnya kita lihat barisan bilangan kubik. Barisan ini dibentuk dengan fungsi pembangkit
un = n3: 1, 8, 27, 64, 125, 216, ...
Misalkan kita hanya diberikan dua suku pertama dari barisan ini. Dengan menerapkan prinsip "makin sederhana makin baik" kita mungkin akan beranggapan bahwa barisan tersebut adalah barisan linear, dan memprediksi suku selanjutnya adalah 15 (karena memiliki beda yang sama, yaitu 7). Bahkan jika kita diberikan tiga suku pertama, dengan prinsip "makin sederhana makin baik", kita mungkin bisa beranggapan bahwa hubungan barisan tersebut adalah hubungan kuadrat.
OP(k, n) adalah fungsi yang akan memiliki k buah suku pertama yang benar saat dicocokkan dengan barisan, jika nilai n disubtitusikan. OP(k, n) akan memiliki suku yang sesuai untuk n ≤ k, dan kemungkinan suku yang tidak sesuai pertama akan ditemukan saat OP(k, k+1); yang dalam soal ini akan disebut sebagai bad OP (BOP), yang berarti suku banyak optimum yang keliru.
Sebagai contoh, jika kita hanya diberikan suku pertama dari barisan, kita mungkin akan menganggap barisan tersebut memiliki rumus konstan; sehingga, untuk n ≥ 2, OP(1, n) = u1.
Sehingga kita dapat menghitung OP untuk barisan bilangan kubik berikut:
| OP(1, n) = 1 | 1, 1, 1, 1, ... |
| OP(2, n) = 7n−6 | 1, 8, 15, ... |
| OP(3, n) = 6n2−11n+6 | 1, 8, 27, 58, ... |
| OP(4, n) = n3 | 1, 8, 27, 64, 125, ... |
Dapat terlihat bahwa tidak ada kesalahan lagi (tidak ada BOP) saat k ≥ 4.
Dengan menjumlahkan suku-suku pertama yang salah, saat dibuat rumus OP (ditandai dengan warna merah pada bagian di atas), kita akan mendapatkan 1 + 15 + 58 = 74.
Misalkan terdapat sebuah fungsi pembangkit suku banyak derajat sepuluh:
un = 1 − n + n2 − n3 + n4 − n5 + n6 − n7 + n8 − n9 + n10
Carilah jumlah suku-suku pertama yang salah, saat dibuat rumus OP.
Answer: d382b0cc25e82446da83d3a792e1cd27
Soal 102
Tiga titik berbeda ditaruh secara acak pada bidang kartesius, di mana tiap titik memiliki koordinat (x,y) memenuhi -1000 ≤ x, y ≤ 1000, sedemikian rupa sehingga ketiganya membentuk segitiga.
Misalkan terdapat dua segitiga:
A(-340,495), B(-153,-910), C(835,-947)
X(-175,41), Y(-421,-714), Z(574,-645)
Dapat dibuktikan bahwa segitiga ABC mengurung titik asal O(0,0), dan segitiga XYZ tidak.
Dengan menggunakan triangles.txt (klik kanan dan pilih ‘Save Link/Target As…’), sebuah berkas teks berukuran 27K yang berisi koordinat dari seribu buah segitiga acak, carilah banyaknya segitiga yang mengurung titik asal O(0,0).
CATATAN: dua contoh pertama pada berkas teks sama dengan contoh di atas.
Answer: 74db120f0a8e5646ef5a30154e9f6deb
Soal 103
Misalkan S(A) adalah melambangkan penjumlahan dari elemen-elemen dalam himpunan A dengan banyak anggota n. Himpunan A akan disebut memiliki penjumlahan istimewa apabila dua himpunan bagiannya yang tidak kosong dan saling lepas, B dan C, memenuhi sifat-sifat berikut:
- S(B) ≠ S(C); sehingga, hasil penjumlahan dari semua himpunan bagian tidak boleh sama.
- Jika B memiliki anggota yang lebih banyak dari C, maka S(B) > S(C).
Jika S(A) bisa diminimumkan untuk suatu nilai n, maka kita akan menyebut bahwa himpunan tersebut memiliki penjumlahan istimewa optimal. Lima penjumlahan istimewa optimal pertama adalah sebagai berikut.
n = 1: {1}
n = 2: {1, 2}
n = 3: {2, 3, 4}
n = 4: {3, 5, 6, 7}
n = 5: {6, 9, 11, 12, 13}
Dapat terlihat bahwa untuk suatu himpunan optimal, A = {a1, a2, ... , an}, himpunan optimal selanjutnya adalah B = {b, a1+b, a2+b, ... ,an+b}, di mana b adalah anggota "tengah" dari baris sebelumnya.
Dengan menerapkan "aturan" ini, kita bisa menduga bahwa himpunan optimum selanjutnya untuk n = 6 akan menjadi A = {11, 17, 20, 22, 23, 24}, dengan S(A) = 117. Tetapi, ternyata himpunan ini bukanlah yang paling optimal, karena kita hanya menggunakan algoritma yang membuat himpunan mendekati optimal. Himpunan optimal untuk n = 6 adalah A = {11, 18, 19, 20, 22, 25}, dengan S(A) = 115 dan untai himpunan yang terkait adalah: 111819202225.
Misalnya A adalah himpunan istimewa optimal untuk n = 7, maka carilah untai himpunannya.
CATATAN: Soal ini berhubungan dengan Soal 105 dan Soal 106.
Answer: af8c238336c2a79bb81a24b3fef3330d
Soal 104
Barisan Fibonacci bisa didapat dari hubungan berikut:
Fn = Fn−1 + Fn−2, di mana F1 = 1 dan F2 = 1.
Ditemukan bahwa F541, yang memiliki 113 digit, adalah bilangan Fibonacci pertama yang sembilan digit terakhirnya adalah pandigital 1-9 (mengandung semua angka dari 1 sampai 9, namun tidak harus berurutan). Dan F2749, yang memiliki 575 digit, adalah bilangan Fibonacci pertama yang sembilan digit pertamanya adalah pandigital 1-9.
Diketahui Fk adalah bilangan Fibonacci pertama yang sembilan digit pertama DAN sembilan digit terakhirnya adalah pandigital 1-9, carilah nilai k.
Answer: c8771ddd4df191098d70a8e94dd1cde7
Soal 105
Misalkan S(A) melambangkan hasil penjumlahan dari elemen-elemen dalam himpunan A dengan banyak anggota n. Himpunan A akan disebut memiliki penjumlahan istimewa apabila dua himpunan bagiannya yang tidak kosong dan saling lepas, B dan C, memenuhi sifat-sifat berikut:
- S(B) ≠ S(C); sehingga, hasil penjumlahan dari semua himpunan bagian tidak boleh sama.
- Jika B memiliki anggota yang lebih banyak dari C, maka S(B) > S(C).
Sebagai contoh, {81, 88, 75, 42, 87, 84, 86, 65} bukanlah himpunan yang memiliki penjumlahan istimewa, sebab dapat ditemukan 65 + 87 + 88 = 75 + 81 + 84, contoh lain {157, 150, 164, 119, 79, 159, 161, 139, 158} memenuhi kedua sifat di atas untuk semua kombinasi himpunan bagian yang mungkin, dan S(A) = 1286.
Menggunakan [sets.txt](/projecteuler/files/sets.txt) (klik kanan dan pilih "Save Link/Target As..."), sebuah berkas teks berukuran 4K yang berisi seratus himpunan yang memiliki tujuh sampai dua belas anggota (dua contoh di atas adalah dua himpunan pertama dalam berkas tersebut), carilah semua himpunan yang memiliki penjumlahan istimewa, A1, A2, ..., Ak, dan carilah nilai dari S(A1) + S(A2) + ... + S(Ak).
CATATAN: Soal ini berhubungan dengan Soal 103 dan Soal 106.
Answer: c87d30e494eff438fe37b4c810167da0
Soal 106
Misalkan S(A) adalah hasil penjumlahan dari elemen-elemen dalam himpunan A dengan banyak anggota n. Himpunan A akan disebut memiliki penjumlahan istimewa apabila dua himpunan bagiannya yang tidak kosong dan saling lepas, B dan C, memenuhi sifat-sifat berikut:
- S(B) ≠ S(C); sehingga, hasil penjumlahan dari semua himpunan bagian tidak boleh sama.
- Jika B memiliki anggota yang lebih banyak dari C, maka S(B) > S(C).
Untuk soal ini, kita akan asumsikan bahwa himpunan dengan n anggota berisi bilangan yang terus membesar, dan pasti memenuhi sifat kedua.
Mengejutkan bahwa dari 25 pasangan himpunan bagian yang ada, yang bisa didapat dari himpunan dengan n = 4, hanya 1 dari pasangan tersebut yang perlu diuji untuk sifat pertama. Sementara itu, saat n = 7, hanya 70 dari 966 himpunan bagian yang ada yang perlu diuji.
Untuk n = 12, berapa banyak pasangan yang perlu diuji dengan sifat pertama, dari 261625 pasangan himpunan bagian yang ada?
NOTE: Soal ini berhubungan dengan Soal 103 dan Soal 105.
Answer: c8fd9e36fdeb06bcc93a0732c667b6d8
Soal 107
Jaringan takberarah berikut ini memiliki dari tujuh verteks (titik) dan dua belas rusuk with a total bobot 243.
Jaringan di atas dapat dilambangkan pula sebagai matriks berikut ini.
| A | B | C | D | E | F | G | |
| A | - | 16 | 12 | 21 | - | - | - |
| B | 16 | - | - | 17 | 20 | - | - |
| C | 12 | - | - | 28 | - | 31 | - |
| D | 21 | 17 | 28 | - | 18 | 19 | 23 |
| E | - | 20 | - | 18 | - | - | 11 |
| F | - | - | 31 | 19 | - | - | 27 |
| G | - | - | - | 23 | 11 | 27 | - |
Kita dapat menyederhanakan jaringan tersebut dengan membuang beberapa rusuk, dan semua verteks masih tetap terhubung. Jaringan yang paling sederhana ditunjukkan pada gambar di bawah. Jaringan ini memiliki bobot 93, dan dapat menghemat 243 − 93 = 150 bobot, dari jaringan mula-mula.
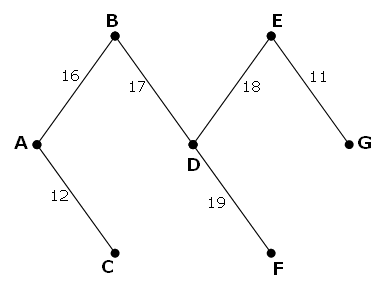
Menggunakan [network.txt](/projecteuler/files/network.txt) (klik kanan dan pilih 'Save Link/Target As...'), sebuah berkas berukuran 6K berisi sebuah jaringan dengan empat puluh verteks, dan diberikan dalam bentuk matriks, carilah jumlah penghematan maksimum yang dapat dilakukan, dengan membuang beberapa ruas namun dengan memastikan bahwa semua verteks tetap terhubung.
Answer: b0db1202ec966e7855ca23626eb285b8
Soal 108
Dalam persamaan berikut x, y, dan n adalah bilangan bulat positif.
1 1 1
─ + ─ = ─
x y n
Untuk n = 4 terdapat persis empat solusi berbeda:
1 1 1
─ + ─ = ─
5 20 4
1 1 1
─ + ─ = ─
6 12 4
1 1 1
─ + ─ = ─
8 8 4
Berapakah nilai terkecil n sehingga terdapat solusi berbeda yang banyaknya melebihi seribu buah?
CATATAN: Soal ini adalah versi lebih mudah dari Soal 110; dan sangat disarankan Anda menyelesaikan soal ini terlebih dahulu.
Answer: 765ba18edd2844db2db95fba25d2f3e7
Soal 109
Dalam permainan darts, seorang pemain akan melempar tiga batang dart (panah kecil) ke papan target yang dibagi menjadi dua puluh bagian yan g sama besar, diberi angka dari satu sampai dua puluh.
Nilai dari sebatang dart ditentukan dari angka yang dimiliki oleh daerah tempat dart tersebut mendarat. Jika dart mendarat di luar lingkaran merah/hijau, maka pemain akan mendapat nilai nol. Daerah berwarna hitam dan krim dalam lingkaran akan mengalikan nilai dengan satu. Tetapi, garis merah/hijau pada bagian luar dan bagian tengah lingkaran akan melipatgandakan nilai, masing-masing menjadi dua kali (double) dan tiga kali (treble).
Pada tengah-tengah papan, terdapat dua lingkaran sepusat yang disebut bull region, atau bulls-eye. Bagian luar bull bernilai 25 poin, dan bagian dalam bull adalah double bull dan bernilai dua kali lipatnya, yaitu 50 poin.
Terdapat berbagai variasi dari aturan yang ada, namun aturan yang paling sering digunakan adalah para pemain akan mulai dengan skor 301 atau 501, dan pemain pertama yang bisa mengurangi skornya sampai nol adalah pemenangnya. Tetapi, setiap pemain harus memperhatikan sistem "doubles out", di mana setiap pemain harus mendaratkan dart terakhir mereka di mana saja yang memiliki nilai double(termasuk double bulls-eye berwarna merah di tengah papan) untuk menang; setiap tiga dart yang membuat nilai total pemain menjadi satu atau kurang dari satu, akan mengakibatkan skor ketiga dart tersebut diabaikan ("bust").
Saat seorang pemain dapat menyelesaikan permainannya, hal itu disebut "checkout" dan skor checkout tertinggi yang bisa didapat adalah 170: T20 T20 D25 (dua treble 20s dan double bull).
Terdapat sebelas cara berbeda untuk melakukan checkout pada nilai 6:
D3 |
||
| D1 | D2 | |
| S2 | D2 | |
| D2 | D1 | |
| S4 | D1 | |
| S1 | S1 | D2 |
| S1 | T1 | D1 |
| S1 | S3 | D1 |
| D1 | D1 | D1 |
| D1 | S2 | D1 |
| S2 | S2 | D1 |
Perhatikan bahwa D1 D2 dianggap berbeda dengan D2 D1, karena mereka selesai di double yang berbeda. Tetapi, kombinasi S1 T1 D1 dianggap sama dengan T1 S1 D1.
Sebagai tambahan, kita tidak akan mengikut sertakan dart yang meleset dalam kombinasi; sebagai contoh, D3 adalah sama dengan 0 D3 dan 0 0 D3.
Luar biasanya, ternyata terdapat 42336 cara berbeda untuk melakukan checkout.
Berapa banyak cara pemain dapat melakukan checkout pada nilai kurang dari 100?
Answer: e6aebd5be1ba81557dbcc5f6f57bbe5c
Soal 110
Dalam persamaan berikut x, y, dan n adalah bilangan bulat positif.
1 1 1
─ + ─ = ─
x y n
Dapat dibuktikan bahwa saat n = 1260 terdapat 113 buah solusi berbeda, dan ini adalah merupakan nilai n terkecil yang akan menghasilkan solusi berbeda sebanyak lebih dari seratus buah.
Berapakah nilai terkecil n sehingga terdapat solusi berbeda yang banyaknya melebihi empat juta?
CATATAN: Soal ini adalah versi yang lebih sulit dari Soal 108 dan tidak memungkinkan untuk diselesaikan dengan cara mencoba satu persatu, perlu cara yang cerdas untuk menyelesaikan soal ini.
Answer: 591a7a92f10322866e6a02f3b2386a1c
Soal 111
Apabila suatu bilangan prima 4-digit memiliki digit yang berulang, jelas bahwa tidak mungkin keempat digit tersebut semuanya sama: 1111 habis dibagi 11, 2222 habis dibagi 22, dan seterusnya. Namun terdapat sembilan buah bilangan prima 4-digit yang memiliki tiga buah digit satu:
1117, 1151, 1171, 1181, 1511, 1811, 2111, 4111, 8111
Kita akan menyatakan bahwa M(n, d) melambangkan banyak maksimal dari digit yang berulang untuk bilangan prima digit-n, di mana d adalah digit yang akan berulang, N(n, d) melambangkan banyaknya bilangan prima tersebut, dan S(n, d) melambangkan jumlah dari bilangan-bilangan prima tersebut.
Sehingga M(4, 1) = 3 adalah jumlah maksimal digit yang boleh berulang, untuk bilangan prima 4 digit, di mana digit berulangnya adalah satu, terdapat N(4, 1) = 9 buah bilangan prima yang memenuhi sifat sebelumnya, dan jumlah dari bilangan-bilangan prima tersebut adalah S(4, 1) = 22275. Lalu untuk d = 0, digit tersebut hanya memungkinkan diulang M(4, 0) = 2 kali, namun terdapat N(4, 0) = 13 buah bilangan prima pada kasus tersebut.
Dengan cara yang sama, kita akan mendapatkan hasil berikut untuk bilangan prima 4-digit.
| Digit, d | M(4, d) | N(4, d) | S(4, d) |
| 0 | 2 | 13 | 67061 |
| 1 | 3 | 9 | 22275 |
| 2 | 3 | 1 | 2221 |
| 3 | 3 | 12 | 46214 |
| 4 | 3 | 2 | 8888 |
| 5 | 3 | 1 | 5557 |
| 6 | 3 | 1 | 6661 |
| 7 | 3 | 9 | 57863 |
| 8 | 3 | 1 | 8887 |
| 9 | 3 | 7 | 48073 |
Untuk d = 0 sampai 9, jumlah semua bilangan primanya S(4, d) adalah 273700.
Carilah jumlah dari semua S(10, d).
Answer: cdf4d134a3b0caa10a69e2771ac4fd36
Soal 112
Dimulai dari kiri ke kanan, apabila digit dalam suatu bilangan lebih besar daripada digit di sebelah kirinya, maka bilangan itu akan disebut sebagai bilangan bertambah; sebagai contoh, 134468.
Dengan cara yang sama, apabila digit dalam suatu bilangan tidak lebih besar dari digit di sebelah kanannya, maka bilangan itu akan disebut bilangan berkurang; sebagai contoh, 66420.
Kita akan menyebut bilangan positif yang bukan merupakan bilangan bertambah atau juga bilangan berkurang sebagai bilangan “bouncy”; sebagai contoh, 155349.
Jelas bahwa tidak mungkin ada bilangan bouncy yang lebih kecil dari seratus. Namun hampir separuh dari bilangan di bawah seribu adalah bilangan bouncy (525 buah). Pada kenyataannya, pada bilangan 538 untuk pertama kalinya persentase bilangan “bouncy” di bawahnya menjadi 50%.
Cukup mengejutkan bahwa bilangan bouncy menjadi semakin sering ditemui saat kita sampai ke bilangan 21780. Pada titik tersebut, persentase banyaknya bilangan bouncy di bawahnya adalah 90%.
Carilah pada bilangan berapa, proporsi bilangan bouncy di bawahnya akan menjadi 99%?
Answer: e08c982713a1c2bd3637dd489199722e
Soal 113
Dimulai dari kiri ke kanan, apabila digit dalam suatu bilangan lebih besar daripada digit di sebelah kirinya, maka bilangan itu akan disebut sebagai bilangan bertambah; sebagai contoh, 134468.
Dengan cara yang sama, apabila digit dalam suatu bilangan tidak lebih besar dari digit di sebelah kanannya, maka bilangan itu akan disebut bilangan berkurang; sebagai contoh, 66420.
Kita akan menyebut bilangan positif yang bukan merupakan bilangan bertambah atau juga bilangan berkurang sebagai bilangan "bouncy" sebagai contoh, 155349.
Saat nilai n semakin meningkat, banyaknya bilangan bouncy yang lebih kecil dari n juga akan semakin meningkat, sebagai contoh, hanya ada 12951 buah bilangan yang lebih kecil dari satu juta yang bukan merupakan bilangan bouncy, dan hanya terdapat 277032 buah bilangan yang lebih kecil dari 1010 yang bukan merupakan bilangan bouncy.
Berapakah banyaknya bilangan yang lebih kecil dari 10100 yang bukan merupakan bilangan bouncy?
Answer: a9e504ee704c87f9bddad6d3ffe39532
Soal 114
Suatu barisan kotak dengan panjang tujuh satuan, yang memiliki kotak merah yang panjang minimalnya tiga satuan. Jika terdapat dua bagian ko tak berwarna merah (dimana kedua kotak merah boleh memiliki panjang berbeda), kedua bagian tersebut harus dipisahkan oleh setidaknya satu kotak hitam. Terdapat persis tujuh belas kombinasi dari masalah ini.
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||
Berapa banyak cara mengisi kotak merah pada sebuah barisan kotak dengan panjang lima puluh satuan dengan aturan di atas?
CATATAN: Belum terlihat pada contoh di atas, bahwa Anda diperbolehkan untuk menggunakan dua bagian kotak merah berbeda ukuran. Sebagai contoh, pada blok kotak berukuran delapan satuan panjang, anda dapat menggunakan susunan merah (3), hitam (1), dan merah (4).
Answer: de48ca72bf252a8be7e0aad762eadcf8
Soal 115
CATATAN: Ini adalah versi yang lebih menantang dari Soal 114.
Sebuah barisan kotak berukuran n satuan panjang berisi kotak merah dengan panjang minimal m satuan, dan barisan tersebut boleh memiliki dua bagian kotak merah yang wajib dipisahkan oleh setidaknya satu kotak hitam (kedua bagian kotak merah boleh memiliki panjang berbeda).
Misalkan terdapat fungsi F(m, n), yang merupakan banyaknya cara barisan kotak berukuran n tersebut dapat diisi.
Sebagai contoh, F(3, 29) = 673135 dan F(3, 30) = 1089155.
Dari fungsi di atas terlihat, bahwa saat m = 3, nilai n = 30 adalah nilai n terkecil yang akan membuat banyaknya cara menyusun kotak merah melebihi satu juta cara.
Denagn cara yang sama, untuk m = 10, dapat dibuktikan bahwa F(10, 56) = 880711 dan F(10, 57) = 1148904, sehingga n = 57 adalah nilai n terkecil yang akan membuat banyaknya cara menyusun kotak merah melebihi satu juta cara.
Untuk m = 50, carilah nilai n terkecil, sehingga ada lebih dari satu juta cara untuk menyusun kotak merah.
Answer: 006f52e9102a8d3be2fe5614f42ba989
Soal 116
Kita akan mengganti tegel pada barisan berisi lima tegel hitam dengan tegel lain yang berbeda warna, yaitu merah (panjang dua satuan), hijau (panjang tiga satuan), atau biru (panjang empat satuan).
Jika tegel merah dipilih untuk mengisi barisan di atas, maka terdapat persis tujuh cara yang ada.
┌─╥╥╥┐ ┌╥─╥╥┐ ┌╥╥─╥┐ ┌╥╥╥─┐
└─╨╨╨┘ └╨─╨╨┘ └╨╨─╨┘ └╨╨╨─┘
┌─╥─╥┐ ┌─╥╥─┐ ┌╥─╥─┐
└─╨─╨┘ └─╨╨─┘ └╨─╨─┘
Jika kotak hijau yang dipilih, terdapat tiga cara untuk mengisi kotak hitam.
┌──╥╥┐ ┌╥──╥┐ ┌╥╥──┐
└──╨╨┘ └╨──╨┘ └╨╨──┘
Dan jika kotak biru yang dipilih, terdapat dua cara untuk mengisi kotak hitam.
┌╥───┐ ┌───╥┐
└╨───┘ └───╨┘
Jika warna-warna yang ada tidak boleh dicampur, maka akan terdapat 7 + 3 + 2 = 12 cara untuk mengganti tegel hitam yang memiliki panjang lima satuan.
Berapakah banyaknya cara tegel hitam dengan panjang lima puluh satuan dapat diganti dengan cara seperti di atas, dan kita hanya diperbolehkan menggantinya dengan satu warna?
CATATAN: Soal ini berhubungan dengan Soal 117.
Answer: c21ca0ec54e6d1646a953a480f68feb4
Soal 117
Dengan menggunakan kombinasi dari: kotak merah dengan panjang dua satuan, kotak hijau dengan panjang tiga satuan, dan kotak biru dengan panjang empat satuan, kita dapat mengisi kotak hitam dengan panjang lima satuan dengan berbagai cara.
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
Berapa banyak cara kotak hitam dengan panjang lima puluh satuan dapat di isi?
CATATAN: Soal ini berhubungan dengan Soal 116.
Answer: 542612809b3dd08cf518b85450fce8d6
Soal 118
Dengan menggunakan akanga 1 sampai 9, dan menyatukan mereka secara acak untuk membentuk suatu bilangan bulat, berbagai himpunan dapat dibentuk. Menariknya, himpunan {2,5,47,89,631}, memiliki anggota-anggota yang semuanya adalah bilangan prima.
Berapakah banyaknya himpunan berbeda, yang anggota-anggotanya dibentuk menggunakan angka 1 sampai 9 persis satu kali, yang semua anggotanya adalah bilangan prima?
Answer: 080cc5a4ec71a747e260e274bdb13b64
Soal 119
Bilangan 512 adalah bilangna yang menarik, karena bilangan ini dapat dibentuk dengan cara menjumlahkan angka-angkanya, lalu memangkatkan hasil penjumlahan tersebut dengan angka tertentu: 5 + 1 + 2 = 8, dan 83 = 512. Contoh bilangan lain yang memiliki sifat seperti ini adalah 614656 = 284.
Kita akan menetapkan an sebagai suku ke n dari barisan bilangan seperti di atas, dan bilangan di atas harus memiliki setidaknya dua angka agar dapat dilakukan penjumlahan.
Diberikah a2 = 512 dan a10 = 614656.
Carilah a30.
Answer: 72fddfa6c52a120892ade628f3819da4
Soal 120
Misalkan r adalah sisa bagi saat (a−1)n + (a+1)n dibagi oleh a2.
Sebagai contoh, jika a = 7 dan n = 3, maka r = 42: 63 + 83 = 728 ≡ 42 mod 49. Dan karena ada bermacam nilai n, maka bermacam juga nilai r yang akan dihasilkan, tetapi untuk a = 7 kita dapat menemukan bahwa rmax = 42.
Untuk 3 ≤ a ≤ 1000, carilah ∑ rmax.
Answer: 0dd05ec40fe11279c2203b72e92a450a
Soal 121
Terdapat sebuah kantong berisi satu disk merah dan satu disk biru. Dalam suatu permainan, seorang pemain akan mengambil sebuah disk secara acak, dan warna disk yang diambil tersebut akan dicatat. Setelah satu putaran, disk akan dikembalikan ke kantong, kemudian ditambahkan satu buah disk merah, dan kembali diambil satu disk secara acak.
Pemain diharuskan membayar £1 untuk bermain, dan ia akan menang apabila ia dapat mengambil disk biru lebih banyak dibanding disk merah saat akhir permainan.
Jika permainan akan berakhir setelah empat putaran, peluang seorang pemain menang adalah 11/120, sehingga jumlah hadiah terbesar harus disediakan oleh bank dalam permainan ini adalah £10 sebelum pemain tersebut akan mengalami kekalahan. Perlu diingat bahwa segala bentuk pembayaran hadiah akan berupa bilangan bulat, dan pada pembayaran akan disertakan juga £1 yang digunakan pertama kali untuk ikut bermain, sehingga pada contoh ini, pemain sesungguhnya hanya memenangkan £9.
Carilah jumlah hadiah terbesar yang harus disediakan oleh bank, pada permainan serupa, namun dengan lima belas putaran.
Answer: 51de85ddd068f0bc787691d356176df9
Soal 122
Cara paling dasar untuk menghitung n15 membutuhkan empat belas kali perkalian:
n × n × ... × n = n15
Tapi dengan menggunakan metode "binary" kita dapat menghitung hal yang sama dengan enam kali perkalian:
n × n = n2
n2 × n2 = n4
n4 × n4 = n8
n8 × n4 = n12
n12 × n2 = n14
n14 × n = n15
Bahkan, memungkinkan untuk menghitung hal yang sama hanya dengan lima kali perkalian:
n × n = n2
n2 × n = n3
n3 × n3 = n6
n6 × n6 = n12
n12 × n3 = n15
Kita akan menyatakan m(k) adalah jumlah perkalian minimal yang dapat digunakan untuk menghitung nk; sebagai contoh m(15) = 5.
Untuk 1 ≤ k ≤ 200, carilah ∑ m(k).
Answer: b710915795b9e9c02cf10d6d2bdb688c
Soal 123
Misalkan pn adalah bilangan prima ke-n: 2, 3, 5, 7, 11, ..., dan misalkan r adalah sisa pembagian dari (pn−1)n + (pn+1)n dibagi oleh pn2.
Sebagai contoh, saat n = 3, p3 = 5, dan 43 + 63 = 280 ≡ 5 mod 25.
Nilai n terkecil yang akan menghasilkan sisa bagi melebihi 109 adalah 7037.
Carilah nilai n terkecil yang akan menghasilkan sisa bagi melebihi 1010.
Answer: 71497f728b86b55d965edbf1849cca8d
Soal 124
Radikal dari n, rad(n), adalah hasil kali dari faktor prima berbeda yang dimiliki oleh n. Sebagai contoh, 504 = 23 × 32 × 7, sehingga rad(504) = 2 × 3 × 7 = 42.
Jika kita menghitung rad(n) untuk 1 ≤ n ≤ 10, lalu mengurutkan bedasarkan rad(n), dan mengurutkan bedasarkan n jika hasil radikalnya sama, maka kita akan mendapatkan:
Unsorted |
Sorted |
||||
n |
rad(n) |
n |
rad(n) |
k |
|
1 | 1 |
1 | 1 | 1 |
|
2 | 2 |
2 | 2 | 2 |
|
3 | 3 |
4 | 2 | 3 |
|
4 | 2 |
8 | 2 | 4 |
|
5 | 5 |
3 | 3 | 5 |
|
6 | 6 |
9 | 3 | 6 |
|
7 | 7 |
5 | 5 | 7 |
|
8 | 2 |
6 | 6 | 8 |
|
9 | 3 |
7 | 7 | 9 |
|
10 | 10 |
10 | 10 | 10 |
|
Misalkan E(k) adalah elemen ke-k pada kolom n yang telah terurut sesuai aturan di atas; sebagai contoh, E(4) = 8 dan E(6) = 9.
Jika rad(n) dihitung dari 1 ≤ n ≤ 100000, sesuai dengan cara di atas, carilah E(10000).
Answer: f228d2e6f9099153388e9470180c8302
Soal 125
Bilangan palindrom 595 memiliki hal yang menarik, karena bilangan ini dapat ditulis sebagai hasil penjumlahan bilangan kuadrat berurutan: 62 + 72 + 82 + 92 + 102 + 112 + 122.
Terdapat persis sebelas bilangan palindrom di bawah seratus yang juga dapat ditulis sebagai hasil penjumlahan bilangan kuadrat berurutan, dan jumlah dari semua bilangan palindrom tersebut adalah 4164. Perlu diingat bahwa 1 = 02 + 12 tidak diikutsertakan dalam perhitungan ini, karena yang diikut sertakan hanya bilangan yang dapat dibuat dari penjumlahan bilangan kuadrat positif saja.
Carilah jumlah semua bilangan palindrom kurang dari 108, yang dapat ditulis sebagai hasil penjumlahan bilangan kuadrat berurutan.
Answer: 1b5635e8ab723e01570ca783129493dd
Soal 126
Jumlah kubus paling sedikit yang diperlukan untuk menutupi permukaan balok dengan ukuran 3 x 2 x 1 adalah dua puluh dua buah.
Jika kita akan menambahkan lapisan kedua, maka kita akan memerulukan empat puluh enam kubus, untuk menutupi semua permukaan, dan lapisan ketiga akan memerlukan tujuh puluh delapan kubus, lalu lapisan ke empat akan memerlukan seratus dan delapan belas kubus untuk menutupi semua permukaan.
Dan, lapisan pertama untuk menutupi balok dengan ukuran 5 x 1 x 1 juga memerlukan dua puluh dua kubus; sedangkan untuk balok berukuran 5 x 3 x 1, 7 x 2 x 1, dan 11 x 1 x 1 semua memerlukan empat puluh enam buah kubus.
Kita akan menyatakan C(n) untuk melambangkan banyaknya balok yang dapat ditutupi dengan n buah kubus pada salah satu lapisannya. Sehingga C(22) = 2, C(46) = 4, C(78) = 5, dan C(118) = 8.
Dapat ditemukan bahwa 154 adalah nilai n terkecil dimana C(n) = 10.
Carilah nilai n terkecil yang akan menghasilkan C(n) = 1000.
Answer: 387d6ae83cbc6fa0b9192b56bf095c49
Soal 127
Nilai radikal dari n, rad(n), adalah hasil perkalian faktor prima berbeda dari n. Sebagai contoh, 504 = 23 × 32 × 7, sehingga rad(504) = 2 × 3 × 7 = 42.
Kita akan mendefinisikan tiga bilangan bulat positif (a, b, c) sebagai abc-hit jika:
- FPB(a, b) = FPB(a, c) = FPB(b, c) = 1
- a < b
- a + b = c
- rad(abc) < c
Sebagai contoh, (5, 27, 32) adalah sebuah abc-hit, karena:
- GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1
- 5 < 27
- 5 + 27 = 32
- rad(4320) = 30 < 32
Dapat terlihat bahwa abc-hits akan cukup jarang untuk ditemui, hanya terdapat tiga puluh satu buah abc-hits untuk c < 1000, dengan cumlah ∑c = 12523.
Carilah ∑c untuk c < 120000.
Answer: c6b1ae935b33c90a2c320b5f6ef3e4ba
Soal 128
Sebuah ubin segienam dengan angka 1 dikelilingi oleh enam buah ubin segienam lainnya, dimulai dari arah "pukul 12" dan ubin di beri nomor 2 sampai 7 secara berlawanan arah jarum jam.
Lapisan baru ditambahkan dengan cara yang sama, dengan lapisan selanjutnya diberi nomor dari 8 sampai 19, 20 sampai 37, 38 sampai 61, dan seterusnya. Diagram berikut ini menunjukkan tiga lapisan pertama.
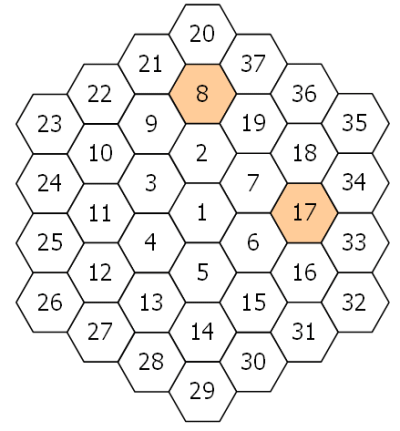
Dengan mencari selisih antara ubin n dengan ke enam buah ubin di sebelahnya, kita akan mendefinisikan PD(n) sebagai banyaknya selisih ubin-ubin tersebut yang merupakan bilangan prima.
Sebagai contoh, jika dihitung searah jarum jam, pada ubin 8, maka didapat selisih 12, 29, 11, 6, 1, dan 13. Sehingga PD(8) = 3.
Dengan cara yang sama, selisih di sekitar ubin 17 adalah 1, 17, 16, 1, 11, dan 10, sehingga PD(17) = 2.
Dapat ditunjukkan bahwa nilai PD(n) terbesar adalah 3.
Jika semua ubin yang memiliki nilai PD(n) = 3 didaftarkan secara berurutan dari kecil ke besar, dan dibentuk suatu barisan bilangan, maka ubin pada urutan ke-10 adalah 271.
Carilah suku ubin ke-2000 pada barisan ini.
Answer: 93a1925da4792b4fa5d2dbb6ebb7c4a2
Soal 129
Sebuah bilangan yang hanya berisi angka satu disebut repunit. Kita akan mendefinisikan R(k) sebagai repunit dengan panjang k; sebagai contoh, R(6) = 111111.
Diberikan bahwa n adalah bilangan bulat positif, dan FPB(n, 10) = 1, dapat ditunjukkan bahwa selalu ada nilai k, dimana R(k) habis dibagi oleh n, dan A(n) adalah nilai k tersebut yang terkecil; sebagai contoh, A(7) = 6 dan A(41) = 5.
Nilai n terkecil yang akan membuat A(n) melebihi sepuluh adalah 17.
Carilah nilai n terkecil yang akan membuat A(n) melebihi satu juta.
Answer: 82cd979a2b79600137aea54fa0bd944b
Soal 130
Sebuah bilangan yang hanya berisi angka satu disebut repunit. Kita akan mendefinisikan R(k) sebagai repunit dengan panjang k; sebagai contoh, R(6) = 111111.
Diberikan bahwa n adalah bilangan bulat positif, dan FPB(n, 10) = 1, dapat ditunjukkan bahwa selalu ada nilai k, dimana R(k) habis dibagi oleh n, dan A(n) adalah nilai k tersebut yang terkecil; sebagai contoh, A(7) = 6 dan A(41) = 5.
Diketahui bahwa untuk semua bilangan prima, p > 5, p − 1 pasti habis dibagi A(p). Sebagai contoh, saat p = 41, A(41) = 5, dan 40 adalah habis dibagi 5.
Tetapi, ternyata terdapat bilangan komposit langka, yang juga memenuhi sifat di atas; lima contoh pertama adalah 91, 259, 451, 481, dan 703.
Carilah jumlah dari dua puluh lima buah bilangan komposit n pertama, dimana
FPB(n, 10) = 1 dan n − 1 habis dibagi A(n).
Answer: 20594ea0ef7a2f4cf40d19a9b82a0beb
Soal 131
TErdapat beberapa bilangan prima p, yang jika berpasangan sebuah bilangan bulat positif n, dengan bentuk n3 + n2p akan menghasilkan bilangan kubik sempurna.
Sebagai contoh, saat p = 19, 83 + 82×19 = 123.
Luar biasanya, untuk setiap bilangan prima dengan sifat ini, terdapat nilai n yang berbeda, dan hanya terdapat empat buah bilangan prima dengan sifat ini yang kurang dari seratus.
Berapa banyak bilangan prima kurang dari satu juta yang memiliki sifat istimewa ini?
Answer: f7e6c85504ce6e82442c770f7c8606f0
Soal 132
Sebuah bilangan yang hanya berisi angka satu disebut repunit. Kita akan mendefinisikan R(k) sebagai repunit dengan panjang k.
Sebagai contoh, R(10) = 1111111111 = 11×41×271×9091, dan jumlah dari semua faktor primanya adalah 9414.
Carilah jumlah dari empat puluh faktor prima pertama dari R(109).
Answer: 5df3a36faa173a393a04a022b2d5d49d
Soal 133
Sebuah bilangan yang hanya berisi angka satu disebut repunit. Kita akan mendefinisikan R(k) sebagai repunit dengan panjang k; sebagai contoh, R(6) = 111111.
Misalkan terdapat repunit dengan bentuk R(10n).
Walaupun R(10), R(100), atau R(1000) tidak habis dibagi oleh 17, tetapi R(10000) habis dibagi oleh 17. Namun tidak ada nilai n dimana R(10n) akan habis dibagi 19. Pada kenyataannya, hanya terdapat empat buah bilangan prima kurang dari seratus 11, 17, 41, dan 73 yang dapat membagi habis R(10n).
Carilah jumlah semua bilangan prima kurang dari seratus ribu, yang tidak akan pernah dapat membagi habis bilangan R(10n).
Answer: c1d33d79d08cde65eaa78e4583ea0594
Soal 134
Misalkan terdapat bilangan prima berurutan p1 = 19 dan p2 = 23. Dapat dibuktikan bahwa 1219 adalah bilangan terkecil yang angka terakhirnya dibentuk dari p1, dan juga habis dibagi oleh p2.
Bahkan, dengan mengecualikan p1 = 3 dan p2 = 5, untuk semua pasangan bilangan prima p2 > p1, akan selalu ada sebuah bilangan n yang angka terakhirnya dibentuk darip1 dan n juga habis dibagi oleh p2. Misalkan S adalah nilai n terkecil.
Carilah ∑ S untuk semua pasangan bilangan prima dengan ketentuan 5 ≤ p1 ≤ 1000000.
Answer: f12b07460d2586ea47b4d305ae0b0539
Soal 135
Diberikan bilangan bulat positif, x, y, dan z, yang membentuk suatu barisan aritmatika, bilangan bulat positif terkecil n, untuk persamaan x2 − y2 − z2 = n, yang mempunyai persis dua solusi adalah n = 27:
342 − 272 − 202 = 122 − 92 − 62 = 27
Dapat ditemukan bahwa n = 1155 adalah nilai n terkecil yang memiliki persis sepuluh solusi.
Berapakah nilai n kurang dari satu juta yang memiliki persis sepuluh solusi berbeda?
Answer: c457d7ae48d08a6b84bc0b1b9bd7d474
Soal 136
Bilangan bulat positif, x, y, dan z, akan membentuk sebuah barisan aritmatika. Diberikan n adalah sebuah bilangan bulat positif, persamaan x2 − y2 − z2 = n, akan mempunyai persis satu solusi saat n = 20:
132 − 102 − 72 = 20
Nyatanya, terdapat dua puluh lima buah nilai n kurang dari seratus, yang akan menghasilkan solusi unik pada persamaan di atas.
Berapa banyak nilai n kurang dari lima puluh juta yang mempunyai persis satu solusi?
Answer: 91db9e8e6cb2dbf9c07a6e0429697336
Soal 137
Misalkan terdapat suku banyak tak hingga AF(x) = xF1 + x2F2 + x3F3 + ..., dimana Fk adalah suku ke-kdari barisan Fibonacci: 1, 1, 2, 3, 5, 8, ... ; yang dibentuk dengan, Fk = Fk−1 + Fk−2, F1 = 1 dan F2 = 1.
Untuk soal ini, kita hanya akan memperhatikan nilai dari x, yang memiliki nilai AF(x) berupa bilangan bulat positif.
| Secara mengejutkan AF(1/2) | = | (1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ... |
| = | 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ... | |
| = | 2 |
Nilai dari x yang akan menghasilkan lima bilangan asli pertama adalah sebagai berikut.
| x | AF(x) |
| √2−1 | 1 |
| 1/2 | 2 |
| (√13−2)/3 | 3 |
| (√89−5)/8 | 4 |
| (√34−3)/5 | 5 |
Kita akan menyebut AF(x) sebagai sebuah bongkah emas, apabila x merupakan bilangan rasional, karena semakin lama, bilangan ini akan semakin sulit ditemui; sebagai contoh, bilangan bongkah emas ke-10 adalah 74049690.
Carilah bilangan bongkah emas ke-15.
Answer: 44845aa0f47ec925a3b43e6460a55e27
Soal 138
Terdapat sebuah segitiga sama kaki dengan panjang alas b = 16, dan panjang kaki L = 17.
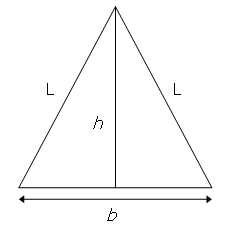
Dengan menggunakan teorema Pythagoras, dapat terlihat bahwa tinggi segitiga tersebut adalahh = √(172 − 82) = 15, dimana hanya berseleisih satu satuan dari alasnya.
Dengan b = 272 dan L = 305, kita bisa mendapatkan h = 273, dimana hanya berselisih satu satuan dari alasnya, dan ini adalah segitiga terkecil kedua yang memiliki sifat h = b ± 1.
Carilah ∑ L untuk dua belas segitiga sama kaki terkecil pertama, dimana h = b ± 1 dan b, L adalah bilangan bulat positif.
Answer: f7524f4d0d6d042c0f92a0d6469aff85
Soal 139
Misalkan (a, b, c) adalah ketiga sisi dari sebuah segitiga siku-siku, dengan panjang sisi yang diurutkan dari kecil ke besar. Kita dapat mengumpulkan empat buah segitiga tersebut bersama-sama untuk membentuk suatu persegi dengan panjang sisi c.
Sebagai contoh, segitiga (3, 4, 5) dapat diletakkan bersama-sama untuk membentuk persegi dengan ukuran 5 x 5, dengan sebuah lubang persegi berukuran 1 x 1 di tengahnya. Dan dapat terlihat bahwa persegi berukuran 5 x 5 tersebut dapat ditutup oleh dua puluh lima ubin persegi berukuran 1 x 1.
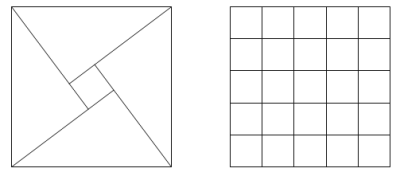
Tetapi, jika segitiga (5, 12, 13) digunakan, maka akan terdapat lubang berukuran 7 x 7, dan segitiga tersebut tidak bisa digunakan untuk membuat persegi dengan ukuran 13 x 13.
Diketahui keliling dari suatu segitiga siku-siku adalah kurang dari satu juta satuan panjang, berapa banyak segitiga siku-siku yang dapat digunakan untuk membentuk persegi besar seperti contoh di atas?
Answer: 1c343ba00e6d17d7239bf45869ffed0c
Soal 140
Misalkan terdapat suku banyak tak hingga AG(x) = xG1 + x2G2 + x3G3 + ..., dimana Gk adalah suku ke-k dari suatu barisan yang dibentuk dengan Gk = Gk−1 + Gk−2, G1 = 1 dan G2 = 4; barisan tersebut adalah, 1, 4, 5, 9, 14, 23, ... .
Untuk soal ini, kita hanya akan memperhatikan nilai dari x, yang memiliki nilai AF(x) berupa bilangan bulat positif.
Nilai dari x yang akan menghasilkan lima bilangan asli pertama adalah sebagai berikut.
| x | AG(x) |
| (√5−1)/4 | 1 |
| 2/5 | 2 |
| (√22−2)/6 | 3 |
| (√137−5)/14 | 4 |
| 1/2 | 5 |
Kita akan menyebut AF(x) sebagai sebuah bongkah emas, apabila x merupakan bilangan rasional, karena semakin lama, bilangan ini akan semakin sulit ditemui; sebagai contoh, bilangan bongkah emas ke-20 adalah 211345365.
Carilah jumlah dari semua tiga puluh bilangan bongkah emas pertama.
Answer: e5d75f96929ba250b2732aad52f3028c
Soal 141
Sebuah bilangan bulat positif n, dibagi oleh d dan menghasilkan hasil bagi (quotient) dan sisa (remainder) masing-masing q dan r. Lalu d, q, dan r adalah bilangan bulat positif yang dapat membentuk barisan geometri, namun tidak harus dengan urutan demikian.
Sebagai contoh, 58 dibagi oleh 6 memiliki hasil 9 dan sisa 4. dapat terlihat bahwa 4, 6, 9 adalah suku berurutan dalam suatu barisan geometri (dengan rasio 3/2).
Kita akan menyebut bilangan n tersebut sebagai bilangan progresif.
Beberapa bilangan progresif, seperti 9 dan 10404 = 1022, terkadang juga merupakan bilangan kuadrat.
Jumlah dari semua bilangan progresif yang juga merupakan bilangan kuadrat kurang dari seratus ribu adalah 124657.
Carilah jumlah semua bilangan progresif yang juga merupakan bilangan kuadrat kurang dari satu triliun (1012).
Answer: 2aaefa1db80951be140183f9e8c0194e
Soal 142
Carilah nilai x + y + z terkecil, dengan syarat x > y > z > 0, dan x, y, dan z adalah bilangan bulat, sehingga x + y, x − y, x + z, x − z, y + z, y − z semuanya adalah bilangan kuadrat sempurna.
Answer: d3de282705508407532aa20ca8928e3b
Soal 143
Misalkan terdapat sebuah segitiga ABC dengan besar semua sisi bagian dalamnya kurang dari 120 derajat. Misalkan X adalah titik yang terletak di dalam segitiga tersebut, dan misalkan XA = p, XC = q, dan XB = r.
Fermat pernah menantang Torricelli untuk mencari posisi X saat p + q + r memiliki nilai sekecil mungkin.
Torricelli dapat membuktikan, bahwa jika segitiga sama sisi AOB, BNC dan AMC digambarkan pada setiap sisi segitiga ABC, lingkaran luar dari segitiga AOB, BNC, dan AMC akan berpotongan di satu titik T, di dalam segitiga. Kemudian ia membuktikan bahwa T, yang disebut titik Torricelli/Fermat, mempunyai nilai p + q + r terkecil. Bahkan lebih luar biasanya lagi, dapat dibuktikan bahwa saat hasil penjumlahan dibuat sekecil mungkin, AN = BM = CO = p + q + r dan AN, BM serta CO juga saling berpotongan pada titik T.
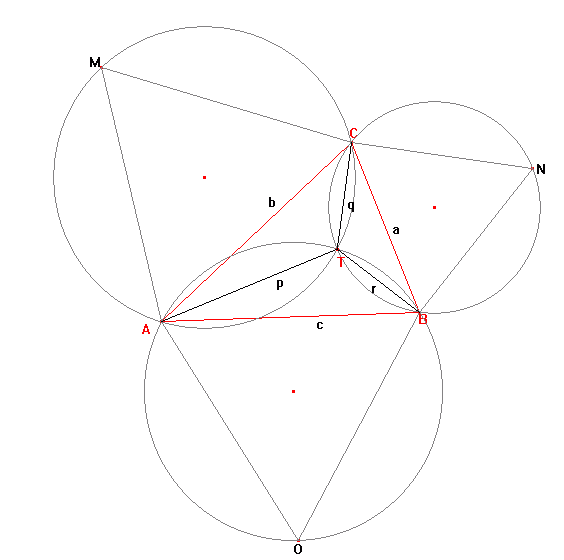
Jika hasil penjumlahan telah dibuat sekecil mungkin dan a, b, c, p, q serta r semuanya adalah bilangan bulat positif, kita akan menyebut segitiga ABC sebagai segitiga Torricelli. Sebagai contoh, a = 399, b = 455, c = 511 adalah salah satu contoh dari segitiga Torricelli triangle, dengan p + q + r = 784.
Carilah jumlah semua hasil berbeda dari p + q + r ≤ 120000 untuk segitiga Torricelli.
Answer: ec2d4c1a0c204d1f06ea5e2d189034f6
Soal 144
Dalam ilmu fisika tentang laser, sebuah "white cell" adalah sebuah sistem cermin yang bertindak untuk menunda jalannya sinar laser. Saat sinar memasuki cell, sinar akan memantul di dalam cell, sampai sinar tersebut berhasil kembali keluar.
Sebuah white cell akan kita anggap memiliki bentuk elips dengan persamaan 4x2 + y2 = 100
Bagian pada interval −0.01 ≤ x ≤ +0.01 di sebelah atas adalah kosong, sehingga memungkinkan sinar untuk masuk dan keluar dari lubang tersebut.
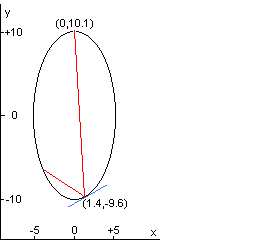
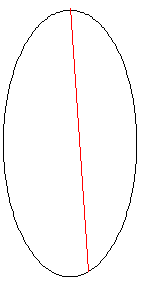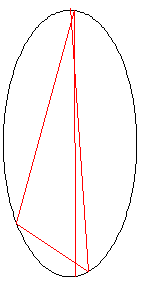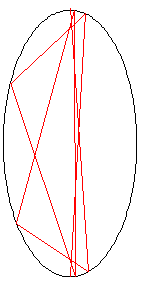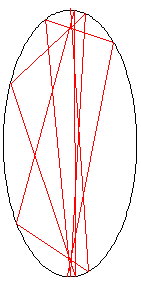
Sinar pada soal ini mulai bergerak dari titik (0.0,10.1) di luar white cell, dan sinar pertama kali menabrak dinding cell di (1.4,-9.6).
Setiap kali sinar laser menabrak permukaan elips, sinar tersebut akan mengikuti hukum pemantulan pada fisika "sudut datang sama dengan sudut pandul." Sehingga, kedua sudut, baik sudut datang maupun sudut pantul akan memiliki besar sudut yang sama pada titik pemantulan cermin.
Pada gambar di sebelah kiri, garis merah menunjukkan dua titik kontak pertama antara sinar laser dengan dinding white cell; garis biru menunjukkan garis singgung pada sebuah titik di elips yang merupakan titik pemantulan pertama.
Kemiringan atau gradien m dari garis singgung pada titik (x,y) apapun yang menyinggung elips adalah: m = −4x/y
Garis normal yang ada adalah tegak lurus dengan garis singgung ini, dan berpotongan pada titik pantul.
Animasi di sebelah kanan akan menunjukkan 10 pemantulan pertama sinar laser.
Berapa kali sinar menabrak permukaan dalam white cell sampai akhirnya berhasil keluar?
Answer: 8dd48d6a2e2cad213179a3992c0be53c
Soal 145
Beberapa bilangan bulat positif n memiliki hasil penjumlahan [ n + kebalikan(n) ] yang berisi angka-angka ganjil. Sebagai contoh, 36 + 63 = 99 dan 409 + 904 = 1313. Kita akan menyebut bilangan tersebut sebagai bilangan reversible; sehingga 36, 63, 409, dan 904 adalah reversible. Angka nol di awal tidak diperbolehkan, baik pada n maupun pada kebalikan (n).
Terdapat 120 buah bilangan reversible kurang dari seribu.
Berapa banyak bilangan reversible kurang dari satu milliar (109)?
Answer: 705e8444ad9c92e9a7589fb97515a9b6
Soal 146
Bilangan bulat terkecil n yang dapat menghasilkan n2+1, n2+3, n2+7, n2+9, n2+13, dan n2+27 berupa bilangan prima berurutan adalah n=10. Jumlah semua bilangan n kurang dari satu juta adalah 1242490.
Berapakah jumlah semua bilangan bulat n yang memiliki sifat serupa yang kurang dari 150 juta?
Answer: 525bd2bf0e31b0f19b38a1d21f2f6a16
Soal 147
Pada kotak-kotak bersilang berukuran 3x2, terdapat sebanyak 37 persegi panjang berbeda yang dapat dibuat mengikuti garis yang ada seperti terlihat pada gambar.
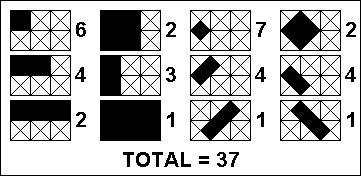
Terdapat 5 ukuran kotak-kotak bersilang lain yang lebih keci dari 3x2, yaitu 1x1, 2x1, 3x1, 1x2 dan 2x2. Jika setiap kotak-kotak bersilang tersebut dicari jumlah persegi panjangnya, maka akan didapat jumlah persegi panjang sebagai berikut:
1x1: 1
2x1: 4
3x1: 8
1x2: 4
2x2: 18
Dengan menambahkan angka di atas dengan 37 dari kotak-kotak ukuran 3x2, maka kita akan mendapatkan sebayak 72 persegi panjang berbeda yang dapat dibuat dari kotak-kotak bersilang berukuran kurang dari atau sama dengan 3x2.
Berapa banyak persegi panjang yang dapat dibuat dari kotak-kotak bersilang berukuran kurang dari atau sama dengan 47x43?
Answer: d0fca7d85d4a4df043a2ae5772ea472e
Soal 148
Kita dapat dengan mudah membuktikan bahwa tidak ada satupun bilangan pada tujuh baris pertama segitiga pascal yang habis dibagi 7:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Tetapi, apabila kita memeriksa seratus baris pertama, kita akan menemukan bahwa hanya terdapat 2361 bilangan dari 5050 bilangan y ang ada yang tidak habis dibagi 7.
Carilah berapakah banyaknya bilangan yang tidak habis dibagi 7 pada satu miliar (109) baris pertama segitiga Pascal.
Answer: 8a631ab4e3d06baf88299bf4e501b837
Soal 149
Dengan melihat tabel berikut ini, dapat dengan mudah dibuktikan bahwa hasil penjumlahan terbesar dari bilangan-bilangan dalam satu garis lurus ke segala arah (horizontal, vertikal, diagonal atau anti-diagonal) adalah 16 (= 8 + 7 + 1).
┌────┬────┬────┬─────┐
│ −2 │ 5 │ 3 │ 2 │
├────┼────┼────┼─────┤
│ 9 │ −6 │ 5 │ 1 │
├────┼────┼────┼─────┤
│ 3 │ 2 │ 7 │ 3 │
├────┼────┼────┼─────┤
│ −1 │ 8 │ −4 │ 8 │
└────┴────┴────┴─────┘
Sekarang, mari kita mengulang proses pencarian, namun dalam skala yang lebih besar:
Pertama-tama, buatlah empat juta bilangan acak dengan sebuah teknik yang disebut sebagai "Lagged Fibonacci Generator":
Untuk 1 ≤ k ≤ 55, sk = [100003 − 200003k + 300007k3] (modulo 1000000) − 500000.
Untuk 56 ≤ k ≤ 4000000, sk = [sk−24 + sk−55 + 1000000] (modulo 1000000) − 500000.
Sehingga, s10 = −393027 dan s100 = 86613.
Bilangan-bilangan s tersebut kemudian disusun dalam tabel berukuran 2000×2000, menggunakan 2000 bilangan pertama untuk mengisi baris pertama (secara berurutan), lalu 2000 bilangan selanjutnya untuk mengisi baris kedua, dan seterusnya.
Akhirnya, carilah jumlah bilangan terbesar dalam satu garis lurus ke segalah arah (horizontal, vertikal, diagonal atau anti-diagonal).
Answer: 96affc386f4b786c2521a32944424982
Soal 150
Pada suatu barisan bilangan berbentuk segitiga, terdapat bilangan bulat positif dan negatif, kita akan mencari sebuah segitiga yang lebih kecil, yang akan memuat bilangan-bilangan yang memiliki hasil penjumlahan sekecil mungkin.
Pada contoh berikut ini, kita dapat dengan mudah membuktikan bahwa segitiga yang ditandai memiliki hasil penjumlahan −42.
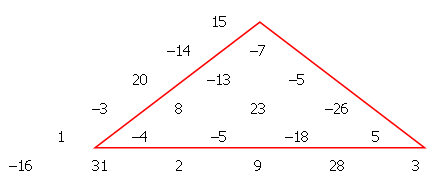
Kita akan membuat barisan bilangan berbentuk segitiga seperti di atas, namun dengan seratus buah baris, sehingga kita akan membuat 500500 buah angka acak sk pada rentang ±219, menggunakan sebuah alat pembentuk angka acak (yang dikenal sebagai Linear Congruential Generator) sebagai berikut:
t := 0
for k = 1 up to k = 500500:
t := (615949*t + 797807) modulo 220
sk := t−219
Sehingga: s1 = 273519, s2 = −153582, s3 = 450905 etc
Kemudian kita akan membentuk barisan bilangan berbentuk segitiga, dengan bilangan-bilangan acak tersebut:
s2 s3
s4 s5 s6
s7 s8 s9 s10
...
Segitiga kecil yang akan kita pilih boleh dimulai dari mana saja pada segitiga besar, dan boleh memiliki tinggi berapapun sesuka kita (pada puncak segitiga, kita dapat mengambil dua bilangan di bawahnya, lalu kemudian tiga bilangan di bawahnya, dan seterusnya).
"Hasil penjumlahan dari segitiga kecil" didapatkan dengan cara menjumlahkan semua anggota yang terdapat di dalam segitiga kecil tersebut.
Carilah hasil penjumlahan terkecil dari bilangan-bilangan yang terdapat dalam segitiga kecil.
Answer: 1802939e514020769701c59b422c0498
Soal 151
Sebuah tempat percetakan mengerjakan 16 pekerjaan setiap minggu, dan setiap pekerjaan memerlukan selembar kertas pemeriksa warna dengan ukuran A5.
Setiap Senin pagi, kepala tempat percetakan membuka amplop baru, yang berisi selembar kertas pemeriksa warna besar berukuran A1.
Ia memotong kertas itu menjadi dua bagian sama besar, sehingga terdapat dua lembar kertas berukuran A2. Kemudian dia memotong lagi salah satu dari kertas tersebut menjadi dua, sehingga didapat dua lembar kertas berukuran A3, dan begitu seterusnya sampai ia mendapat kertas berukuran A5 yang ia perlukan untuk mengerjakan pekerjaan pertama di awal minggu.
Semua kertas yang tidak terpakai dikembalikan ke dalam amplop.
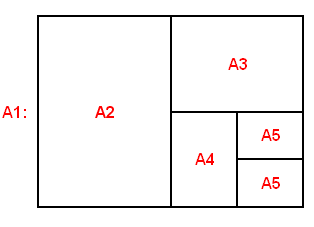
Saat awal dari setiap pekerjaan, ia mengambil kertas dari amplop secara acak. Jika kertas tersebut sudah berukuran A5, maka langsung ia gunakan. Tetapi apabila ia mendapat kertas yang lebih besar, ia akan melakukan proses pemotongan kembali, sampai ia mendapatkan ukuran kertas yang diperlukan, dan kembali menaruh sisanya ke dalam amplop.
Dengan mengabaikan pekerjaan pertama dan terakhir dalam setiap minggu, carilah perkiraan berapa kali kepala tempat percetakan tersebut hanya menemukan selembar kertas di dalam amplop (untuk setiap minggunya).
Berikan jawaban anda yang dibulatkan enam angka di belakang koma dengan format x.xxxxxx .
Answer: fb84a530fa9a8199edfadd618727fb70
Soal 152
Terdapat beberapa cara untuk menulis bilangan 1/2 sebagai hasil penjumlahan bilangan kebalikan kuadrat berbeda.
Sebagai contoh, bilangan {2,3,4,5,7,12,15,20,28,35} dapat digunakan dengan cara:
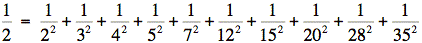
Kenyataannya, hanya dengan menggunakan bilangan bulat antara 2 sampai 45, terdapat tiga cara untuk melakukan hal yang sama seperti di atas, dua cara lainnya adalah: {2,3,4,6,7,9,10,20,28,35,36,45} dan {2,3,4,6,7,9,12,15,28,30,35,36,45}.
Berapa banyaknya cara untuk menulis bilangan 1/2 sebagai hasil penjumlahan bilangan kebalikan kuadrat, dengan menggunakan bilangan bulat berbeda antara 2 dan 80?
Answer: 34ed066df378efacc9b924ec161e7639
Soal 153
Seperti yang kita ketahui, persamaan x2=-1 tidak mempunyai solusi untuk x bilangan real.
Namun apabila kita mengenalkan bilangan imajiner i, persamaan ini akan memiliki dua solusi: x=i dan x=-i.
Jika kita melangkah lebih jauh, persamaan (x-3)2=-4 memiliki dua solusi bilangan kompleks: x=3+2i dan x=3-2i.
x=3+2i dan x=3-2i keduanya akan disebut konjugat kompleks.
Semua bilangan yang berbentuk a+bi akan disebut sebagai bilangan kompleks.
Secara umum a+bi dan a−bi adalah pasangan konjugat kompleks.
Bilangan bulat Gaussian adalah sebuah bilangan kompleks a+bi yang nilai a dan b nya merupakan bilangan bulat.
Bilangan bulat yang biasa kita gunakan juga merupakan bilangan bulat Gaussian (dengan nilai b=0).
Untuk membedakannya, maka bilangan bulat Gaussian dengan b ≠ 0 akan kita sebut sebagai "bilangan bulat rasional."
Sebuah bilangan bulat Gaussian akan disebut pembagi dari bilangan bulat rasional n, apabila hasil pembagiannya juga merupakan bilangan bulat Gaussian.
Sebagai contoh, kita akan membagi 5 dengan 1+2i, kita dapat mengerjakan 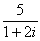 dengan cara sebagai berikut:
dengan cara sebagai berikut:
Kalikan pembilang dan penyebut dengan konjugat kompleks dari 1+2i: yaitu 1−2i.
Hasilnya adalah
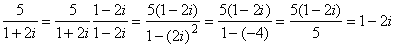 .
.
Sehingga 1+2i adalah merupakan pembagi dari 5.
Perlu diingat bahwa 1+i bukanlah pembagi dari 5 karena 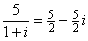 .
.
Perlu diingat juga bahwa jika sebuah bilangan bulat Gaussian (a+bi) merupakan pembagi dari suatu bilangan bulat rasional n, maka konjugat kompleksnya (a−bi) juga merupakan pembagi dari n.
Pada kenyataannya, 5 memiliki enam buah pembagi yang memiliki bagian real a positif: {1, 1 + 2i, 1 − 2i, 2 + i, 2 − i, 5}.
Tabel berikut ini berisi semua pembagi dari lima bilangan bulat rasional positif pertama:
| n | Pembagi bilangan bulat Gaussian dengan bagian real a positif | Banyaknya s(n) dari pembagi tersebut |
| 1 | 1 | 1 |
| 2 | 1, 1+i, 1-i, 2 | 5 |
| 3 | 1, 3 | 4 |
| 4 | 1, 1+i, 1-i, 2, 2+2i, 2-2i,4 | 13 |
| 5 | 1, 1+2i, 1-2i, 2+i, 2-i, 5 | 12 |
Untuk pembagi dengan bagian real a positif, kita bisa mendapatkan:
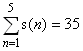
Untuk 1 ≤ n ≤ 105, ∑ s(n)=17924657155.
Berapakah ∑ s(n) untuk 1 ≤ n ≤ 108?
Answer: 08ec9d6e6c2275d37e7a227fb2d1f06f
Soal 154
Sebuah piramida/limas segitiga dibuat menggunakan bola-bola, sehingga setiap bola bersandar pada tiga buah bola di bawahnya.
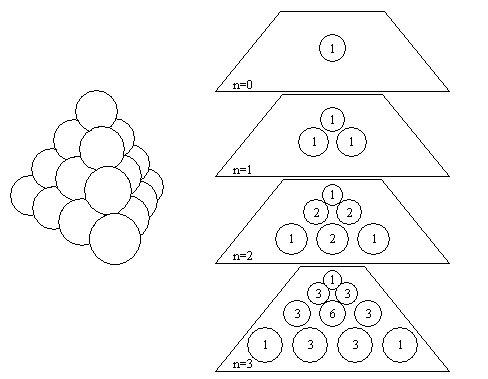
Lalu kita akan menghitung banyaknya jalur dari puncak piramida ke setiap posisi:
Setiap jalur dimulai dari puncak piramida, dan turun salah satu dari tiga bolah yang ada di bawahnya.
Akibatnya, banyaknya jalur yang diperlukan untuk sampai ke posisi tertentu bisa didapatkan dengan menjumlahkan bilangan bola-bola di atas bola tersebut (tergantung posisi bola, kita mungkin bisa menjumlahkan bilangan maksimal sampai tiga buah bola di atasnya).
Hasilnya, akan terbentuk piramida Pascal, dan bilangan-bilangan pada setiap tingkat n merupakan koefisien dari penjabaran (x + y + z)n.
Berapa banyak koefisien pada penjabaran (x + y + z)200000 yang merupakan kelipatan 1012?
Answer: de866633fa075beb3897cbbc8abf2400
Soal 155
Sebuah rangkaian listrik menggunakan kapasitor yang sama, yang memiiki kapasitansi C.
Kapasitor dapat dihubungkan baik secara seri ataupun pararel untuk membentuk sub-rangkaian, sub-rangkaian dapat juga dihubungkan secara seri atau pararel dengan kapasitor lain atau dengan sub-rangkaian lain untuk membentuk sub-rangkaian yang lebih besar, dan seterusnya sampai membentuk rangkaian final.
Dengan menggunakan prosedur sederhana ini, dan jika tersedia sampai sebanyak n kapasitor identik, kita dapat membuat rangkaian yang memiliki nilai kapasitansi berbeda-beda. Sebagai contoh, dengan menggunakan maksimal sebanyak n=3 kapasitor dengan kapasitansi 60 μF pada tiap kapastiornya, kita bisa mendapatkan tujuh nilai kapasitansi berbeda:
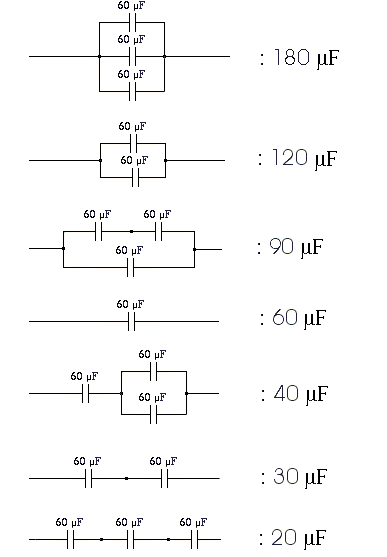
Jika kita lambangkan D(n) sebagai banyaknya nilai kapasitansi berbeda yang bisa didapatkan saat disediakan sebanyak n buah kapasitor berkapasitansi sama, sesuai dengan prosedur di atas, kita akan mendapatkan: D(1)=1, D(2)=3, D(3)=7 ...
Carilah D(18).
Catatan : Saat menghubungkan kapastior C1, C2 dan seterusnya secara pararel, total kapasitansinya akan menjadi CT = C1 + C2 +...,
Sedangkan saat dihubungkan secara seri, nilai kapasitansi total akan mengikuti aturan:
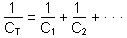
Answer: da0a3fc900cc8ae42d514e280524ee39
Soal 156
Dimulai dari nol, bilangan asli dengan basis 10 dapat ditulis sebagai berikut:
0 1 2 3 4 5 6 7 8 9 10 11 12....
Perhatikan angka d=1. Setelah kita menuliskan setiap angka n, kita akan memperhatikan banyaknya angka satu yang telah muncul, dan kita akan melambangkan hal ini dengan f(n,1). Beberapa nilai pertama dari f(n,1), adalah sebagai berikut:
| n | f(n,1) |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| 10 | 2 |
| 11 | 4 |
| 12 | 5 |
Perhatikan bahwa f(n,1) tidak pernah bernilai 3.
Dua solusi pertama dari persamaan f(n,1)=n adalah n=0 dan n=1. Kemudian solusi selanjutnya adalah n=199981.
Dengan cara yang sama, fungsi f(n,d) memberikan banyaknya angka d yang telah muncul setelah bilangan n muncul.
Pada kenyataannya, untuk semua angka d ≠ 0, 0 selalu menjadi solusi pertama dari persamaan f(n,d)=n.
Misalkan s(d) adalah hasil penjumlahan dari semua solusi yang memenuhi f(n,d)=n.
Diketahui bahwa s(1)=22786974071.
Carilah ∑ s(d) untuk 1 ≤ d ≤ 9.
Catatan: Jika terdapat nilai n yang sama, yang memenuhi f(n,d)=n untuk nilai d yang berbeda, maka nilai n ini harus ikut dihitung kembali secara terpisah, untuk setiap nilai d yang ada.
Answer: ac0c6b67ed28cebb02b802e7a204aaee
Soal 157
Misalkan terdapat sebuah persamaan diophantine 1/a+1/b= p/10n dengan a, b, p, n merupakan bilangan bulat positif dan a ≤ b.
Untuk n=1 persamaan ini memiliki 20 solusi, yaitu sebagai berikut:
| 1/1+1/1=20/10 | 1/1+1/2=15/10 | 1/1+1/5=12/10 | 1/1+1/10=11/10 | 1/2+1/2=10/10 |
| 1/2+1/5=7/10 | 1/2+1/10=6/10 | 1/3+1/6=5/10 | 1/3+1/15=4/10 | 1/4+1/4=5/10 |
| 1/4+1/20=3/10 | 1/5+1/5=4/10 | 1/5+1/10=3/10 | 1/6+1/30=2/10 | 1/10+1/10=2/10 |
| 1/11+1/110=1/10 | 1/12+1/60=1/10 | 1/14+1/35=1/10 | 1/15+1/30=1/10 | 1/20+1/20=1/10 |
Berapakah banyaknya solusi yang dimiliki persamaan tersebut untuk 1 ≤ n ≤ 9?
Answer: c96fc71df4ef8f6420fda7958957538c
Soal 158
Dengan memilih tiga huruf acak dari 26 huruf yang ada di alfabet, kita dapat membentuk tulisan dengan panjang tiga karakter.
Contohnya adalah 'abc', 'hat' dan 'zyx'.
Saat kita mempelajari ketiga contoh ini, kita dapat melihat bahwa untuk 'abc' dua huruf yang ada muncul sesuai dengan urutan pada abjad bedasarkan huruf sebelah kirinya.
Sedangkan untuk 'hat' hanya terdapat satu huruf yang sesuai dengan urutan abjad, jika dibandingkan dengan huruf di sebelah kirinya. Untuk 'zyx' tidak terdapat huruf yang sesuai dengan urutan abjad, jika dibandingkan dengan huruf di sebelah kirinya.
Pada semua kemungkinan yang ada, terdapat 10400 buah tulisan yang dibentuk oleh 3 huruf, yang memiliki persis satu buah huruf yang sesuai urutan abjad, jika dibandingkan dengan huruf di sebelah kirinya.
Misalkan terdapat tulisan dengan n ≤ 26 karakter berbeda dari alfabet.
Untuk setiap n, p(n) adalah banyaknya tulisan yang dibentuk oleh n huruf, dimana terdapat persis satu buah huruf yang sesuai urutan abjad, jika dibandingkan dengan huruf di sebelah kirinya.
Berapakah nilai terbesar dari p(n)?
Answer: 6070fa194890e52b2989af5b542aee90
Soal 159
Sebuah bilangan komposit dapat difaktorkan dengan berbagai cara. Sebagai contoh, dengan mengabaikan perkalian dengan angka satu, bilangan 24 dapat dengan mudah difaktorkan dengan 7 cara berbeda:
24 = 2x3x4
24 = 2x2x6
24 = 4x6
24 = 3x8
24 = 2x12
24 = 24
Untuk mencari angka akar dari suatu bilangan, kita dapat menjumlahkan semua angka yang ada pada bilangan tersebut, kemudian mengulang proses tersebut sampai hasil penjumlahannya kurang dari 10. Sehingga angka akar dari 467 adalah 8.
Kita akan menyebut Angka Akar dari Penjumlahan/Digital Root Sum (DRS) sebagai hasil penjumlahan semua angka akar dari faktor-faktor suatu bilangan.
Diagram berikut akan menunjukkan semua nilai DRS untuk bilangan 24.
| Faktorisasi | Digital Root Sum |
|---|---|
2x2x2x3 |
9 |
2x3x4 |
9 |
2x2x6 |
10 |
4x6 |
10 |
3x8 |
11 |
2x12 |
5 |
24 |
6 |
Nilai DRS terbesar dari 24 adalah 11.
Fungsi mdrs(n) akan memberikan nilai DRS terbesar untuk bilangan n. Sehingga mdrs(24)=11.
Carilah ∑mdrs(n) untuk 1 < n < 1,000,000.
Answer: 2ab79df40adc1028d1fa83a6333db907
Soal 160
Untuk nilai N apapun, f(N) adalah lima angka terakhir sebelum mucnulnya angka nol berulang-ulang pada N!.
Sebagai contoh,
9! = 362880 sehingga f(9)=36288
10! = 3628800 sehingga f(10)=36288
20! = 2432902008176640000 sehingga f(20)=17664
Carilah f(1,000,000,000,000)
Answer: e51ada1e23f810eb1b51a18bb6825f85
Soal 161
Triomino adalah sebuah bentuk yang dibuat dari tiga persegi, yang disambungkan sisinya. Terdapat dua bentuk dasar:
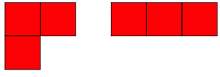
Jika semua arah hadap diperhitungkan, maka terdapat enam macam kombinasi:
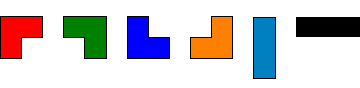
Semua persegi panjang berukuran n x m dimana nxm habis dibagi 3 dapat dibentuk oleh triominoes.
Jika hasil refleksi dan rotasi dari triomino dianggap sebagai pola yang berbeda, maka kita bisa mendapatkan 41 cara untuk membentuk persegi panjang berukuran 2 x 9 dengan triomino:
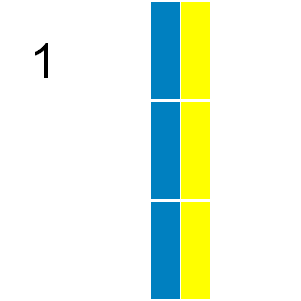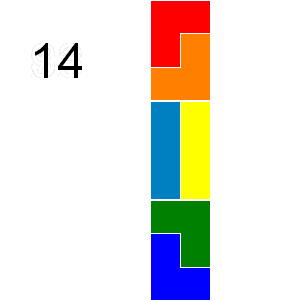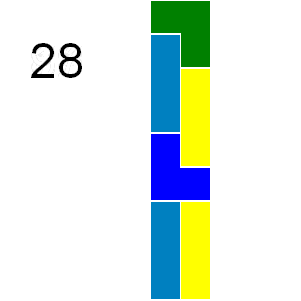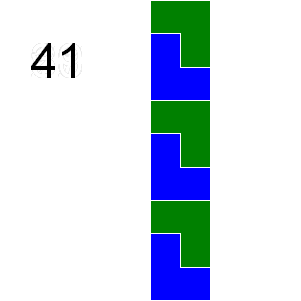
Berapakah banyaknya cara persegi panjang berukuran 9 x 12 bisa dibentuk oleh triomino?
Answer: 975ccc38bb5402c5b485f3de5928d919
Soal 162
Pada sistem bilangan heksadesimal, bilangan dituliskan dengan 16 angka berbeda:
Bilangan heksadesimal AF saat dituliskan dalam bentuk desimal sama dengan 10x16+15=175.
Pada bilangan heksadesimal 3 angka, bilangan 10A, 1A0, A10, dan A01 semuanya mempunyai angka 0,1 dan A.
Seperti bilangan yang ditulis di secara desimal, kita menulis bilangan heksadesimal tanpa angka nol di depan.
Berapa banyak bilangan heksadesimal yang dibentuk dari paling banyak enam belas angka, yang angka 0, 1, dan A nya muncul setidaknya satu kali?
Berikan jawaban Anda dalam bilangan heksadesimal.
(A,B,C,D,E dan F harus ditulis dengan huruf kapital, tanpa perlu ditandai bahwa bilangan tersebut adalah bilangan heksadesimal, dan tidak diawali dengan angka nol, sebagai contoh 1A3F adalah penulisan yang benar, dan bukan: 1a3f dan bukan 0x1a3f juga bukan $1A3F juga bukan #1A3F dan bukan 0000001A3F)
Answer: 049419b9fdad9af74d5888626fff56a3
Soal 163
Misalkan terdapat sebuah segitiga sama sisi, dan digambarkan sebuah garis lurus dari semua titik pada segitiga ke tengah-tengah sisi di seberangnya, seperti pada gambar size 1 berikut ini.
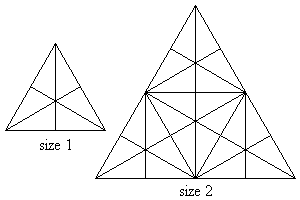
Sekarang enam belas segitiga berbeda ukuran, bentuk, arah hadap, dan tempat dapat ditemukan pada segitiga ini. Menggunakan segitiga size 1 sebagai segitiga pembangun, kita dapat membentuk segitiga yang lebih besar, salah satunya adalah segitiga size 2 pada gambar di atas. Sekarang kita dapat melihat bahwa terdapat seratus empat buah segitiga berbeda, jika kita mengamati segitiga size 2.
Dapat terlihat bahwa segitiga size 2 dibentuk dari 4 buah segitiga size 1. Sebuah segitiga size 3 nantinya akan berisi 9 buah segitiga size 1 dan segitiga dengan ukuran size n akan berisi n2 buah segitiga size 1.
Jika kita melambangkan T(n) sebagai banyaknya segitiga yang dapat diamati dari segitiga dengan ukuran size n, maka
T(1) = 16
T(2) = 104
Carilah T(36).
Answer: a4f66a42a5b5dc395d00463d77e0a0c6
Soal 164
Berapakah banyaknya bilangan 20-angka n (tidak diawali dengan angka nol) yang ada, sehingga tidak ada tiga angka berurutan pada n yang memiliki jumlah lebih dari 9?
Answer: 6e96debf3bfe7cc132401bafe5a5d6d6
Soal 165
Sebuah segmen garis ditentukan oleh dua titik ujungnya.
Apabila terdapat dua segmen garis dalam sebuah bidang geometri, maka terdapat tiga kemungkinan:
kedua segmen tidak bertemu di titik manapun, bertemu di satu titik, atau bertemu di tak hingga buah titik.
Selanjutnya, saat dua segmen garis bertemu di satu titik, ada kemungkinan titik temu tersebut merupakan ujung dari salah satu segmen, atau bahkan ujung dari kedua segmen. Jika titik temu kedua segmen garis bukan merupakan ujung dari kedua segmen, maka kita akan menyebut titik tersebut sebagai titik interior segmen.
Kita akan menyebut titik temu T antara dua segmen L1 dan L2 sebagai titik potong sejati dari L1 dan L2 apabila T merupakan salah satu titik yang terdapat pada L1 dan L2, dan T merupakan titik interior dari kedua segmen.
Misalkan terdapat tiga segmen garis L1, L2, dan L3:
L1: (27, 44) sampai (12, 32)
L2: (46, 53) sampai (17, 62)
L3: (46, 70) sampai (22, 40)
Dapat dibuktikan bahwa segmen garis L2 dan L3 mempunyai sebuah titik potong sejati. Perlu diingat bahwa walaupun titik ujung dari L3: (22,40) terdapat pada L1, tapi titik ini tidak dianggap sebagai titik potong sejati. Sedangkan L1 dan L2 tidak memiliki titik temu sama sekali. Sehingga antar ketiga segmen garis tersebut, kita bisa menemukan satu titik potong sejati.
Sekarang kita akan melakukan hal yang sama untuk 5000 segmen garis. Kita akan membuat 20000 bilangan menggunakan metode "Blum Blum Shub", sebuah metode untuk membentuk bilangan acak.
s0 = 290797
sn+1 = sn×sn (modulo 50515093)
tn = sn (modulo 500)
Untuk membuat sebuah segmen garis, kita akan menggunakan empat bilangan berurutan tn. Sehingga, segmen garis pertama yang ada adalah:
(t1, t2) to (t3, t4)
Empat bilangan pertama yang dibuat secara acak dengan cara di atas adalah: 27, 144, 12 dan 232. Sehingga segmen garis pertamanya akan menjadi (27,144) sampai (12,232).
Berapakah banyaknya titik potong sejati berbeda, yang terdapat pada 5000 segmen garis tersebut?
Answer: b87b096af5a545b4f7a45cfed4e67c87
Soal 166
Sebuah kotak-kotak berukuran 4x4 diisi dengan angka d, 0 ≤ d ≤ 9.
Dapat terlihat pada kotak-kotak
6 3 3 0
5 0 4 3
0 7 1 4
1 2 4 5
hasil penjumlahan dari setiap baris dan kolom mempunyai nilai 12. Selanjutnya, jumlah dari setiap diagonal juga 12.
Berapakah banyaknya cara kita bisa mengisi kotak-kotak berukuran 4x4, dengan angka d, 0 ≤ d ≤ 9 sehingga setiap baris, kolom, dan diagonal memiliki jumlah yang sama?
Answer: e4f39f61ee7f1bfe433a177c07f5512f
Soal 167
Untuk dua bilangan bulat positif a dan b, sebuah barisan Ulam U(a,b) dinyatakan oleh U(a,b)1 = a, U(a,b)2 = b dan untuk k > 2, U(a,b)k adalah bilangan bulat terkecil yang lebih besar dari U(a,b)(k-1) yang dapat ditulis sebagai hasil penjumlahan dua anggota berbeda sebelumnya pada U(a,b).
Sebagai contoh, barisan U(1,2) dimulai dengan
1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8;
5 tidak termasuk anggota barisan di atas karena 5 = 1 + 4 = 2 + 3 mempunyai dua cara untuk dibentuk dari anggota-anggota sebelumnya, sama juga seperti 7 = 1 + 6 = 3 + 4.
Carilah ∑U(2,2n+1)k untuk 2 ≤ n ≤10, dimana k = 1011.
Answer: aa5b61f6f4d96cbaeb5944b8fcdf64a3
Soal 168
Misalkan terdapat bilangan 142857. Kita dapat melakukan rotasi-kanan bilangan ini dengan memindahkan angka terakhir (7) ke depan, dan akan memberikan kepada kita bilangan 714285.
Dapat dibuktikan bahwa 714285=5×142857.
Ini menunjukkan sifat tidak biasa dari 142857: yaitu merupakan pembagi dari rotasi-kanan nya.
Carilah 5 angka terakhir dari penjumlahan semua bilangan bulat n, 10 < n < 10100, yang memiliki sifat ini.
Answer: 39e7aab76650b018578830bc6dba007a
Soal 169
Dinyatakan f(0)=1 dan f(n) adalah banyaknya cara suatu bilangan n dapat dituliskan sebagai hasil penjumlahan bilangan bulat kuadrat yang masing-masing tidak lebih dari dua kali.
Sebagai contoh, f(10)=5 karena terdapat lima cara untuk menghasilkan 10:
1 + 1 + 8
1 + 1 + 4 + 4
1 + 1 + 2 + 2 + 4
2 + 4 + 4
2 + 8
Berapakah nilai f(1025)?
Answer: d149d4836703a8908becea56ddd3ed42
Soal 170
Kita ambil angka 6, lalu kita kalikan dengan 1273 dan 9854, maka akan didapat:
6 × 1273 = 7638
6 × 9854 = 59124
Dengan menyatukan kedua hasil kali tersebut, kita akan mendapatkan bilangan pandigital 1 sampai 9, yaitu 763859124. Kita akan menyebut 763859124 sebagai “Hasil penyatuan perkalian dari 6 dan (1273,9854)”. Perlu diingat, bahwa hasil penggabungan dari bilangan-bilangan awalnya, yaitu 612739854, juga merupakan bilangan pandigital 1 sampai 9.
Hal yang sama bisa dilakukan untuk bilangan pandigital 0 sampai 9.
Berapakah bilangan pandigital 10-angka terbesar dari 0 sampai 9, yang dibentuk dengan cara menyatukan hasil perkalian suatu bilangan bulat dengan dua atau lebih bilangan bulat lainnya, dan bilangan bulat awal yang digunakan juga merupakan bilangan pandigital 10-angka dari 0 sampai 9?
Answer: 6ffe65352f717c1731666a107ace96c1
Soal 171
Untuk bilangan bulat postif n, f(n) adalah hasil penjumlahan dari kuadrat angka-angka pada bilangan n, Sebagai contoh
f(3) = 32 = 9,
f(25) = 22 + 52 = 4 + 25 = 29,
f(442) = 42 + 42 + 22 = 16 + 16 + 4 = 36
Carilah sembilan angka terakhir dari penjumlahan semua n, 0 < n < 1020, yang f(n) nya adalah berupa bilangan kuadrat.
Answer: ff586db8c4a5699ec78c645fcb27db7b
Soal 172
Berapa banyak bilangan 18-angka n (yang tidak diawali dengan angka nol) yang semua angka-angkanya tidak ada yang muncul lebih dari tiga kali?
Answer: f5f260ee21ead7478403c2ccd18a1829
Soal 173
Kita akan membuat sebuah bidang berbentuk persegi dengan "lubang" berbentuk persegi di tengahnya, sehingga bidang tersebut simetris secara vertikal maupun horizontal. Sebagai contoh, menggunakan persis tiga puluh dua ubin persegi, kita bisa membentuk dua macam bidang yang berbeda:
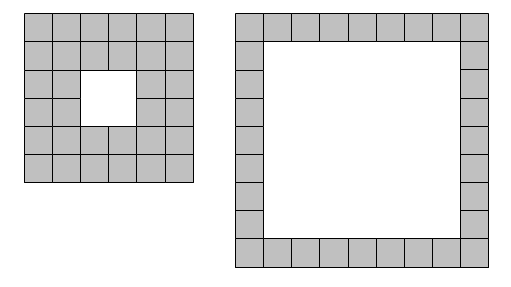
Dengan seratus buah ubin, dan Anda tidak diharuskan untuk menggunakan semua ubin, Anda dapat membentuk empat puluh satu bidang berbeda.
Jika disediakan satu juta buah ubin, berapa banyak cara bidang persegi seperti di atas yang dapat dibentuk?
Answer: 177f825c89a68aefae37b8dec9bb8a9b
Soal 174
Kita akan membuat sebuah bidang berbentuk persegi dengan "lubang" berbentuk persegi di tengahnya, sehingga bidang tersebut simetris secara vertikal maupun horizontal.
Jika diberikan delapan buah ubin persegi, maka kita hanya dapat membentuk bidang dengan satu cara: yaitu bidang yang berukuran 3x3 dengan lubang berukuran 1x1 di tengahnya. Tetapi, menggunakan tiga puluh dua ubin, kita dapat membentuk dua bidang berbeda.

Jika t melambangkan banyaknya ubin yang digunakan, kita dapat mengatakan bahwa t = 8 adalah bidang tipe L(1) dan t = 32 adalah bidang tipe L(2).
Misalkan N(n) adalah banyaknya t ≤ 1000000, sehingga t akan membentuk bidang tipe L(n); sebagai contoh, N(15) = 832.
Berapakah ∑ N(n) untuk 1 ≤ n ≤ 10?
Answer: 73166006522ed7f51ed3e2ca66353b66
Soal 175
Diketahui f(0)=1 dan f(n) adalah banyaknya cara untuk menulis bilangan n sebagai hasil dari penjumlahan bilangan 2x, dimana tidak ada bilangan 2x yang muncul lebih dari dua kali.
Sebagai contoh, f(10)=5 karena terdapat lima cara berbeda untuk menyatakan 10:
10 = 8+2 = 8+1+1 = 4+4+2 = 4+2+2+1+1 = 4+4+1+1
Dapat ditunjukkan bahwa untuk setiap pecahan p/q (p>0, q>0) terdapat setidaknya satu buah bilangan bulat n, sehingga
f(n)/f(n-1)=p/q.
Sebagai contoh, bilangan n terkecil yang memenuhi f(n)/f(n-1)=13/17 adalah 241.
Bentuk biner dari 241 adalah 11110001.
Jika bilangan biner ini dibaca dari kiri ke kanan, dapat terlihat bahwa terdapat 4 buah angka satu, 3 buah angka nol, kemudian 1 buah angka satu. Kita akan menyebut 4,3,1 sebagai Shortened Binary Expansion of 241.
Carilah Shortened Binary Expansion untuk nilai n terkecil, dimana
f(n)/f(n-1)=123456789/987654321.
Berikan jawaban Anda dengan bilangan bulat yang dipisahkan dengan koma, tanpa ada spasi.
Answer: 796dddd004c3465229058072f5b4583e
Soal 176
Terdapat empat buah segitiga siku-siku dengan panjang sisi (9,12,15), (12,16,20), (5,12,13) dan (12,35,37). Semua segitiga memiliki salah satu kaki (catheti) dengan panjang 12. Dapat terlihat bahwa tidak ada segitiga siku-siku lain yang panjang sisinya berupa bilangan bulat, yang panjang salah satu kakinya (catheti) sama dengan 12.
Carilah bilangan bulat terkecil yang bisa menjadi panjang kaki (catheti) dari 47547 buah segitiga siku-siku bersisi bilangan bulat.
Answer: c47c782ebaf8cdbb60eebfa86cd0003c
Soal 177
Misalkan ABCD adalah segiempat konveks, dengan diagonal AC dan BD. Pada setiap titik sudut, setiap diagonal akan membuat sebuah sudut dengan dua buah sisi lain, sehingga akan terbentuk delapan buah sudut pada pojok segi empat.
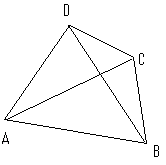
Sebagai contoh, pada titik A, terdapat dua buah sudut, yaitu CAD dan CAB.
Segi empat seperti ini, yang ke delapan sudut pada pojok segi empatnya merupakan bilangan bulat (diukur dalam derajat) akan kita sebut sebagai "Segi empat bersudut bilangan bulat". Salah satu contoh segi empat bersudut bilangan bulat adalah sebuah persegi, dimana kedelapan sudut pada pojok segiempatnya adalah 45°. Contoh lain adalah sebuah segi empat dengan sudut DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, dan ADB = 50°.
Berapakah banyaknya semua segi empat bersudut bilangan bulat?
Catatan: Dalam perhitungan Anda, Anda dapat menganggap sebuah sudut memiliki bilangan bulat, walaupun sudut tersebut masih memiliki penyimpangan sampai 10-9, atau sembilan angka di belakang koma.
Answer: d7a85236af930db0f7e84f2de8ee7ac2
Soal 178
Pada bilangan 45656.
Dapat terlihat bahwa setiap pasangan angka pada bilangan 45656 memiliki beda satu.
Sebuah bilangan yang setiap pasangan angka berurutannya memiliki beda satu disebut bilangan melangkah.
Sebuah bilangan disebut sebagai bilangan pandigital apabila bilangan tersebut memiliki semua angka dari 0 sampai 9 setidaknya sekali.
Berapa banyak bilangan melangkah pandigital kurang dari 1040 yang ada?
Answer: 2ffddfa898fa5df6321aebea84d4f33f
Soal 179
Carilah bilangan bulat 1 < n < 107, dimana n dan n + 1 memiliki banyak pembagi habis positif yang sama. Sebagai contoh, 14 memiliki pembagi habis positif empat buah, yaitu 1, 2, 7, 14 dan 15 juga memiliki pembagi positif empat buah, yaitu 1, 3, 5, dan 15.
Answer: bafa0132bc7fc422a8d53bebb9d003c9
Soal 180
Untuk bilangan bulat n, terdapat tiga buah fungsi
f1,n(x,y,z) = xn+1 + yn+1 − zn+1
f2,n(x,y,z) = (xy + yz + zx)*(xn-1 + yn-1 − zn-1)
f3,n(x,y,z) = xyz*(xn-2 + yn-2 − zn-2)
dan kombinasi ketiganya
fn(x,y,z) = f1,n(x,y,z) + f2,n(x,y,z) − f3,n(x,y,z)
Kita akan menyebut (x,y,z) sebagai bilangan triple emas dengan orde k jika x, y, dan z semuanya merupakan bilangan rasional dengan bentuk a / b dengan
0 < a < b ≤ k dan setidaknya terdapat satu bilangan bulat n, sehingga fn(x,y,z) = 0.
Misalkan s(x,y,z) = x + y + z.
Kita misalkan t = u / v sebagai hasil penjumlahan semua nilai berbeda dari s(x,y,z) untuk semua bilangan triple emas (x,y,z) dengan orde 35.
Semua s(x,y,z) dan t harus dalam bentuk paling sederhana.
Carilah u + v.
Answer: 6459f69d151314c59df404868f45fa96
Soal 181
Terdapat tiga buah benda berwarna black (hitam) B dan satu benda bewarna white (putih) W, benda-benda tersebut dapat dikelompokkan dengan 7 cara, cara-cara tersebut adalah sebagai berikut:
| (BBBW) | (B,BBW) | (B,B,BW) | (B,B,B,W) | (B,BB,W) | (BBB,W) | (BB,BW) |
Berapakah banyaknya cara enam puluh benda black (hitam) B dan empat puluh benda white (putih) W dapat dikelompokkan?
Answer: 0e1233ecbc058dabf54a8602eac55d95
Soal 182
Prosedur untuk melakukan Enkripsi RSA adalah sebagai berikut:
Buatlah dua buah angka prima berbeda p dan q.
Lalu Hitung n=pq dan φ=(p-1)(q-1).
Cari sebuah bilangan bulat e, 1<e<φ, sehingga FPB(e,φ)=1.
Sebuah pesan pada sistem ini haruslah berupa bilangan pada interval [0,n-1].
Teks yang akan dikirim harus terlebih dahulu diubah menjadi message berbentuk bilangan pada interval [0,n-1].
Untuk mengenkripsi teks, untuk tiap message m, kita harus menghitung c=me mod n.
Untuk mendekripsi teks, prosedur berikut ini yang harus dilakukan: hitunglah nilai d sehingga ed=1 mod φ, lalu untuk message yang telah dienkripsi c, hitunglah m=cd mod n.
Terdapat nilai e dan m sehingga me mod n=m.
Kita akan menyebut message m dimana me mod n=m sebagai pesan yang tidak berhasil disembunyikan.
Permasalah muncul saat kita akan memilih nilai e, yaitu nilai yang dipilih harus menyebabkan tidak terlalu banyak pesan yang tidak berhasil disembunyikan.
Sebagai contoh, misalkan p=19 dan q=37.
Maka n=19*37=703 dan φ=18*36=648.
Jika kita memilih e=181, maka walaupun FPB(181,648)=1, tapi dapat ditemukan bahwa semua messages
m (0≤m≤n-1) tidak berhasil disembunyikan saat kita menghitung me mod n.
Untuk semua nilai e pasti terdapat beberapa message yang tidak berhasil disembunyikan.
Penting bagi kita untuk membuat jumlah pesan yang tidak berhasil disembunyikan sesedikit mungkin.
Jika dipilih p=1009 dan q=3643.
Carilah jumlah semua nilai e, 1<e<φ(1009,3643) dan FPB(e,φ)=1, sehingga banyaknya message yang tidak berhasil disembunyikan oleh nilai e ini sesedikit mungkin.
Answer: 088ad9a61e60b9309e91cfc3ed27d729
Soal 183
Misalkan terdapat bilangan bulat positif N, dan misalkan N akan kita pisah menjadi k bagian sama besar, r = N/k, Sehingga N = r + r + ... + r.
Misalkan P adalah hasil kali dari semua bagian-bagian tersebut, maka P = r × r × ... × r = rk.
Sebagai contoh, jika 11 dibagi menjadi lima bagian sama besar, 11 = 2.2 + 2.2 + 2.2 + 2.2 + 2.2, maka P = 2.25 = 51.53632.
Misalkan M(N) = Pmax untuk nilai N yang diberikan.
Ternyata hasil perkalian terbesar untuk N = 11 dapat ditemukan dengan cara membagi sebelas menjadi empat bagian sama besar, yang akan menghasilkan Pmax = (11/4)4; sehingga M(11) = 14641/256 = 57.19140625, dimana hasil tersebut merupakan desimal tidak berulang.
Tetapi untuk N = 8, hasil perkalian terbesar didapatkan dengan membagi bilangan menjadi tiga bagian sama besar, sehingga M(8) = 512/27, dan hasil tersebut merupakan bilangan desimal berulang.
Diketahui D(N) = N, jika M(N) adalah bilangan desimal berulang, dan D(N) = -N jika M(N) adalah bilangan desimal yang tidak berulang.
Sebagai contoh, ΣD(N) untuk 5 ≤ N ≤ 100 adalah 2438.
Carilah ΣD(N) untuk 5 ≤ N ≤ 10000.
Answer: 438bc10af8f8eb366ec1371478ca3d3c
Soal 184
Terdapat himpunan Ir yang berisi titik-titik (x,y) yang koordinatnya berupa bilangan bulat , yang titik-titiknya berada dalam lingkaran berjari-jari r, dan berpusat di pusat koordinat, yaitu lingkaran x2 + y2 < r2.
Untuk jari-jari 2, I2 berisi sembilan titik, yaitu (0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1) dan (1,-1). Terdapat delapan segitiga yang titik-titik sudutnya merupakan anggota I2 yang sebelah dalam segitiganya terdapat pusat koordinat. Dua dari mereka ditunjukkan di gambar berikut, Segitiga lainnya bisa didapatkan dengan cara merotasikan kedua segitiga ini.
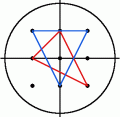
Untuk jari-jari 3, terdapat 360 segitiga yang di dalam segitiganya terdapat pusat koordinat, dan titik-titik sudutnya merupakan anggota I3. Lalu untuk I5 banyaknya segitiga serupa adalah 10600.
Berapakah banyaknya segitiga yang sebelah dalamnya terdapat pusat koordinat, dan ketiga sisinya merupakan anggota himpunan I105?
Answer: aa80f8619ed594e5d7852564457dbca6
Soal 185
Number Mind adalah salah satu bagian dari permaian populer Master Mind.
Anda diharuskan untuk menebak urutan angka-angka. Setiap kali melakukan tebakan, Anda hanya akan diberi tahu berapa buah angka yang benar Anda tebak. Sehingga, jika bilangan yang harus ditebak adalah 1234, dan Anda menebak 2036, Anda akan diberi tahu bahwa Anda berhasil menebak dengan benar satu angka; tetapi, Anda TIDAK AKAN diberi tahu apabila angka yang anda tebak hanya salah letaknya.
Sebagai contoh, berikut ini adalah hasil tebakan dari bilangan rahasia 5-angka,
90342 ;2 benar
70794 ;0 benar
39458 ;2 benar
34109 ;1 benar
51545 ;2 benar
12531 ;1 benar
Sedangkan bilangan rahasia yang benar adalah 39542.
Bedasarkan tebakan berikut,
5616185650518293 ;2 benar
3847439647293047 ;1 benar
5855462940810587 ;3 benar
9742855507068353 ;3 benar
4296849643607543 ;3 benar
3174248439465858 ;1 benar
4513559094146117 ;2 benar
7890971548908067 ;3 benar
8157356344118483 ;1 benar
2615250744386899 ;2 benar
8690095851526254 ;3 benar
6375711915077050 ;1 benar
6913859173121360 ;1 benar
6442889055042768 ;2 benar
2321386104303845 ;0 benar
2326509471271448 ;2 benar
5251583379644322 ;2 benar
1748270476758276 ;3 benar
4895722652190306 ;1 benar
3041631117224635 ;3 benar
1841236454324589 ;3 benar
2659862637316867 ;2 benar
Carilah bilangan rahasia dengan panjang 16-angka ini.
Answer: 70f84864f21c4bf07ee53436580cd4bb
Soal 186
Ini adalah catatan dari sistem jaringan telepon dengan satu juta pengguna:
| RecNr | Penelepon | Penerima |
| 1 | 200007 | 100053 |
| 2 | 600183 | 500439 |
| 3 | 600863 | 701497 |
| ... | ... | ... |
Nomor telepon dari penelepon (caller) dan penerima (called) ke-n adalah Caller(n) = S2n-1 dan Called(n) = S2n dimana S1,2,3,... dibuat dengan metode "Lagged Fibonacci Generator":
Untuk 1 ≤ k ≤ 55, Sk = [100003 - 200003k + 300007k3] (modulo 1000000)
Untuk 56 ≤ k, Sk = [Sk-24 + Sk-55] (modulo 1000000)
Jika Caller(n) = Called(n), maka penelepon dianggap salah sambung, dan proses telepon tersebut dianggap gagal; sebaliknya, jika nomor penelepon dan penerima tidak sama, proses telepon dianggap sukses.
Dari awal catatan, kita dapat mengatakan bahwa semua pasangan pengguna telepon X dan Y adalah saling berteman apabila X menelepon Y atau sebaliknya. Hal yang sama, X adalah teman dari Z jika X merupakan teman dari Y, dan Y merupakan teman dari Z; dan begitu seterusnya terbentuk rantai yang lebih panjang.
Nomor telepon perdana menteri adalah 524287. Setelah beberapa telepon yang berhasil tersambung, telepon yang salah sambung tidak dihitung, apakah 99% dari pengguna telepon (termasuk sang perdana menteri) akan menjadi teman, atau temannya teman, dan seterusnya..., dari sang perdana menteri?
Answer: b21d68f1871abf1d5bbcf1206b3f1643
Soal 187
Bilangan komposit adalah bilangan yang memiliki setidaknya dua faktor prima. Sebagai contoh, 15 = 3 × 5; 9 = 3 × 3; 12 = 2 × 2 × 3.
Terdapat sepuluh bilangan komposit kurang dari tiga puluh yang mempunyai persis dua buah faktor prima yang boleh sama ataupun berbeda: 4, 6, 9, 10, 14, 15, 21, 22, 25, 26.
Berapa banyak bilangan komposit n < 108, yang mempunyai persis dua buah faktor prima yang boleh sama ataupun berbeda?
Answer: b3e6977523511d2cbbef8fccb1e394db
Soal 188
Hasil hyperexponentiation atau tetration bilangan a dengan bilangan bulat positif b, dilambangkan dengan a↑↑b atau ba, dan dapat dihitung secara rekursif dengan:
a↑↑1 = a,
a↑↑(k+1) = a(a↑↑k).
Sebagai contoh, 3↑↑2 = 33 = 27, sehingga 3↑↑3 = 327 = 7625597484987 dan 3↑↑4 dihitung secara kasar adalah 103.6383346400240996*10^12.
Carilah delapan angka terakhir dari 1777↑↑1855.
Answer: 62746b4d40a2b87c3dd6caee5d33e6a1
Soal 189
Perhatikan susunan 64 buah segitiga berikut:

Kita akan mewarnai setiap segitiga dengan salah satu dari tiga warna: merah, hijau, atau biru, sehingga tidak ada dua buah segitiga bersebelahan yang mempunyai warna yang sama. Jika berhasil, maka hasil pewarnaan tersebut akan dianggap berhasil. Di soal ini, dua segitiga dikatakan bersebelahan apabila memiliki satu sisi yang sama.
Catatan: Jika hanya sama titik sudutnya saja, segitiga tersebut tidak dianggap bersebelahan.
Contoh berikut ini adalah hasil pewarnaan yang sah pada segitiga di atas:

Proses pewarnaan C' yang didapatkan dari hasil rotasi atau refelksi pewarnaan C akan dianggap berbeda dari C, keduali hasil pewarnaan keduanya identik.
Berapakah banyaknya cara berbeda untuk mewarnai segitiga-segitiga di atas secara sah?
Answer: d3dfdd37601678212b746c34699f1484
Soal 190
Misalkan Sm = (x1, x2, ... , xm) adalah kumpulan m-buah bilangan real positif yang memenuhi x1 + x2 + ... + xm = m, dan memiliki nilai Pm = x1 * x22 * ... * xmm sebesar mungkin.
Sebagai contoh, dapat dibuktikan bahwa [P10] = 4112 ([ ] melambangkan bagian fungsi yang berupa bilangan bulat).
Carilah Σ[Pm] untuk 2 ≤ m ≤ 15.
Answer: 40cfcabd9b30d79ec81151fc756e9946
Soal 191
Sebuah sekolah menawarkan hadiah uang tunai kepada anak yang memiliki tingkat kehadiran dan ketepatan waktu yang baik. Jika mereka absen selama tiga hari berturut-turut, atau terlambat lebih dari satu kali, maka mereka akan kehilangan hadiah mereka.
Selama n-hari, sebuah tulisan tiga huruf dibentuk untuk setiap anak yang akan mempunyai arti L (late/terlambat), O (on time/tepat waktu), dan A (absen).
Terdapat delapan puluh satu macam kehadiran berbeda untuk kegiatan belajar mengajar selama 4 hari yang dapat dibentuk, dan empat puluh tiga di antaranya akan mengarahkan anak kepada hadiah:
OOOO OOOA OOOL OOAO OOAA OOAL OOLO OOLA OAOO OAOA
OAOL OAAO OAAL OALO OALA OLOO OLOA OLAO OLAA AOOO
AOOA AOOL AOAO AOAA AOAL AOLO AOLA AAOO AAOA AAOL
AALO AALA ALOO ALOA ALAO ALAA LOOO LOOA LOAO LOAA
LAOO LAOA LAAO
Berapa banyak kombinasi tulisan seperti di atas yang ada, yang akan mengarahkan anak untuk mendapatkan hadiah, namun untuk kegiatan belajar mengajar yang dilaksanakan selama 30-hari?
Answer: e04dfa598b22a87570f63063f3ff595d
Soal 192
Misalkan x adalah bilangan real.
Sebuah pendekatan terbaik untuk mencari x untuk batas penyebut d, adalah sebuah bilangan rasional r/s dalam bentuk paling sederhana, dengan s ≤ d, sehingga semua bilangan rasional yang lebih dekat kepada x dibanding r/s akan memiliki penyebut lebih besar daripada d:
Sebagai contoh, pendekatan terbaik √13 untuk batas penyebut 20 adalah 18/5, dan pendekatan terbaik √13 untuk batas penyebut 30 adalah 101/28.
Carilah jumlah semua penyebut yang merupakan pendekatan terbaik untuk √n, untuk batas penyebut 1012, dimana n adalah bilangan yang bukan merupakan kuadrat sempurna, dan 1 < n ≤ 100000.
Answer: e5ec7d4b094709b1fcebbd73b10e6264
Soal 193
Sebuah bilangan bulat positif n disebut sebagai bilangan squarefree, jika tidak ada bilangan prima kuadrat yang dapat habis membagi n, sehingga 1, 2, 3, 5, 6, 7, 10, 11 semuanya adalah bilangan squarefree, tapi tidak dengan 4, 8, 9, 12.
Berapa banyak bilangan squarefree yang kurang dari 250?
Answer: ea29fcf755b560777b0b6d8714234d18
Soal 194
Terdapat gambar yang dibuat dengan unit A:  dan unit B:
dan unit B:  , dimana setiap unit ditempelkan satu sama lain pada garis vertikalnya seperti pada gambar:
, dimana setiap unit ditempelkan satu sama lain pada garis vertikalnya seperti pada gambar:

Sebuah susunan dengan tipe (a,b,c) adalah gambar yang dibuat dengan a buah unit A dan b buah unit B, dimana titik-titik pada setiap gambar diwarnai menggunakan c buah warna, sehingga tidak ada dua titik bersebelahan yang mempunyai warna yang sama.
Gambar gabungan di atas merupakan salah satu contoh dari konfigurasi tipe (2,2,6), pada kenyataannya terdapat tipe (2,2,c) untuk c ≥ 4.
N(a,b,c) adalah banyaknya konfigurasi tipe (a,b,c) yang bisa dibentuk.
Sebagai contoh, N(1,0,3) = 24, N(0,2,4) = 92928 dan N(2,2,3) = 20736.
Carilah 8 angka terakhir dari N(25,75,1984).
Answer: e070561d568a80a0e45d7835e3817ba4
Soal 195
Terdapat suatu segitiga dengan panjang sisi yang merupakan bilangan bulat, dan persis satu buah sudut bernilai 60 derajat, segitiga ini akan kita sebut sebagai segitiga 60-derajat.
Misalkan r adalah panjang jari-jari lingkaran dalam suatu segitiga 60-derajat.
Terdapat 1234 buah segitiga 60-derajat yang r ≤ 100.
Sedangkan T(n) adalah banyaknya segitiga 60-derajat dimana r ≤ n, sehingga
T(100) = 1234, T(1000) = 22767, dan T(10000) = 359912.
Carilah T(1053779).
Answer: 0fe232937a6d9f2a40825b86f568a38c
Soal 196
Kita akan membuat sebuah segitigad dari bilangan bulat positif dengan aturan sebagai berikut:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45
46 47 48 49 50 51 52 53 54 55
56 57 58 59 60 61 62 63 64 65 66
. . .
Setiap bilangan pada segitiga tersebut bisa memiliki bilangan yang bersebelahan sampai delapan buah.
Sebuah himpunan tiga bilangan prima akan disebut triplet prime apabila salah satu dari ketiga bilangan prima tersebut bersebelahan dengan kedua bilangan prima lainnya pada segitiga di atas.
Sebagai contoh, pada baris kedua, bilangan prima 2 dan 3 adalah bagian dari suatu triplet prima.
Jika kita memperhatikan baris 8, baris ini berisi dua bilangan prima yang merupakan bagian dari suatu triplet prima lain, yaitu 29 dan 31.
Jika kita memperhatikan baris 9, terdapat hanya satu buah prima yang akan menjadi anggota triplet prima: 37.
Diketahui S(n) adalah jumlah semua bilangan prima yang merupakan anggota triplet prima pada baris ke-n.
Maka S(8)=60 dan S(9)=37.
Diketahui S(10000)=950007619.
Carilah S(5678027) + S(7208785).
Answer: fb6b6b0a4b7b31ba429152bc0b6bd037
Soal 197
Diberikan sebuah fungsi f(x) = ⌊230.403243784-x2⌋ × 10-9 ( ⌊ ⌋ adalah lambang yang berarti bilangan akan dibulatkan ke bawah),
barisan un dibentuk dengan u0 = -1 dan un+1 = f(un).
Carilah un + un+1 untuk n = 1012.
Berikan jawaban anda sampai 9 angka di belakang koma.
Answer: c98cbf87636906f2465d481be815e454
Soal 198
Cara pendekatan terbaik untuk suatu bilangan real x untuk batas penyebut d adalah bilangan rasional r/s (dalam bentuk paling sederhana) dengan s ≤ d, sehingga semua bilangan rasional p/q yang lebih dekat ke x daripada ke r/s akan mempunyai q > d.
Biasanya, cara pendekatan terbaik untuk suatu bilangan real ditentukan oleh besarnya batasan penyebut. Tetapi, terdapat beberapa pengecualian, seperti 9/40, yang mempunyai dua hasil pendekatan terbaik 1/4 dan 1/5 untuk batas penyebut 6. Kita akan menyebut semua bilangan real x sebagai bilangan yang ambigu, apabila terdapat dua hasil pendekatan terbaik x untuk setidaknya satu batas penyebut. Jelas bahwa bilangan ambigu harus merupakan bilangan rasional.
Berapakah banyaknya cara bilangan ambigu x = p/q, 0 < x < 1/100, yang penyebut qnya tidak melebihi 108?
Answer: e59816f440fec9368c681314a127f3ee
Soal 199
Tiga lingkaran dengan jari-jari sama diletakan dalam suatu lingkaran besar, sehingga setiap lingkaran akan saling menyinggung satu sama lain, dan lingkaran yang ada di dalam tidak saling menumpuk satu sama lain. terdapat empat daerah yang masih belum ditutupi, yang akan di isi lagi secara berulang-ulang dengan lingkaran yang juga saling menyinggung lingkaran lainnya.

Pada setiap iterasi, lubang akan di isi dengan sebuah lingkaran sebesar mungkin, dimana setelah lingkaran tersebut diletakkan, akan muncul lubang baru lagi untuk iterasi selanjutnya. Setelah 3 iterasi (seperti pada gambar), terdapat sebanyak 108 lubang dan perbandingan luas lubang dengan luas keseluruhan adalah 0.06790342, dibulatkan sampai delapan angka di belakang koma.
Berapakah perbandingan luas lubang dengan luas keseluruhan setelah 10 kali iterasi?
Berikan jawaban anda yang telah dibulatkan hingga delapan angka di belakang koma, dengan menggunakan format x.xxxxxxxx .
Answer: 0f8fd87159c28ae5fea6ac91a95d48dd
Soal 200
Sqube adalah sebuah bilangan dengan bentuk, p2q3, dimana p dan q adalah bilangan prima berbeda.
Sebagai contoh, 200 = 5223 atau 120072949 = 232613.
Lima bilangan sqube pertama adalah 72, 108, 200, 392, dan 500.
Menariknya, 200 juga merupakan bilangan pertama yang tidak bisa kita buat menjadi bilangan prima apabila salah satu angkanya diganti; bilangan seperti ini akan kita sebut bilangan kebal-prima. Bilangan kebal-prima selanjutnya yang juga merupakan bilangan sqube, dan memiliki angka "200" di dalamnya adalah 1992008.
XCarilah bilangan ke-200 yang kebal-prima, yang juga merupakan bilangan sqube, yang berisi angka "200" di dalamnya.
Answer: c911c8e346aa813da5f5ed4f8e9128d8
Soal 201
Untuk setiap himpunan berisi A buah bilangan, sum(A) adalah hasil penjumlahan dari elemen-elemen A.
Misalkan terdapat himpunan B = {1,3,6,8,10,11}.
Terdapat 20 himpunan bagian yang memiliki tiga anggota, dan jumlah mereka adalah:
sum({1,3,6}) = 10,
sum({1,3,8}) = 12,
sum({1,3,10}) = 14,
sum({1,3,11}) = 15,
sum({1,6,8}) = 15,
sum({1,6,10}) = 17,
sum({1,6,11}) = 18,
sum({1,8,10}) = 19,
sum({1,8,11}) = 20,
sum({1,10,11}) = 22,
sum({3,6,8}) = 17,
sum({3,6,10}) = 19,
sum({3,6,11}) = 20,
sum({3,8,10}) = 21,
sum({3,8,11}) = 22,
sum({3,10,11}) = 24,
sum({6,8,10}) = 24,
sum({6,8,11}) = 25,
sum({6,10,11}) = 27,
sum({8,10,11}) = 29.
Beberapa himpunan bagian menghasilkan jumlah yang sama, dan beberapa menghasilkan hasil yang unik.
Untuk himpunan A, U(A,k) adalah himpunan dari hasil penjumlahan unik untuk k-buah anggota himpunan bagian A, pada contoh kami di atas, kami menemukan U(B,3) = {10,12,14,18,21,25,27,29} dan sum(U(B,3)) = 156.
Sekarang misalkan terdapat himpunan S dengan 100-buah anggota S = {12, 22, ... , 1002}.
S mempunyai 100891344545564193334812497256 himpunan bagian dengan 50-buah anggota.
Tentukan hasil penjumlahan semua bilangan bulat, pada himpunan bagian dari S yang memiliki 50-buah anggota, atau dapat ditulis sum(U(S,50)).
Answer: b7ad07c58c81a940b8ff067a13b2760d
Soal 202
Tiga cermin disusun untuk membentuk sebuah segitiga sama sisi, dengan sisi yang memantulkan cahanyanya diletakkan di sebelah dalam. Terdapat tak hingga buah celah kecil pada setiap titik sudut segitiga, yang memungkinkan sinar laser untuk masuk.
Jika titik sudut diberi label A, B dan C. Terdapat 2 cara untuk sinar laser dapat memasuki titik C, memantul di dalam 11 kali, kemudian keluar ke titik y ang sama: salah satu caranya ditunjukkan pada gambar berikut; cara satunya lagi adalah kebalikan dari cara ini.

Terdapat 80840 cara untuk sinar laser dapat memasuki titik C, memantul 1000001 kali, kemudian keluar melalui titik yang sama.
Dengan berapa cara sinar laser dapat masuk melalui titik C, memantul 12017639147 kali, kemudian keluar melalui titik yang sama?
Answer: e9774949b5efad0d40d60ede379c5321
Soal 203
Koefisien binomial nCk dapat disusun dalam bentuk segitiga, dan hasilnya sama dengan segitiga Pascal, seperti ini:
| 1 | ||||||||||||||
| 1 | 1 | |||||||||||||
| 1 | 2 | 1 | ||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||
Dapat terlihat bahwa delapan baris pertama pada segitiga Pascal berisi dua belas buah angka berbeda: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 dan 35.
Sebuah bilangan bulat positif n disebut sebagai bilangan squarefree, jika tidak ada bilangan prima kuadrat yang dapat membagi habis n. Dari kedua belas bilangan berbeda pada delapan baris pertama segitiga Pascal, semua bilangan kecuali 4 dan 20 adalah bilangan squarefree. Jumlah dari semua bilangan squarefree berbeda pada delapan baris pertama adalah 105.
Carilah jumlah semua bilangan squarefree berbeda pada 51 baris pertama segitiga Pascal.
Answer: d7ec16d216c923d3c927f46cfc914e92
Soal 204
Bilangan Hamming adalah sebuah bilangan positif, yang faktor primanya tidak ada yang lebih besar dari 5.
Sehingga, beberapa bilangan Hamming pertama adalah 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
Terdapat 1105 bilangan Hamming yang tidak melebihi 108.
Kita akan menyebut suatu bilangan positif sebagai bilangan Hamming tergeneralisasi dengan tipe n, apabila bilangan tersebut tidak mempunyai faktor prima lebih besar dari n.
Sehingga, bilangan Hamming biasa sebenarnya adalah merupakan bilangan Hamming tergeneralisasi dengan tipe 5.
Berapa banyak bilangan Hamming tergeneralisasi dengan tipe 100, yang tidak melebihi 109?
Answer: 4118ffb9edc56a033b5b27ca0bf34366
Soal 205
Peter mempunyai sembilan buah dadu bersisi empat (berbentuk piramidal), setiap sisi dadu diberi angka 1, 2, 3, 4.
Colin mempunyai enam buah dadu bersisi enam (berbentuk kubus), setiap sisi dadu diberi angka 1, 2, 3, 4, 5, 6.
Peter dan Colin memutar dadu mereka, dan membandingkan hasil penjumlahannya: yang memiliki jumlah lebih besar akan menang. Hasil akan dianggap seri apabila hasil penjumlahan dari keduanya sama.
Berapakah peluang dadu piramidal milik Peter mengalahkan dadu kubus milik Colin? Berikan jawaban Anda sampai tujuh angka di belakang koma dengan format 0.abcdefg
Answer: ba6c6c3888227a0799eca38191b587be
Soal 206
Carilah bilangan bulat positif unik, yang kuadratnya memiliki bentuk 12_3_4_5_6_7_8_9_0,
dimana setiap tanda “” merupakan sebuah angka.
Answer: 09f9d87cb4b1ebb34e1f607e55a351d8
Soal 207
Untuk beberapa bilangan bulat positif k, terdapat sebuah partisi bilangan bulat dengan bentuk 4t = 2t + k,
dimana 4t, 2t, dan k semuanya merupakan bilangan bulat positif, dan t adalah bilangan real.
Contoh dua partisi pertama adalah 41 = 21 + 2 dan 41.5849625... = 21.5849625... + 6.
Partisi dimana t nya juga merupakan bilangan bulat disebut sempurna.
Untuk setiap m ≥ 1, P(m) adalah peluang suatu partisi adalah sempurna, dengan k ≤ m.
Sehingga P(6) = 1/2.
Pada tabel berikut ini akan didaftarkan beberapa kemungkinan untuk P(m)
P(5) = 1/1
P(10) = 1/2
P(15) = 2/3
P(20) = 1/2
P(25) = 1/2
P(30) = 2/5
...
P(180) = 1/4
P(185) = 3/13
Carilah nilai m terkecil, dimana P(m) < 1/12345
Answer: 3f17b264ed1717fe5fbde1e399bd501f
Soal 208
Sebuah robot bergerak dengan jalur satu per lima busur lingkaran (72°), dengan bebas memilih arah putaran, apakah searah jarum jam atau berlawanan jarum jam pada setiap langkahnya, namun tidak boleh berputar saat diam di tempat.
Salah satu dari 70932 jalur tertutup yang dibentuk dari 25 busur dimulai dari utara adalah

Diketahui bahwa robot mula-mula menghadap utara, berapa banyak jalur tertutup yang dapat dibuat, dengan 70 buah busur (70 kali berjalan), sehingga setelah langkah terakhir robot, robot tersebut akan kembali ke titik awalnya?
(Setiap busur dan titik mulai boleh dilewati berkali-kali.)
Answer: 3010e33173f30e0aac79e84835b48823
Soal 209
Sebuah tabel kebenaran biner dengan k-buah input, didapatkan dengan memetakan k-buah input biner (angka biner, 0 [salah] atau 1 [benar]) menjadi 1 buah output biner. Sebagai contoh, tabel kebenaran biner dengan 2-buah input, untuk operasi logika AND dan XOR adalah:
| x | y | x AND y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| x | y | x XOR y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Berapa banyak hasil dari tabel kebenaran biner dengan 6-buah input τ, yang memenuhi
Untuk semua 6-buah input biner (a, b, c, d, e, f)?
Answer: 954157aa4762df2ee29580ee5a351b13
Soal 210
Terdapat himpunan S(r) berisi titik (x,y) dengan koordinat yang berupa bilangan bulat yang memenuhi |x| + |y| ≤ r.
Misalkan titk O memiliki koordinat (0,0) dan titik C memiliki koordinat (r/4,r/4).
Misalkan N(r) adalah banyaknya titik B pada S(r), sehingga segitiga OBC memiliki sudut tumpul, yaitu sudut α yang memenuhi 90° < α < 180°
Sebagai contoh, N(4)=24 dan N(8)=100.
Berapakah N(1,000,000,000)?
Answer: 0c808b02789c4db462322ab2ac070bbb
Soal 211
Untuk bilangan bulat positif n, σ2(n) adalah hasil penjumlahan dari kuadrat pembagi habisnya. Sebagai contoh,
Carilah hasil penjumlahan untuk semua n, 0 < n < 64,000,000 yang σ2(n) adalah kuadrat sempurna.
Answer: 5fe0ed146690e7bca448687a94353a73
Soal 212
Sebuah kubus sejajar sumbu, memiliki parameter { (x0,y0,z0), (dx,dy,dz) }, untuk semua titik (X,Y,Z) yang memenuhi x0 ≤ X ≤ x0+dx, y0 ≤ Y ≤ y0+dy dan z0 ≤ Z ≤ z0+dz. Volume dari kubus bisa didapat dengan hasil perkalian, dx × dy × dz. Sedangkan volume gabungan dari sekumpulan kubus didapat dengan cara menggabungkan semua kubus, dan dapat bernilai lebih kecil dibandingkan dengan jika kita menghitung volume kubus satu per satu, karena bisa saja terdapat kubus yang saling tumpang tindih (overlap).
Misalkan C1,...,C50000 adalah kumpulan 50000 buah kubus yang sejajar sumbu, sehingga Cn mempunyai parameter
x0 = S6n-5 modulo 10000
y0 = S6n-4 modulo 10000
z0 = S6n-3 modulo 10000
dx = 1 + (S6n-2 modulo 399)
dy = 1 + (S6n-1 modulo 399)
dz = 1 + (S6n modulo 399)
dimana S1,...,S300000 muncul dari "Lagged Fibonacci Generator":
Untuk 1 ≤ k ≤ 55, Sk = [100003 - 200003k + 300007k3] (modulo 1000000)
Untuk 56 ≤ k, Sk = [Sk-24 + Sk-55] (modulo 1000000)
Sehingga, C1 memiliki parameter {(7,53,183),(94,369,56)}, C2 memiliki parameter {(2383,3563,5079),(42,212,344)}, dan seterusnya.
Volume gabungan dari 100 kubus pertama, C1,...,C100, adalah 723581599.
Berapakah volume gabungan dari semua 50000 buah kubus tersebut, C1,...,C50000 ?
Answer: 76650c9c077929e1ce5a80a1ac81fa96
Soal 213
Sebuah kotak-kotak berukuran 30×30 berisi 900 kutu, pada mulanya, satu kutu di tiap kotak.
Saat lonceng berbunyi, setiap kutu akan melompat ke kotak di sebelahnya secara acak (biasanya terdapat 4 kemungkinan arah, kecuali untuk kutu yang ada di pojok kotak-kotak).
Berapakah nilai harapan banyaknya kotak yang kosong setelah lonceng dibunyikan 50 kali? Berikan jawaban Anda yang telah dibulatkan hingga enam angka di belakang koma.
Answer: f81ee7dd444a3d895a4a446f9d115bf8
Soal 214
Misalkan φ adalah fungsi Totient Euler, sehingga untuk bilangan asli n, φ(n) adalah banyaknya bilangan k, 1 ≤ k ≤ n, dimana FPB(k,n) = 1.
Dengan mengulang-ulang fungsi φ, semua bilangan bulat positif akan berkurang terus menerus hingga mencapai 1.
Sebagai contoh, jika kita memulai fungsi dengan bilangan 5, maka rantai 5,4,2,1 akan terbentuk.
Berikut ini adalah daftar dari semua rantai dengan panjang 4:
7,6,2,1
8,4,2,1
9,6,2,1
10,4,2,1
12,4,2,1
14,6,2,1
18,6,2,1
Hanya dua dari rantai-rantai tersebut yang dimulai oleh bilangan prima, hasil penjumlahan kedua bilangan prima tersebut adalah 12.
Berapakah hasil penjumlahan semua bilangan prima kurang dari 40000000, yang akan menghasilkan rantai seperti di atas dengan panjang 25?
Answer: 1cefd865483c03552d5247ffb05685c7
Soal 215
Kita akan mengamati masalah membangun dinding, jika disediakan batu bata berukuran 2×1 dan 3×1 (Ukuran horizontal×vertikal), untuk kekuatan ekstra, celah antara dua baris batu bata tidak pernah membentuk garis lurus, atau dapat juga disebut tidak pernah terbentuk "running crack".
Sebagai contoh, tembok berukuran 9×3 berikut ini tidak diperbolehkan, karena adanya garis lurus (running crack) yang ditunjukkan dengan garis merah:

Terdapat delapan cara untuk membangun dinding berukuran 9×3 yang bebas garis lurus (running crack), dan dapat dituliskan W(9,3) = 8.
Hitunglah W(32,10).
Answer: 60212c9ec4a6cd1d14277c32b6adf2d8
Soal 216
Terdapat bilangan t(n) dengan bentuk t(n) = 2n2-1 dengan n > 1.
Beberapa bilangan pertama dari bentuk di atas adalah 7, 17, 31, 49, 71, 97, 127 dan 161.
Ditemukan bahwa hanya 49 = 7*7 dan 161 = 7*23 yang bukan merupakan bilangan prima.
Untuk n ≤ 10000 terdapat sebanyak 2202 bilangan t(n) yang merupakan bilangan prima.
Berapakah banyaknya bilangan t(n) yang prima, untuk n ≤ 50,000,000 ?
Answer: e512153424a482deb9de401ac0465a72
Soal 217
Sebuah bilangan bulat positif dengan k-angka, disebut seimbang apabila hasil penjumlahan ⌈k/2⌉-angka pertama sama dengan hasil penjumlahan ⌈k/2⌉-angka terakhir, dimana ⌈x⌉, adalah hasil pembulatan ke atas dari x, sehingga ⌈π⌉ = 4 dan ⌈5⌉ = 5.
Sebagai contoh, semua bilangan palindrom adalah bilangan seimbang, contoh lainnya adalah 13722.
T(n) adalah jumlah semua bilangan seimbang yang kurang dari 10n.
Sehingga: T(1) = 45, T(2) = 540 dan T(5) = 334795890.
Carilah T(47) mod 315
Answer: 11bff97aac06892e1a07ebf7febfa8db
Soal 218
Misalkan terdapat segitiga siku-siku dengan panjang sisi a=7, b=24 dan c=25.
Luas segitiga ini adalah 84, yang habis dibagi dengan bilangan sempurna 6 dan 28.
Selanjutnya, segitiga ini adalah segitiga siku-siku primitif, karena FPB(a,b)=1 dan FPB(b,c)=1.
Serta c merupakan bilangan kuadrat sempurna.
Kita akan menyebut suatu segitiga siku-siku sempurna apabila
-segitiga tersebut adalah segitiga siku-siku primitif
-hipotenusanya adalah bilangan kuadrat sempurna
Kita akan menyebut sebuah segitiga siku-siku sangat sempurna apabila
-segitiga tersebut merupakan segitiga sempurna, dan
-luasnya kelipatan bilangan sempurna 6 dan 28.
Berapa banyak segitiga siku-siku yang bukan merupakan segitiga siku-siku sangat sempurna, dengan c≤1016?
Answer: cfcd208495d565ef66e7dff9f98764da
Soal 219
A dan B merupakan string biner (hanya berisi angka 0 dan 1).
Jika A sama dengan bagian paling kiri sepanjang length(A) bit dari B, maka A dapat disebut sebagai prefix dari B.
Sebagai contoh, 00110 adalah prefix dari 001101001, tapi bukan prefix dari 00111 atau 100110.
Sebuah kode bebas prefix dengan ukuran n adalah kumpulan n buah string biner berbeda, sehingga tidak ada string yang merupakan prefix string lainnya. Sebagai contoh, ini adalah sebuah kode bebas prefix dengan ukuran 6:
0000, 0001, 001, 01, 10, 11
Sekarang misalkan kita perlu membayar satu penny untuk mengirimkan sebuah bit '0', namun perlu empat penny untuk mengirimkan sebuah bit '1'.
Maka total biaya yang diperlukan pada kode bebas prefix di atas adalah 35 penny, yang merupakan kemungkinan biaya paling murah untuk pertanyaan ini.
Secara singkat, kita akan menulis biaya dengan cara Cost(6) = 35.
Berapakah Cost(109) ?
Answer: 578c22ef288b88c60fbcf4541351aff5
Soal 220
D0 adalah string berisi dua karakter "Fa". Sedangkan untuk n≥1, kita harus menurunkan Dn dari Dn-1 dengan aturan penulisan string:
"a" → "aRbFR"
"b" → "LFaLb"
Sehingga, D0 = "Fa", D1 = "FaRbFR", D2 = "FaRbFRRLFaLbFR", dan seterusnya.
String tersebut dapat di artikan sebagai suatu perintah pada aplikasi pembuat gambar di komputer, dengan "F" berarti "gambar garis ke depan satu satuan", "L" berarti "berputar ke kiri 90 derajat", "R" berarti "berputar ke kanan 90 derajat", dan "a" serta "b" diabaikan. Posisi awal kursor komputer adalah (0,0), dan menghadap ke atas, ke arah (0,1).
Lalu Dn akan membentuk suatu gambar menarik yang dikenal sebagai Heighway Dragon dengan orde n. Sebagai contoh, D10 ditunjukan pada gambar berikut; dengan menghitung setiap huruf "F" sebagai satu langkah, titik (18,16) yang di tandai tersebut bisa dicapai setelah berjalan 500 langkah.

Dimanakan posisi kursor setelah 1012 langkah di D50 ?
Berikan jawaban Anda dengan format x,y tanpa spasi.
Answer: e2018d8efde8ea00319f1adc042f150b
Soal 221
Kita akan menyebut sebuah bilangan bulat positif A sebagai "bilangan bulat Alexandrian", apabila terdapat bilangan bulat p, q, r yang memenuhi:
| A = p · q · r dan |
|
= |
|
+ |
|
+ |
|
Sebagai contoh, 630 adalah sebuah bilangan bulat Alexandrian (p = 5, q = −7, r = −18). Kenyataannya, 630 adalah bilangan bulat Alexandrian ke-6, 6 bilangan bulat Alexandrian pertama adalah: 6, 42, 120, 156, 420 and 630.
Carilah bilangan bulat Alexandrian ke-150000.
Answer: cb000c24f653d9c8f78b74123e6515ab
Soal 222
Berapakah panjang pipa terpendek, yang memiliki jari-jari dalam 50mm, yang bisa menampung 21 buah bola dengan jari-jari 30mm, 31mm, ..., 50mm?
Berikan jawaban anda dalam satuan mikrometer (10-6 m) dibulatkan ke bilangan bulat terdekat.
Answer: 6984ba429b968467619ec98a8ee51abf
Soal 223
Terdapat segitiga yang memiliki panjang sisi berupa bilangan bulat, dengan panjang sisi a ≤ b ≤ c, segitiga ini akan disebut segitiga hampir lancip, apabila sisi-sisinya memenuhi
a2 + b2 = c2 + 1.
Berapa banyak segitiga hampir lancip yang memiliki keliling ≤ 25,000,000?
Answer: cb875e59736a1967c8da8fc8062a6bc5
Soal 224
Sebuah segitiga yang mempunyai panjang sisi a ≤ b ≤ c dapat disebut segitiga hampir tumpul, jika sisi-sisinya memenuhi
a2 + b2 = c2 - 1.
Berapa banyak segitiga hampir tumpul yang memiliki keliling ≤ 75,000,000?
Answer: c43cfb12750dee27b4b0d016261e831b
Soal 225
Barisan 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, 653, 1201 ...
dibentuk dengan T1 = T2 = T3 = 1 dan Tn = Tn-1 + Tn-2 + Tn-3.
Dapat terlihat bahwa 27 tidak dapat membagi suku manapun dalam barisan ini.
Bahkan, 27 adalah bilangan ganjil pertama yang memiliki sifat ini.
Carilah bilangan ganjil ke-124, yang tidak dapat membagi suku manapun dalam barisan di atas.
Answer: f1981e4bd8a0d6d8462016d2fc6276b3
Soal 226
Kurva blancmange adalah kumpulan titik (x,y) yang memenuhi 0 ≤ x ≤ 1 dan  ,
,
dimana s(x) = adalah selisih antara x dengan bilangan bulat terdekat.
Luas di bawah kurva blancmange sama dengan ½, yang ditunjukkan dengan warna pink pada diagram berikut.

Misalkan C adalah sebuah lingkaran dengan pusat (¼,½) dan jari-jari ¼, yang ditunjukkan dengan warna hitam pada diagram di atas.
Berapakah luas daerah di bawah kurva blancmange, yang dibatasi oleh C?
Berikan jawaban Anda yang telah dibulatkan menjadi delapan angka di belakang koma, dengan format 0.abcdefgh
Answer: ce6fd32d1d2fb58c4c0c1f7962c39f04
Soal 227
“The Chase” adalah sebuah permainan yang menggunakan dua buah dadu, dan dimainkan oleh pemain yang berjumlah genap.
Para pemain duduk di sekitar sebuah meja; permainan dimulai dengan dua pemain yang saling bersebrangan masing-masing memegang sebuah dadu. Pada setiap giliran, kedua pemain akan melempar dadu tersebut.
Jika pemain berhasil mengeluarkan angka 1, ia harus memberikan dadu ke orang di sebelah kirinya; jika ia mberhasil mengeluarkan angka 6, ia haurs memberikan dadu ke orang di sebelah kananya; selain itu, ia harus tetap memegang dadu sampai giliran selanjutnya.
Permainan berakhir saat ada satu pemain yang memiliki dua buah dadu, setelah dadu dilempar dan diserahkan satu sama lain; pemain tersebut kemudian dianggap kalah.
Jika permainan dimainkan oleh 100 orang, berapakah perkiraan banyaknya giliran yang terjadi hingga permainan berakhir??
Berikan jawaban anda yang dibulatkan sebesar sepuluh angka.
Answer: 7b87cd0a96f0f2f12f911cdc66608d95
Soal 228
Sn adalah bangun berjumlah sisi n yang memiliki titik sudut vk (k = 1,2,…,n) have coordinates:
| xk = cos( 2k-1/n ×180° ) | |
| yk = sin( 2k-1/n ×180° ) |
Setiap Sn akan dianggap memiliki bagian sebelah dalam keliling yang terisi penuh.
Hasil penjumlahan Minkowski S+T, dari dua buah bangun S dan T bisa didapat dengan cara menjumlahkan setiap titik di S kepada setiap titik di T, sesuai dengan koordinat masing-masing: (u, v) + (x, y) = (u+x, v+y).
Sebagai contoh, hasil penjumlahan dari S3 dan S4 adalah bangun dengan enam sisi bewarna pink berikut:

Berapakah banyaknya sisi yang dimiliki oleh S1864 + S1865 + … + S1909?
Answer: 35d0195ddaf58e52e12400de1c9333d8
Soal 229
Perhatikan bilangan 3600. Bilangan ini sangat istimewa, karena
3600 = 202 + 2×402
3600 = 302 + 3×302
3600 = 452 + 7×152
Dengan cara yang sama, kita dapat menebukan bahwa 88201 = 992 + 2802 = 2872 + 2×542 = 2832 + 3×522 = 1972 + 7×842.
Pada tahun 1747, Euler membuktikan bahwa terdapat bilangan yang dapat direpresentasikan dengan penjumlahan dua bilangan kuadrat. Kita akan memperhatikan bilangan n yang bisa memenuhi keempat tipe representasi berikut ini:
n = a22 + 2 b22
n = a32 + 3 b32
n = a72 + 7 b72,
dimana ak dan bk adalah bilangan bulat positif.
Terdapat 75373 buah bilangan seperti di atas yang tidak melebihi 107.
Berapa banyak bilangan yang kurang dari 2×109?
Answer: d68b5ec8df4a56991901f67afbdef24f
Soal 230
Untuk dua buah string berisi angka-angka A dan B, kita akan menyatakan FA,B sebagai barisan (A,B,AB,BAB,ABBAB,...), setiap suku didapat dengan cara menggabungkan dua buah suku sebelumnya.
lebih jauh lagi, kita nyatakan DA,B(n) sebagai angka ke-n pada suku pertama dari FA,B yang memiliki setidaknya n buah angka.
Contoh:
Misalkan A=1415926535, B=8979323846. Kita akan mencari DA,B(35).
Beberapa suku pertama dari FA,B adalah:
1415926535
8979323846
14159265358979323846
897932384614159265358979323846
14159265358979323846897932384614159265358979323846
Maka DA,B(35) adalah angka ke-35 pada suku ke lima, yaitu 9.
Sekarang kita akan mengganti A dengan 100 buah angka di belakang koma dari π:
14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
dan B diganti dengan 100 buah angka setelahnya lagi:
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196 .
Carilah ∑n = 0,1,...,17 10n× DA,B((127+19n)×7n) .
Answer: 040735038021ff4704bbd3a0964369ef
Soal 231
Koefisien binomial 10C3 = 120.
120 = 23 × 3 × 5 = 2 × 2 × 2 × 3 × 5, dan 2 + 2 + 2 + 3 + 5 = 14.
Sehingga, hasil penjumlahan dari faktor-faktor prima 10C3 adalah 14.
Carilah hasil penjumlahan dari faktor-faktor prima 20000000C15000000.
Answer: ef8bc4d9a843e71126bd10b5065132a5
Soal 232
Dua pemain akan menggunakan sebuah koin yang sama, dan menggunakannya secara bergantian untuk bermain "balapan". Pada giliran permain pertama, ia melempar koin sekali: jika muncul gambar kepala, ia mendapatkan satu nilai; jika muncul gambar ekor, ia tidak mendapatkan nilai. Pada giliran pemain kedua, ia harus terlebih dahulu memilih sebuah bilangan bulat positif T, dan kemudian melempar koin sebanyak T kali: Jika pada semua lemparan muncul gambar kepala, ia mendapatkan nilai 2T-1; selain itu, ia tidak mendaptkan nilai. Pemain pertama memulai giliran pertama kali. Pemenangnya adalah pemain yang terlebih dahulu mencapai nilai 100 atau lebih.
Pada setiap giliran pemain kedua akan selalu memilih bilangan T, yang membuatnya mempunyai peluang sebesar mungkin untuk menang.
Berapakah peluang pemain 2 menang?
Berikan jawaban Anda dengan dibulatkan sampai delapan angka di belakang koma, dengan format 0.abcdefgh .
Answer: c8d5b243aa6e6b507725766f7c197a1d
Soal 233
f(N) adalah banyaknya titik pada lingkaran yang koordinatnya adalah bilangan bulat, di lingkaran yang melalui (0,0), (N,0),(0,N), dan (N,N).
Dapat dibuktikan bahwa\ f(10000) = 36.
Berapakah hasil penjumlahan semua bilangan bulat positif N ≤ 1011 sehingga f(N) = 420 ?
Answer: 7e80b27798170abb493e3b4671bd82ca
Soal 234
Untuk bilangan bulat n ≥ 4, kita akan menyebut akar kuadrat prima bawah dari n, yang dilambangkan dengan lps(n), sebagai bilangan prima terbesar ≤ √n, dan akan menyebut akar kuadrat prima atas dari n, dengan lambang ups(n), sebagai bilangan prima terkecil ≥ √n.
Sebagai contoh, lps(4) = 2 = ups(4), lps(1000) = 31, ups(1000) = 37.
Kita akan menyebut bilangan bulat n ≥ 4 semidivisible, jika salah satu dari lps(n) dan ups(n) dapat membagi habis n, tetapi tidak keduanya.
Hasil penjumlahan dari bilangan semidivisible yang kurang dari 15 adalah 30, bilangan semidivisible lainnya adalah 8, 10 dan 12.
15 tidak disebut semidivisible karena ia merupakan kelipatan lps(15) = 3 dan ups(15) = 5.
Contoh lebih lanjut, hasil penjumlahan dari 92 bilangan semidivisible kurang dari 1000 adalah 34825.
Berapakah hasil penjumlahan semua bilangan semidivisible yang kurang dari 999966663333 ?
Answer: c24a5d60f8ce5d04dec7466987c84d68
Soal 235
Diberikan barisan aritmatik-geometrik u(k) = (900-3k)rk-1.
s(n) = Σk=1...nu(k).
Carilah nilai dari r yang memenuhi s(5000) = -600,000,000,000.
Berikan jawaban Anda dibulatkan 12 angka di belakang koma.
Answer: 41b13508789be1001308e065d4f83ea2
Soal 236
Supplier 'A' dan 'B' menyediakan sejumlah barang untuk keranjang parsel mewah:
| Produk | 'A' | 'B' |
|---|---|---|
| Beluga Caviar | 5248 | 640 |
| Christmas Cake | 1312 | 1888 |
| Gammon Joint | 2624 | 3776 |
| Vintage Port | 5760 | 3776 |
| Champagne Truffles | 3936 | 5664 |
Namun, para supplier mencoba sekuat tenaga untuk mengirimkan barang mereka dengan kondisi sempurna, tetapi selalu terdapat kerusakan yang terlihat.
Para supplier membandingkan performa mereka menggunakan dua cara statistik:
- Cara rata-rata kerusakan per lima produk, yaitu setiap supplier menghitung banyaknya barang rusak, lalu membagi dengan jumlah barang yang dikirimkan, untuk setiap lima buah barang yang masuk.
- Cara rata-rata kerusakan keseluruhan, yaitu setiap supplier menghitung banyaknya barang yang rusak dengan banyaknya barang yang dikirimkan oleh supplier tersebut, untuk keseluruhan barang.
Mengejutkannya, para supplier menemukan, bahwa semua hasil metode rata-rata kerusakan per lima produk lebih buruk (besar) untuk 'B' dibandingkan untuk 'A' dengan perbandingan nilai rata-rata m>1; namun jika menggunakan metode rata-rata kerusakan keseluruhan, perbandingan rata-ratanya akan bernilai lebih buruk untuk 'A' dibandingkan dengan 'B', juga dengan nilai perbandingan m.
Terdapat tiga puluh lima m>1 dimana kejadian mengejutkan seperti ini terjadi, kejadian dengan nilai perbandingan paling kecil adalah 1476/1475.
Berapakah kemungkinan terbesar dari m?
Berikan jawaban ada dalam pecahan yang paling sederhana, dengan format u/v.
Answer: 6e707fcffc510520d981ae16a29579bb
Soal 237
T(n) adalah banyaknya jalur pada papan permainan berukuran 4 × n yang memiliki aturan:
- Jalur harus dimulai dari pojok kiri atas.
- Jalur dapat dibuat dengan gerakan ke atas, bawah, kiri, atau kanan sebanyak satu kotak.
- Jalur harus melewati setiap kotak persis satu kali.
- Jalur harus berakhir di pojok kiri bawah.
Diagram berikut ini menunjukkan salah satu jalur dari papan berukuran 4 × 10:

T(10) adalah 2329. Berapakah T(1012) modulo 108?
Answer: 0742988a3948491b15fb48e476c78a6a
Soal 238
Create a sequence of numbers using the “Blum Blum Shub” pseudo-random number generator:
s[0] = 14025256
s[n+1] = s[n]^2 mod 20300713
Concatenate these numbers s[0]s[1]s[2]… to create a string w of infinite length. Then, w = 14025256741014958470038053646…
For a positive integer k, if no substring of w exists with a sum of digits equal to k, p(k) is defined to be zero. If at least one substring of w exists with a sum of digits equal to k, we define p(k) = z, where z is the starting position of the earliest such substring.
For instance:
The substrings 1, 14, 1402, … with respective sums of digits equal to 1, 5, 7, … start at position 1, hence p(1) = p(5) = p(7) = … = 1.
The substrings 4, 402, 4025, … with respective sums of digits equal to 4, 6, 11, … start at position 2, hence p(4) = p(6) = p(11) = … = 2.
The substrings 02, 0252, … with respective sums of digits equal to 2, 9, … start at position 3, hence p(2) = p(9) = … = 3.
Note that substring 025 starting at position 3, has a sum of digits equal to 7, but there was an earlier substring (starting at position 1) with a sum of digits equal to 7, so p(7) = 1, not 3.
We can verify that, for 0 < k ≤ 10^3, ∑ p(k) = 4742.
Find ∑ p(k), for 0 < k ≤ 2·10^15.
Answer: 424ed6613a372ccb9a90dddb8961ca16
Soal 239
Satu set disk diberi nomor dari 1 hingga 100, dan diletakkan pada suatu barisan dengan urutan acak.
Berapakah peluang kita menemukan persis 22 buah disk dengan bilangan prima berpindah tempat dari posisi aslinya?
(Disk dengan bilangan non-prima berapapun boleh ditemukan baik pada tempat aslinya, atau bukan.)
Berikan jawaban Anda yang dibulatkan 12 angka di belakang koma dengan format 0.abcdefghijkl.
Answer: 451fd2b8c19fbfec650a5c4699f6ef6e
Soal 240
Terdapat 1111 cara untuk membuat lima buah dadu ber sisi 6 (sisinya diberi angka 1 sampai 6), untuk dapat diputar sehingga tiga dadu dengan nilai terbesar berjumlah 15. Beberapa contohnya adalah:
D1,D2,D3,D4,D5 = 4,3,6,3,5
D1,D2,D3,D4,D5 = 4,3,3,5,6
D1,D2,D3,D4,D5 = 3,3,3,6,6
D1,D2,D3,D4,D5 = 6,6,3,3,3
Berapa banyak cara untuk dua puluh buah dadu ber sisi 12 (sisinya diberi angka 1 sampai 12), dapat diputar untuk menghasilkan hasil penjumlahan sepuluh angka terbesar sama dengan 70?
Answer: cb31a3106db3876e77cd160664cd683e
Soal 241
Untuk bilangan bulat positif n, σ(n) adalah jumlah semua pembagi habis dari n, sehingga σ(6) = 1 + 2 + 3 + 6 = 12.
Bilangan sempurna, seperti yang mungkin sudah Anda ketahui, adalah bilangan dengan σ(n) = 2n.
| Kita akan menyatakan hasil bagi sempurna dari suatu bilangan bulat positif sebagai | p(n) | = | σ(n) n |
. |
Carilah hasil penjumlahan semua bilangan bulat positif n ≤ 1018, dimana p(n) memiliki bentuk k + 1⁄2, dan dimana k adalah bilangan bulat.
Answer: 556bfef2cacd1eff8af9126c5c13dcbc
Soal 242
Diberikan himpunan {1,2,...,n}, kita nyatakan f(n,k) adalah banyaknya himpunan bagian dengan k-anggota, yang hasil penjumlahan anggota-anggotanya adalah bilangan ganjil. Sebagai contoh, f(5,3) = 4, semenjak himpunan {1,2,3,4,5} memiliki empat buah himpunan bagian dengan 3 anggota, dan yang memiliki hasil penjumlahan ganjil adalah: {1,2,4}, {1,3,5}, {2,3,4} and {2,4,5}.
Saat nilai n, k dan f(n,k) ketiga-tiganya adalah ganjil, dapat kita katakan bahwa mereka membuat
sebuah triplet ganjil [n,k,f(n,k)].
Terdapat persis lima triplet ganjil dengan n ≤ 10, yaitu:
[1,1,f(1,1) = 1], [5,1,f(5,1) = 3], [5,5,f(5,5) = 1], [9,1,f(9,1) = 5] dan [9,9,f(9,9) = 1].
Berapakah banyaknya triplet ganjil dengan n ≤ 1012 ?
Answer: ba73cb75365ddca8f94a23e3fedfb6de
Soal 243
Sebuah pecahan positif yang pembilangnya kurang dari penyebutnya akan kita sebut sebagai pecahan layak.
Untuk setiap penyebut d, akan selalu ada d−1 buah pecahan layak; sebagai contoh, dengan d = 12:
1/12 , 2/12 , 3/12 , 4/12 , 5/12 , 6/12 , 7/12 , 8/12 , 9/12 , 10/12 , 11/12 .
Kita akan menyebut pecahan yang tidak dapat disederhanakan lagi sebagai pecahan paling sederhana.
Lebih lanjut lagi, kita akan menyatakan ketahanan dari suatu penyebut, R(d), sebagai rasio dari pecahan paling sederhana dengan pecahan layak; sebagai contoh, R(12) = 4/11 .
Kenyataannya, d = 12 adalah penyebut terkecil yang memiliki nilai ketahanan R(d) < 4/10 .
Carilah bilangan penyebut d terkecil, yang memiliki nilai ketahanan R(d) < 15499/94744 .
Answer: 531721a10786c5c2a444b474fcf039f9
Soal 244
Anda mungkin telah mengetahui permainan Fifteen Puzzle. Disini, bukan menggunakan kotak bernomor, kita akan menggunakan tujuh kotak merah dan delapan kotak biru.
Sebuah gerakan dilambangkan dengan huruf kapital dari arah yang di inginkan (Left/Kiri, Right/Kanan, Up/Atas, Down/Bawah), yang akan melambangkan arah kotak bergeser untuk mengisi kotak kosong, sebagai contoh, dimulai dari konfigurasi (S), dengan urutan LULUR kita akan mencapai konfigurasi (E):
| (S) |  | , (E) |  |
Untuk setiap jalan, nilai checksum dapat dihitung dengan:
checksum = (checksum × 243 + m1) mod 100 000 007
checksum = (checksum × 243 + m2) mod 100 000 007
…
checksum = (checksum × 243 + mn) mod 100 000 007
| L | 76 |
| R | 82 |
| U | 85 |
| D | 68 |
Untuk urutan LULUR di atas, nilai chekcsum yang ada adalah 19761398.
Sekarang, dimulai dengan konfigurasi (S), carilah semua jalur terpendek untuk mencapai konfigurasi (T).
| (S) |  | , (T) |  |
Berapakah hasil penjumlahan dari semua checksums untuk jalur yang memiliki jarak terpendek?
Answer: f8fd502ec1d0084a79d43d9dc5bd3a3d
Soal 245
Kita akan menyebut pecahan yang sudah tidak bisa disederhanakan lagi sebagai pecahan resilient.
Lebih lanjut lagi, kita akan menyatakan nilai resilience dari suatu penyebut dengan R(d), sebagai perbandingan dari semua pecahan kurang dari 1 dengan penyebut d yang sudah tidak bisa disederhanakan lagi, dengan banyaknya pecahan yang ada; sebagai contoh, R(12) = 4⁄11.
| Maka, nilai resilience dari bilangan d > 1 adalah | φ(d) d − 1 |
, dimana φ adalah fungsi totient Euler. |
| Kemudian, kita akan menyatakan coresilience dari n > 1 sebagai C(n) | = | n − φ(n) n − 1 | . |
| Nilai coresilience dari bilangan prima p adalah C(p) | = | 1 p − 1 | . |
Carilah hasil penjumlahan dari semua bilangan bulat komposit 1 < n ≤ 2×1011, dimana C(n) adalah pecahan dengan pembilang 1.
Answer: 0ebeb502fb0bd7157609835d27c266bc
Soal 246
Definisi dari elips adalah:
Diberikan lingkaran c dengan pusat M dan jari-jari r dan sebuah titik G yang memenuhi d(G,M)<r, lokus dari semua titik yang sama panjangnya dari c dan G akan membentuk elips.
Pembentukkan titik-titik pada elips ditunjukkan pada gambar berikut. </p>

Diketahui terdapat titik M(-2000,1500) dan G(8000,1500).
Diketahui juga bahwa lingkaran c memiliki pusat M dan berjari-jari 15000.
Lokus dari titik-titik yang memiliki panjang yang sama dari G dan c akan membentuk elips e.
Dari titik P di luar e, digambar dua buah garis singgung elips t1 dan t2.
Titik dimana t1 dan t2 menyentuh elips adalah R dan S.

Berapa banyak titik potong P memiliki sudut RPS lebih besar dari 45 derajat?
Answer: 94c521ffeb906391d161b66fec433827
Soal 247
Perhatikan daerah yang dibatasi oleh 1 ≤ x dan 0 ≤ y ≤ 1/x.
S1 adalah persegi terbesar yang bisa muat di bawah kurva.
S2 adalah persegi terbesar yang bisa muat diletakkan di daerah sisanya, dan seterusnya.
indeks dari Sn berupa pasangan bilangan (kiri, bawah), menandakan banyaknya persegi di sebelah kiri dari Sn dan banyaknya persegi di bawah Sn.

Diagram di atas menunjukkan beberapa persegi sesuai dengan aturan di atas, yang diberi nomor.
Pada S2 terdapat satu persegi di sebelah kirinya, dan tidak ada persegi di bawahnya, sehingga indeks dari S2 adalah (1,0).
Dapat terlihat bahwa indeks dari persegi S32 adalah (1,1), dan sama seperti indeks dari persegi S50.
50 adalah nilai n terbesar yang indeks dari persegi Sn bernilai (1,1).
Berapakah nilai n terbesar, yang memiliki indeks persegi Sn bernilai (3,3)?
Answer: 257956694e7665e3d512ad5b819ef79d
Soal 248
Bilangan n pertama yang menghasilkan φ(n)=13! adalah 6227180929.
Carilah bilangan ke-150,000 yang juga seperti itu.
Answer: b69a3ba674f6c7c5f2ce244f9e9cc873
Soal 249
S = {2, 3, 5, ..., 4999} adalah himpunan bilangan prima kurang dari 5000.
Carilah banyaknya himpunan bagian dari S, yang hasil penjumlahan dari elemen-elemennya adalah bilangan prima.
Masukkan 16 angka terakhir dari jawaban Anda.
Answer: a470ee3ca52f2b68d7034e48b39b8b26
Soal 250
Carilah banyaknya himpunan bagian tidak kosong dari {11, 22, 33,..., 250250250250}, yang hasil penjumlahan elemen-elemennya habis dibagi 250. Masukkan 16 angka terakhir dari jawaban Anda.
Answer: 4a5614f3700956273fe0d271f921d5f4
Soal 251
Sebuah triplet bilangan bulat positif (a,b,c) akan disebut triplet Cardano apabila memenuhi kondisi:

Sebagai contoh, (2,1,5) adalah triplet Cardano.
Terdapat 149 triplet Cardano dimana a+b+c ≤ 1000.
Carilah berapa banyak triplet Cardano yang ada, dimana a+b+c ≤ 110,000,000.
Answer: 9690315a09a4d9f58dcc19ad96e6e889
Soal 252
Diberikan himpunan titik-titk pada suatu bidang, kita akan menyatakan lubang konveks sebagai poligon konveks yang dibentuk dari titik apapun, dan tidak berisi titik lain di sebelah dalamnya (titik masih boleh berada di keliling poligon).
Sebagai contoh, gambar di bawah ini menunjukkan himpunan dari dua puluh buah titik, dan beberapa lubang konveks seperti yang dijelaskan di atas. Lubang konveks ditunjukkan oleh segi tujuh berwarna merah memiliki luas 1049694.5 satuan luas, dimana luas ini adalah luas terbesar yang memungkinkan dibentuk oleh lubang konveks pada titik-titik yang diberikan.

Pada contoh di atas, 20 titik pertama (T2k−1, T2k), untuk k = 1,2,…,20, dicari dengan alat pembuat bilangan acak:
| S0 | = | 290797 |
| Sn+1 | = | Sn2 mod 50515093 |
| Tn | = | ( Sn mod 2000 ) − 1000 |
sehingga didapat (527, 144), (−488, 732), (−454, −947), …
Berapakah luas lubang konveks terbesar, pada kumpulan 500 titik pertama yang dibentuk dengan alat pembuat bilangan acak di atas?
Jawab hingga ketelitian satu angka di belakang koma.
Answer: 53b1ced82e1b588d756750c4d2f77e0d
Soal 253
Seorang anak kecil memiliki “ulat nomor” yang berisi empat puluh buah jigsaw puzzle, setiap potong puzzle memiliki sebuah nomor padanya, sehingga, saat semua puzzle digabung dalam satu garis, akan muncul nomor 1 sampai 40 secara berurutan.
Setiap malam, ayah dari anak tersebut harus mengambil potongan puzzle ulat yang telah tersebar di ruang bermain. Ia mengambil potongan puzzle secara acak, lalu meletakannya di urutan yang benar.
Maka lama kelamaan ulat akan terbentuk, akan terbentuk segmen ulat berbeda yang lama kelamaan akan tersambung menjadi satu ulat utuh.
Banyaknya segmen ulat dimulai dari nol buah (tidak ada segmen tercipta sama sekali), hingga terdapat sebelas atau dua belas buah segmen ulat, lalu kembali menjadi nol lagi sebelum semua segmen bergabung menjadi satu (semua potongan telah diletakkan dengan benar).
For example:
| Banyak Potongan Puzzle | Banyak Segmen Tercipta Sejauh ini |
| 12 | 1 |
| 4 | 2 |
| 29 | 3 |
| 6 | 4 |
| 34 | 5 |
| 5 | 4 |
| 35 | 4 |
| … | … |
M adalah banyak maksimal dari segmen ulat yang bisa terbentuk pada saat puzzle ulat dirapikan secara acak.
Untuk ulat dengan sepuluh potong puzzle, besarnya kemungkinan untuk setipa M adalah
| M | Kemungkinan |
| 1 | 512 |
| 2 | 250912 |
| 3 | 1815264 |
| 4 | 1418112 |
| 5 | 144000 |
sehingga nilai M yang paling sering muncul adalah 3 dan rata-ratanya adalah 385643⁄113400 = 3.400732, dibulatkan hingga enam angka di belakang koma.
nilai M yang paling sering muncul untuk puzzle ulat dengan empat puluh potong puzzle adalah 11; namun berapakah nilai rata-rata dari M?
Berikan jawaban Anda dibulatkan hingga enam angka di belakang koma.
Answer: 228de0a37019fd7c7051029f3d126422
Soal 254
Dinyatakan f(n) adalah hasil penjumlahan dari faktorial angka-angka n. Sebagai contoh, f(342) = 3! + 4! + 2! = 32.
Dinyatakan sf(n) adalah hasil penjumlahan dari angka-angka pada f(n). Sehingga sf(342) = 3 + 2 = 5.
Dinyatakan g(i) adalah bilangan bulat positif n terkecil, yang memenuhi sf(n) = i. Sehingga walaupun sf(342) adalah 5, sf(25) juga 5, jadi dapat disimpulkan bahwa g(5) adalah 25.
Dinyatakan sg(i) sebagai hasil penjumlahan angka-angka pada g(i). Sehingga sg(5) = 2 + 5 = 7.
Lebih lanjut, dapat dibuktikan bahwa g(20) adalah 267 dan ∑ sg(i) untuk 1 ≤ i ≤ 20 adalah 156.
Berapakah ∑ sg(i) untuk 1 ≤ i ≤ 150?
Answer: 936014adf2de65d41979ad900325e485
Soal 255
Kita akan menyatakan suatu akar-kuadrat-dibulatkan sebuah bilangan bulat positif n, sebagai akar kuadrat dari n yang dibulatkan ke bilangan bulat terdekat.
Prosedur berikut ini (didasari dari metode Heron yang diadaptasikan dengan aritmatika bilangan bulat) akan menemukan akar-kuadrat-dibulatkan dari n:
d adalah banyaknya angka (digit) dari bilangan n.
Jika d bernilai ganjil, tetapkan x0 = 2×10(d-1)⁄2.
Jika d bernilai genap, tetapkan x0 = 7×10(d-2)⁄2.
Ulangi:

sampai xk+1 = xk.
Sebagai contoh, kita akan mencari akar-kuadrat-dibulatkan dari n = 4321.
n mempunyai 4 angka (digit), sehingga x0 = 7×10(4-2)⁄2 = 70.

Karena x2 = x1, maka kita berhenti sampai di sini.
Sehingga, setelah dua kali pengulangan (iterasi), kita telah menemukan akar-kuadrat-dibulatkan dari 4321 adalah 66 (akar kuadrat aslinya adalah 65.7343137…).
Banyaknya pengulangan (iterasi) yang diperlukan saat menggunakan metode ini cukup rendah.
Sebagai contoh, kita dapat mencari akar-kuadrat-dibulatkan dari bilangan bulat 5 angka (digit) (10,000 ≤ n ≤ 99,999) dengan rata-rata 3.2102888889 kali pengulangan (rata-rata tersebut telah dibulatkan 10 angka di belakang koma).
Dengan menggunakan prosedur seperti di atas, berapakah rata-rata banyaknya pengulangan (iterasi) yang diperlukan untuk mencari akar-kuadrat-dibulatkan dari bilangan 14 angka (digit) (1013 ≤ n < 1014)?
Berikan jawaban Anda dibulatkan 10 angka di belakang koma.
Catatan: Lambang ⌊x⌋ dan ⌈x⌉ memiliki arti masing-masing dibulatkan ke bawah dan dibulatkan ke atas.
Answer: 12be028b156b49faa1137febda940ab5
Soal 256
Tatami adalah tikar berbentuk persegi panjang, yang digunakan untuk menutup seluruh lantai suatu ruangan, tanpa ada yang saling tumpang tindih satu sama lain.
Diasumsikan bahwa hanya terdapat satu macam tatami dengan ukuran 1×2, maka akan terdapat beberapa batasan dari bentuk dan ukuran ruang yang lantainya bisa ditutupi.
Untuk masalah ini, kita menganggap hanya ada ruangan berbentuk persegi panjang dengan ukuran berupa bilangan bulat a, b dan luas s genap, s = a·b.
Kita menggunakan istilah 'luas' untuk menyatakan luas permukaan lantai ruangan, dan — tanpa menghilangkan segala kemungkinan yang ada — kita akan menambahkan kondisi a ≤ b.
Terdapat satu aturan untuk menyusun tatami: tidak boleh ada titik yang menjadi tempat bertemu ujung empat tikar berbeda.
Sebagai contoh, perhatikan dua susunan berikut ini untuk ruangan berukuran 4×4:

Susunan di sebelah kiri dapat diterima, sedangkan yang di sebelah kanan tidak: tanda "X" bewarna merah di tengah-tengah, menandakan tempat dimana empat tatami bertemu.
Karena aturan ini, beberapa ukuran dengan luas genap tertentu tidak bisa ditutupi oleh tatami: kita akan sebut mereka ruangan tanpa tatami.
Lebih lanjut, kita nyatakan T(s) sebagai banyaknya ruangan tanpa tatami dengan luas s.
Ruangan tanpa tatami terkecil memiliki luas s = 70 dan berdimensi 7×10.
Tetapi terdapat ruangan lain dengan luas s = 70 yang bisa ditutup oleh tatami; mereka adalah: 1×70, 2×35 dan 5×14.
Sehingga, T(70) = 1.
Dengan cara yang sama, kita dapat buktikan bahwa T(1320) = 5, karena terdapat persis 5 buah ruangan tanpa tatami yang memiliki luas s = 1320:
20×66, 22×60, 24×55, 30×44 and 33×40.
Kenyataanya, s = 1320 adalah ukuran luas s terkecil dimana T(s) = 5.
Carilah luas ruangan s terkecil, dimana T(s) = 200.
</span>
Answer: ef8eb0c177d00a5b80e1723786a22698
Soal 257
Diberikan sebuah segitiga ABC dengan sisi-sisi bilangan bulat a ≤ b ≤ c.
(AB = c, BC = a and AC = b).
Garis bagi dari segitiga tersebut berpotongan pada titik E, F, dan G (perhatikan gambar berikut).

Segmen garis EF, EG dan FG membagi segitiga ABC menjadi empat segitiga kecil: AEG, BFE, CGF dan EFG.
Dapat dibuktikan bahwa pada keempat segitiga tersebut, perbandingan luas(ABC)/luas(segitiga keicl) adalah merupakan bilangan rasional.
Dan, terdapat beberapa segitiga yang memimiliki sebagian atau semua nilai perbandingan berupa bilangan bulat.
Berapakah banyaknya segitiga ABC dengan panjang keliling≤100,000,000 yang memiliki nilai perbandingan luas(ABC)/luas(AEG) berupa bilangan bulat?
</span>
Answer: 3ba58bde91c83c98904050d90e466ce2
Soal 258
Sebuah barisan dinyatakan dengan:
- gk = 1, for 0 ≤ k ≤ 1999
- gk = gk-2000 + gk-1999, untuk k ≥ 2000.
Carilah gk mod 20092010 untuk k = 1018.
Answer: 18eca0138f3acbde20dcc24ed06627ea
Soal 259
Sebuah bilangan bulat positif dikatakan dapat dicapai apabila bilangan tersebut dapat dibentuk dari operasi aritmatika yang memenuhi aturan berikut:
- Menggunakan angka (digit) 1 sampai 9, sesuai urutannya, dan masing-masing angka (digit) digunakan sekali.
- Setiap angka (digit) yang bersebelahan dapat digabung (sebagai contoh, menggunakan angka (digit) 2, 3 dan 4 kita bisa mendapatkan bilangan 234).
- Hanya terdapat empat macam operasi aritmatika yang boleh digunakan (penjumlahan, pengurangan, perkalian dan pembagian).
- Setiap operasi aritmatika dapat bebas digunakan berkali-kali, atau bahkan tidak digunakan sama sekali.
- Tanda negatif di depan bilangan tidak diperbolehkan.
- Diperbolehkan untuk menggunakan tanda kurung sebanyak-banyaknya untuk menentukan urutan operasi.
Sebagai contoh, 42 adalah bilangan yang dapat dicapai, karena (1/23) * ((4*5)-6) * (78-9) = 42.
Berapakah hasil penjumlahan semua bilangan bulat positif yang dapat dicapai?
Answer: 771828a57c269d873335c9091af78f76
Soal 260
Sebuah permainan dimainkan dengan tiga tumpuk batu dan dua pemain.
Saat gilirannya, seorang pemain mengambil satu atau lebih batu dari tumpukan. Tetapi, apabila ia mengambil batu di lebih dari satu tumpukan, ia harus mengambil jumlah batu dengan banyak yang sama pada setiap tumpukan.
Dengan kata lain, pemain memilih N>0 dan mengambil:
- N buah batu dari salah satu tumpukan; atau
- masing-masing N buah batu dari dua buah tumpukan (total 2N); atau
- masing-masing N buah batu dari tiga buah tumpukan (total 3N).
Sebuah susunan kemenangan adalah cara menyusun batu untuk membuat pemain pertama menjadi menang.
Sebagai contoh, (0,0,13), (0,11,11) dan (5,5,5) adalah susunan kemenangan, karena pemain pertama dapat dengan segera mengambil semua batu yang ada.
Sebuah susunan kekalahan adalah cara menyusun batu untuk membuat pemain kedua menjadi pemenang, tidak peduli apapun yang dilakukan oleh pemain pertama.
Sebagai contoh, (0,1,2) dan (1,3,3) adalah susunan kekalahan: setiap langkah yang sah akan meninggalkan susunan kemenangan untuk pemain kedua.
Misalkan susunan kekalahan dinyatakan dengan (xi,yi,zi) dimana xi ≤ yi ≤ zi ≤ 100.
Dapat dibuktikan bahwa Σ(xi+yi+zi) = 173895.
Carilah Σ(xi+yi+zi) dimana (xi,yi,zi) adalah susunan kekalahan yang memenuhi
with xi ≤ yi ≤ zi ≤ 1000.
Answer: cab69719e6968409ba167707a09875cb
Soal 261
Kita akan menyebut bilangan bulat positif k sebagai poros-kuadrat, jika terdapat sepasang bilangan bulat m > 0 dan n ≥ k, sehingga hasil penjumlahan dari (m+1) buah bilangan kuadrat berurutan sampai k sama dengan hasil penjumlahan dari m buah bilangan kuadrat berurutan dari (n+1):
Beberapa contoh poros-kuadrat kecil adalah
- 4: 32 + 42 = 52
- 21: 202 + 212 = 292
- 24: 212 + 222 + 232 + 242 = 252 + 262 + 272
- 110: 1082 + 1092 + 1102 = 1332 + 1342
Carilah hasil penjumlahan dari semua poros-kuadrat berbeda ≤ 1010.
Answer: d45ddf64010ed143228a6a6b84837de9
Soal 262
Fungsi berikut ini akan menggambarkan topografi dari daerah kontinu suatu pegunungan, nilai ketinggian h di titik (x,y) manapun adalah:

Seekor nyamuk akan terbang dari A(200,200) ke B(1400,1400), tanpa keluar dari daerah yang dibatasi 0 ≤ x, y ≤ 1600.
Karena adanya halangan pada daerah pegunungan, nyamuk tersebut akan terbang ke atas pada titik A dengan ketinggian f. Lalu, dengan ketinggian f yang konstan, nyamuk tersebut akan terbang lurus melewati semua rintangan sampai tiba di titik B, persis di atas titik B.
Pertama-tama, tentukan fmin, yaitu ketinggian minimum yang memungkinkan nyamuk melakukan perjalanan dari A ke B, pada batas yang telah ditentukan.
Lalu, carilah jarak terpendek antara A dan B yang bisa didapat dengan cara terbang pada ketinggian konstan fmin.
Jarak terpendek tersebut adalah jawaban Anda, bulatkan hingga tiga angka di belakang koma.
<font "size=2">Catatan: Untuk memudahkan, fungsi ketinggian di atas diketik ulang di bawah, namun dalam bentuk yang cocok untuk sebagian besar bahasa pemrograman:
h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) ) * exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )</font>
Answer: a5921e175a44d31e7f82f7f9a61a36af
Soal 263
Perhatikan bilangan 6. Faktor dari 6 adalah: 1,2,3 dan 6.
Setiap bilangan dimulai dari 1 sampai 6 (termasuk 6 itu sendiri) dapat ditulis sebagai hasil penjumlahan faktor berbeda dari:
1=1, 2=2, 3=1+2, 4=1+3, 5=2+3, 6=6.
Sebuah bilangan n disebut sebagai bilangan praktis apabila setiap bilangan dimulai dari 1 sampai n (termasuk n) dapat dinyatakan sebagai hasil penjumlahan faktor-faktor berbeda dari n.
Sepasang bilangan prima berurutan dengan beda enam disebut pasangan seksi (karena kata "sex" adalah bahasa Latin untuk "enam"). Pasangan seksi pertama adalah (23, 29).
Kita mungkin dapat menemukan pasangan seksi rangkap tiga, yang berarti terdapat tiga pasangan seksi berurutan, sehingga anggota ke dua dari setiap pasangan adalah anggota pertama dari pasangan selanjutnya.
Kita akan menyebut bilangan n yang :
- (n-9, n-3), (n-3,n+3), (n+3, n+9) membentuk pasangan seksi rangkap tiga, dan
- bilangan n-8, n-4, n, n+4 dan n+8 adalah bilangan praktis,
Carilah hasil penjumlahan empat buah bilangan surga insinyur pertama.
Answer: 8fe3eb7196c69a080740e076cff9b4a1
Soal 264
Diasumsikan semua segitiga memiliki sifat:
- Semua titik sudutnya berada pada koordinat dengan bilangan bulat.
- Pusat dari lingkaran luar segitiganya berada di titik origin (0,0).
- Titik potong ketiga buah garis tinggi pada segitiga berada pada titik H(5, 0).
Terdapat sembilan buah segitiga seperti ini yang memiliki panjang keliling ≤ 50.
Dituliskan dan digambarkan secara berurutan bedasarkan panjang kelilingnya, mereka adalah:
| A(-4, 3), B(5, 0), C(4, -3) A(4, 3), B(5, 0), C(-4, -3) A(-3, 4), B(5, 0), C(3, -4) A(3, 4), B(5, 0), C(-3, -4) A(0, 5), B(5, 0), C(0, -5) A(1, 8), B(8, -1), C(-4, -7) A(8, 1), B(1, -8), C(-4, 7) A(2, 9), B(9, -2), C(-6, -7) A(9, 2), B(2, -9), C(-6, 7) |
 |
Hasil penjumlahan keliling-keliling segitiga tersebut, dibulatkan hingga empat angka di belakang koma adalah 291.0089.
Carilah segitiga seperti di atas dengan panjang keliling ≤ 105.
Lalu sebagai jawaban Anda, masukkan hasil penjumlahan keliling-keliling segitiga tersebut dibulatkan hingga empat angka di belakang koma.
Answer: 287514a045a38be0a75a1786694c77ee
Soal 265
2N angka biner dapat diletakkan pada sebuah lingkaran, sehingga jika N-digit sub-barisan dibaca searah jarum jam semuanya berbeda.
Untuk N=3, memungkinkan dibuat dua susunan melingkar yang memenuhi aturan di atas, hasil rotasi dapat diabaikan:

Untuk lingkaran di sebelah kiri, hasil 3-digit sub-barisan yang ada, dibaca searah jarum jam, adalah:
000, 001, 010, 101, 011, 111, 110 and 100.
Setiap susunan melingkar dapat di terjemahkan menjadi bilangan dengan cara menyatukan semua digit biner, dimulai dari sub-barisan yang semua digitnya nol sebagai bit paling kiri, dan berlanjut searah jarum jam. Dua susunan untuk N=3 dapat diterjemahkan menjadi 23 dan 29:
S(N) adalah hasil penjumlahan dari bilangan-bilangan hasil terjemahan berbeda, kita dapat melihat bahwa S(3) = 23 + 29 = 52.
Carilah S(5).
Answer: c25cebbc8dce4bdcf96cb395a11afcc3
Soal 266
Faktor dari 12 adalah: 1,2,3,4,6 dan 12.
Faktor dari 12 yang tidak melebihi akar kuadrat dari 12 adalah 3.
Kita akan menyebut faktor terbesar dari bilangan bulat n, yang tidak melebihi akar kuadrat n, sebagai akar kuadrat palsu (pseudo square root/PSR) dari n.
Dapat dibuktikan bahwa PSR(3102)=47.
p adalah hasil kali bilangan prima kurang dari 190.
Carilah PSR(p) mod 1016.
Answer: 32da1d501e539ab509f104e2db68d57a
Soal 267
Anda diberikan kesempatan investasi unik.
Dengan modal awal £1, Anda dapat memilih sebanyak f bagian, dari modal Anda untuk dipertaruhkan pada permainan lempar koin berulang-ulang sampai 1000 kali lemparan.
Anda mendapat dua kali lipat dari taruhan Anda jika muncul sisi kepala pada koin, dan Anda harus menyerahkan taruhan Anda jika muncul sisi ekor pada koin.
Sebagai contoh, jika f = 1/4, untuk lemparan koin pertama Anda mempertaruhkan £0.25, dan jika muncul sisi kepala, anda mendapatkan £0.5 sehingga Anda memiliki total £1.5. Lalu Anda kembali mempertaruhkan £0.375 dan jika hasil lemparan kedua Anda adalah ekor, maka sisa uang Anda menjadi £1.125.
Dengan memilih nilai f terbaik, yang dapat memaksimalkan peluang Anda untuk memenangkan setidaknya £1,000,000,000 setelah 1,000 kali lemparan koin, berapakah peluang Anda menjadi seorang miliyarder?
Segala perhitungan diasumsikan eksak (tidak ada pembulatan), namun berikan jawaban Anda dibulatkan 12 angka di belakang koma dengan format 0.abcdefghijkl.
Answer: b8dd3306c2c64eacb0ac36b414892edb
Soal 268
Dapat dibuktikan bahwa terdapat 23 buah bilangan bulat positif kurang dari 1000 yang habis dibagi oleh setidaknya empat buah bilangan prima berbeda kurang dari yang 100.
Carilah berapa banyak bilangan bulat positif kurang dari 1016 yang habis dibagi oleh setidaknya empat buah bilangan prima kurang dari 100.
Answer: 6f84b20c10311cb24a824416a3c3e0a4
Soal 269
Akar dari sebuah polinom P(x) adalah nilai x yang akan membuat polinom memenuhi persamaan P(x) = 0.
Kemudian dinyatakan Pn adalah sebuah polinom, yang koefisien-koefisiennya adalah digit-digit dari n.
Sebagai contoh, P5703(x) = 5x3 + 7x2 + 3.
Dapat kita lihat bahwa:
- Pn(0) adalah digit terakhir dari n,
- Pn(1) adalah hasil penjumlahan semua digit dari n,
- Pn(10) adalah n itu sendiri.
Dinyatakan Z(k) sebagai banyaknya bilangan bulat positif n, yang tidak melebihi k, dimana polinom Pn memiliki setidaknya satu akar bilangan bulat.
Dapat dibuktikan bawha Z(100 000) adalah 14696.
Berapakah Z(1016)?
Answer: f7ba868cb52a9b9c7e58b1b92e230be8
Soal 270
Sebuah kertas berbentuk persegi dengan ukuran N×N, N adalah bilangan bulat, diletakkan dengan salah satu titik sudutnya terletak pada origin (0,0), dan dua titik sudut lainnya diletakkan sepanjang sumbu x dan y. Kemudian, kita potong kertas tersebut dengan mengikuti aturan berikut:
- Kita hanya akan memotong membentuk garis lurus antara dua titik yang ada pada dua sisi berbeda pada persegi, dan kedua titik tersebut mempunyai koordinat bilangan bulat.
- Dua buah hasil potongan tidak boleh saling bertemu, namun ujung dari beberapa potongan boleh bertemu di titik yang sama.
- Lakukan terus hingga tidak terdapat lagi potongan yang bisa dibuat.
Dengan menganggap hasil refleksi atau rotasi sebagai hasil yang berbeda, C(N) adalah banyaknya cara untuk memotong persegi berukuran N×N. Sebagai contoh, C(1) = 2 dan C(2) = 30 (ditunjukkan pada gambar berikut).

Berapakah C(30) mod 108 ?
Answer: 2a592dfd1e9e3e9e38578affa7c72605
Soal 271
Untuk bilangan positif n, dinyatakan S(n) sebagai hasil penjumlahan bilangan bulat x, dimana 1<x<n dan
x3≡1 mod n.
Saat n=91, terdapat 8 kemungkinan nilai untuk x, yaitu : 9, 16, 22, 29, 53, 74, 79, 81.
Sehingga, S(91)=9+16+22+29+53+74+79+81=363.
Carilah S(13082761331670030).
Answer: c4157aab542bd0dfa465c890e1286cc5
Soal 272
Untuk bilangan positif n, dinyatakan C(n) sebagai banyaknya bilangan bulat x, dimana 1<x<n dan
x3≡1 mod n.
Saat n=91, terdapat 8 kemungkinan nilai untuk x, yaitu : 9, 16, 22, 29, 53, 74, 79, 81.
Sehingga, C(91)=8.
Carilah hasil penjumlahan bilangan positif n≤1011 dimana C(n)=242.
Answer: d84d2020055b3e8867dc359e739e0312
Soal 273
Terdapat sebuah persamaan dengan bentuk: a2 + b2 = N, 0 ≤ a ≤ b, a, b dan N adalah bilangan bulat.
Untuk N=65 terdapat dua solusi:
a=1, b=8 dan a=4, b=7.
Kita akan menyebut S(N) sebagai hasil penjumlahan semua nilai a dari semua solusi pada a2 + b2 = N, 0 ≤ a ≤ b, a, b dan N adalah bilangan bulat.
Sehingga S(65) = 1 + 4 = 5.
Carilah ∑S(N), untuk semua bilangan bukan kuadrat N yang hanya habis dibagi oleh bilangan prima dengan bentuk 4k+1, dengan 4k+1 < 150.
Answer: 2b03731e58e9d60e559ee5fdce4f0d14
Soal 274
Untuk setiap bilangan bulat p > 1 yang koprima dengan 10, selalu terdapat bilangan kelipatan faktor positif m < p yang menjaga suatu bilangan tetap habis dibagi oleh p untuk fungsi berikut ini untuk segala bilangan bulat positif, n:
f(n) = (semua kecuali digit terakhir dari n) + (digit terakhir dari n) * m
Sehingga, jika m adalah kelipatan faktor untuk p, maka f(n) habis dibagi oleh p jika dan hanya jika n habis dibagi oleh p.
(Saat n jauh lebih besar dibanding p, f(n) akan kurang dari n dan proses berulang dari f akan menghasilkan bilangan yang habis dibagi p.)
Sebagai contoh, kelipatan faktor untuk 113 adalah 34.
f(76275) = 7627 + 5 * 34 = 7797 : 76275 dan 7797 keduanya habis dibagi 113
f(12345) = 1234 + 5 * 34 = 1404 : 12345 dan 1404 keduanya tidak habis dibagi 113
Hasil penjumlahan kelipatan faktor untuk bilangan prima yang koprima dengan 10 dan kurang dari 1000 adalah 39517. Berapakah hasil penjumlahan dari kelipatan faktor untuk bilangan prima yang koprima dengan 10 dan kurang dari 107?
Answer: ffd68ca67b9c3ea2653d375051e70288
Soal 275
Kita akan menyatakan sebuah patung seimbang dengan orde n sebagai berikut:
- Sebuah polyomino yang dibuat dari n+1 persegi yang dikenal sebagai blok (n persegi)
dan sebuah alas tiang (persegi sisanya); - Alas tiang terletak pada posisi (x = 0, y = 0);
- Blok mempunyai koordinat y yang lebih besar dari nol (sehingga alas tiang harus menjadi satu-satunya persegi di paling bawah);
- Pada sumbu x, pusat massa dari seluruh blok yang digabungkan harus sama dengan nol.
Saat menghitung patung, segala macam susunan yang merupakan refleksi terhadap sumbu y tidak dianggap berbeda. Sebagai contoh, terdapat 18 patung seimbang dengan orde 6 yang ditunjukkan pada gambar di bawah; perlu diingat bahwa setiap pasang patung hasil pencermina (terhadap sumbu y) dihitung sebagai satu patung:

Terdapat 964 patung seimbang dengan orde 10 dan 360505 dengan orde 15.
Berapa banyak patung seimbang yang memiliki orde 18?
Answer: a2a192f9790dcbfe4b450a82c4461d4a
Soal 276
Terdapat segitiga dengan panjang sisi a, b dan c berupa bilangan bulat dengan a ≤ b ≤ c.
Sebuah segitiga dengan sisi bilangan bulat (a,b,c) disebut primitif jika FPB(a,b,c)=1.
Berapa banyak segitiga primitif dengan panjang sisi bilangan bulat yang ada dengan keliling tidak melebihi 10 000 000?
Answer: 29ae64e74ebfdf459dac56786e95c5d5
Soal 277
Sebuah barisan Collatz yang telah dimodifikasi berisi bilangan bulat yang dimulai dari a1 dan didapatkan dengan cara berikut:
an+1 = an/3 jika an habis dibagi 3. Kita akan menyebut ini sebagai langkah turun besar (large downward step), "D".
an+1 = (4an + 2)/3 jika an dibagi 3 menghasilkan sisa 1. Kita akan menyebut ini sebagai langkah naik (upward step), "U".
an+1 = (2an - 1)/3 jika an dibagi 3 menghasilkan sisa 2. Kita akan menyebut ini sebagai langkah turun kecil (small downward step), "d".
Barisan berhenti saat terdapat an = 1.
Diberikan bilangan bulat sembarang, kita dapat mendaftarkan daftar langkah-langkahnya.
Sebagai contoh jika a1=231, maka terbentuk barisan {an}={231,77,51,17,11,7,10,14,9,3,1} yang sesuai dengan langkah "DdDddUUdDD".
Tentu saja, terdapat barisan lain yang dimulai dengan langkah-langkah yang sama "DdDddUUdDD....".
Sebagai contoh, jika a1=1004064, maka langkah-langkahnya DdDddUUdDDDdUDUUUdDdUUDDDUdDD.
Kenyataannya, 1004064 adalah bilangan a1 > 106 terkecil yang dimulai dengan DdDddUUdDD.
Berapakah nilai a1 > 1015 terkecil yang dimulai dengan barisan "UDDDUdddDDUDDddDdDddDDUDDdUUDd"?
Answer: 9508afff135320c18d82c93a8b70cd11
Soal 278
Diketahui terdapat bilangan bulat 1 < a1 < a2 <... < an, maka terdapat kombinasi linear
q1a1 + q2a2 + ... + qnan = b, dengan menggunakan qk ≥ 0 bilangan bulat.
Perlu diingat bahwa untuk sekumpulan ak, tidak semua nilai b bisa digunakan.
Sebagai contoh, jika a1 = 5 dan a2 = 7, tidak ada q1 ≥ 0 dan q2 ≥ 0 yang memiliki nilai b
1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18 atau 23.
Kenyataannya, 23 adalah bilangan bukan b terbesar untuk a1 = 5 dan a2 = 7.
Kita kemudian akan menyebut f(5, 7) = 23.
Dengan cara yang sama, dapat ditunjukkan bahwa f(6, 10, 15)=29 dan f(14, 22, 77) = 195.
Carilah ∑ f(p*q,p*r,q*r), dimana p, q dan r adalah bilangan prima dan p < q < r < 5000.
Answer: 7e680606b5e9890a19894dbdbbbd102a
Soal 279
Berapa banyak segitiga yang memiliki panjang sisi bilangan bulat, dan setidaknya satu buah sudut bilangan bulat (diukur dalam derajat), serta panjang kelilingnya tidak melebihi 108?
Answer: 1f51455a8180fdeeb21285dfb6cba45f
Soal 280
Seekor semut pekerja berjalan secara acak pada kisi berukuran 5x5. Perjalanan dimulai dari kotak paling tengah. Pada setiap langkahnya, semut bergerak ke kotak di sebelahnya secara acak, tetapi tidak keluar dari kisi; sehingga terdapat 2, 3 atau 4 gerakan yang mungkin pada setiap langkah, tergantung dimana semut tersebut berada.
Saat memulai perjalanan, sebuah biji diletakkan pada setiap kotak di barisan paling bawah. Saat semut tidak membawa biji semut akan bergerak ke kotak bagian bawah yang terdapat biji, semut tersebut akan mengambil biji dari kotak. Semut tersebut akan menjatuhkan biji ke kotak kosong pada baris di atasnya yang pertama kali dicapai.
Berapakah banyaknya langkah sampai semua biji dijatuhkan hingga baris paling atas?
Berikan jawaban Anda dibulatkan 6 angka di belakang koma.
Answer: 27f07f04d1908e5ce4fa6eac09881cc2
Soal 281
Anda diberikan sebuah pizza (berbentuk lingkaran sempurna) yang telah dipotong menjadi m·n buah potongan dan Anda ingin memiliki persis satu macam topping pada setiap potongnya.
f(m,n) menyatakan banyaknya cara meletakkan topping pada pizza dengan m macam topping berbeda (m ≥ 2), dengan menggunakan setiap topping persis pada n potong pizza (n ≥ 1).
Hasil Refleksi dianggap berbeda, tetapi rotasi tidak.
Sebagai contoh, f(2,1) = 1, f(2,2) = f(3,1) = 2 dan f(3,2) = 16.
Berbagai pilihan peletakan topping f(3,2) ditunjukkan pada gambar berikut:

Carilah hasil penjumlahan dari semua f(m,n) yang memenuhi f(m,n) ≤ 1015.
Answer: ceee6ced9d64aad844310c8ce2aae2b7
Soal 282
Untuk bilangan bulat tidak negatif m, n, fungsi Ackermann A(m, n) dinyatakan sebagai berikut:

Sebagai contoh A(1, 0) = 2, A(2, 2) = 7 dan A(3, 4) = 125.
Carilah  A(n, n) dan berikan jawaban Anda yang telah di modulo dengan 148.
A(n, n) dan berikan jawaban Anda yang telah di modulo dengan 148.
Answer: a1cc665e127af4e907e13087ee777bd5
Soal 283
Terdapat segitiga dengan panjang sisi 6, 8 dan 10. Dapat dilihat bahwa panjang keliling dan luasnya sama-sama 24. Sehingga perbandingan luas/keliling-nya sama dengan 1.
Terdapat juga segitiga dengan panjang sisi 13, 14 dan 15. Kelilingnya sama dengan 42, sedangkan luasnya sama dengan 84. Sehingga untuk segitiga ini perbandingan luas/keliling-nya sama dengan 2.
Carilah hasil penjumlahan keliling semua segitiga yang bersisi bilangan bulat, dimana segitiga tersebut memiliki perbandingan luas/keliling berupa bilangan bulat positif tidak melebihi 1000.
Answer: 08afda4bc05c8f3ef71c9ffea1ddc0c8
Soal 284
Bilangan 3-digit 376 dalam sistem bilangan desimal adalah salah satu contoh bilangan yang memiliki sifat spesial, yaitu digit akhir dari hasil kuadratnya juga sama dengan angka tersebut: 3762 = 141376. Kita akan menyebut bilangan dengan sifat ini sebagai bilangan kuadrat mantap.
Bilangan kuadrat mantap juga dapat dilihat pada sistem bilangan lain. Pada sistem bilangan basis 14, bilangan 3-digit c37 juga merupakan bilangan kuadrat mantap: c372 = aa0c37, dan hasil penjumlahan digit-digitnya adalah c+3+7=18 di basis bilangan yang sama. Huruf a, b, c dan d digunakan untuk melambangkan 10, 11, 12 dan 13 secara berurutan, dengan cara perlakuan yang sama dengan sistem bilangan heksadesimal.
Untuk 1 ≤ n ≤ 9, hasil penjumlahan dari semua digit-digit pada bilangan kuadrat mantap dengan n-buah digit pada sistem bilangan basis 14 adalah 2d8 (582 dalam desimal). Bilangan kuadrat mantap dengan angka 0 di depan tidak diperbolehkan.
Carilah hasil penjumlahan semua digit-digit dari bilangan kuadrat mantap dengan n-buah digit dalam sistem bilangan basis 14 untuk
1 ≤ n ≤ 10000 (desimal) dan berikan jawaban Anda dalam bentuk basis 14 dengan huruf kecil, jika memerlukan huruf.
Answer: aff724582e583649876f518f9b340a69
Soal 285
Albert memilih sebuah bilangan bulat positif k, kemudian dua bilangan real a, b dipilih secara acak pada interval [0,1] dengan sebaran uniform.
Kemudian dihitung akar kuadrat dari hasil penjumlahan (k·a+1)2 + (k·b+1)2 dan dibulatkan ke bilangan bulat terdekat. Jika hasilnya sama dengan k, Albert mendapatkan k poin; jika hasilnya tidak sama, ia tidak mendapatkan nilai.
Sebagai contoh, jika k = 6, a = 0.2 dan b = 0.85, maka (k·a+1)2 + (k·b+1)2 = 42.05.
Akar kuadrat dari 42.05 adalah 6.484... dan setelah dibulatkan ke bilangan bulat terdekat, hasil tersebut menjadi 6.
Hasil ini sama dengan k, sehingga ia mendapatkan 6 poin.
Dapat dibuktikan apabila ia bermain 10 putaran dengan k = 1, k = 2, ..., k = 10, maka nilai harapan (expected value) dari total skor yang kemungkinan akan dicapai, dibulatkan hingga lima angka di belakang koma, adalah 10.20914.
Jika ia bermain sebanyak 105 putaran dengan k = 1, k = 2, k = 3, ..., k = 105, berapakah nilai harapan (expected value) dari total skornya, dibulatkan hingga lima angka di belakang koma?
Answer: bbae95d0ce2999cae57782c3746aecb6
Soal 286
Barbara adalah seorang ahli matematika dan juga seorang pemain basket. Ia menemukan bahwa kemungkinan untuk mencetak nilai saat melakukan shooting bola dari jarak x adalah (1 - x/q), dimana q adalah konstanta bilangan real lebih besar dari 50.
Setiap latihan, ia mencoba melakukan shooting dari jarak x = 1, x = 2, ..., x = 50 dan, bedasarkan catatan dia, ia memiliki tepat 2 % peluang untuk mencetak skor dengan total nilai persis 20 poin.
Carilah nilai q dan berikan jawaban Anda dibulatkan hingga 10 angka di belakang koma.
Answer: cc5a1ef0deabf698733bcef4f1149498
Soal 287
Algoritma quadtree encoding memungkinkan kita untuk dapat menuliskan gambar hitam dan putih berukuran 2N×2N sebagai barisan bit (0 dan 1). Barisan tersebut dibaca dari kiri ke kanan seperti ini:
- bit pertama melambangkan semua daerah 2N×2N;
- "0" melambangkan pemisahan:
daerah berukuran 2n×2n harus dipisah menjadi 4 sub daerah dengan ukuran 2n-1×2n-1,
bit selanjutnya melambangkan sub daerah kiri atas, kanan atas, kiri bawah, dan kanan bawah secara berurutan; - "10" melambangkan bahwa daerah tersebut berisi hanya piksel hitam;
- "11" melambangkan bahwa daerah tersebut berisis hanya piksel putih.
Perhatikan gambar berukuran 4×4 berikut (tanda berwarna menunjukkan tempat dimana proses pemisahan dapat berlangsung):

Gambar ini dapat dituliskan dengan beberapa barisan, sebagai contoh :
"0100101111101110", dengan panjang 16, yang dimana merupakan panjang barisan terpendek untuk gambar ini.
Untuk bilangan bulat positif N, dinyatakan DN sebagai gambar berukuran 2N×2N dengan aturan pewarnaan:
- piksel dengan koordinat x = 0, y = 0 melambangkan piksel paling kiri bawah,
- jika (x - 2N-1)2 + (y - 2N-1)2 ≤ 22N-2 maka piksel tersebut berwarna hitam,
- jika tidak, piksel tersebut bewarna putih.
Berapakah panjang barisan terpendek yang dapat menggambarkan gambar D24 ?
Answer: 6c2beec8a6c0bc788d5e45c317b0d7ca
Soal 288
Untuk setiap bilangan prima p hasil N(p,q) dinyatakan dengan
N(p,q) = ∑n=0 sampai q Tn*pn
dengan Tn dibuat menggunakan rumus pembuat bilangan acak berikut:
S0 = 290797
Sn+1 = Sn2 mod 50515093
Tn = Sn mod p
Misal Nfac(p,q) adalah faktorial dari N(p,q).
Misal NF(p,q) adalah banyaknya faktor p pada Nfac(p,q).
Diketahui NF(3,10000) mod 320=624955285.
Carilah NF(61,107) mod 6110
Answer: 192bf4aa33ea85e922d583f60fe99955
Soal 289
Misal C(x,y) adalah lingkaran yang melalui titik (x, y), (x, y+1), (x+1, y) dan (x+1, y+1).
Untuk bilangan bulat m dan n, misal E(m,n) adalah konfigurasi yang dibentuk dari lingkaran m·n:
{ C(x,y): 0 ≤ x < m, 0 ≤ y < n, x dan y adalah bilangan bulat }
Sebuah siklus Eulerian pada E(m,n) adalah lintasan tertutup yang melalui setiap busur persis satu kali.
Banyak sekali lintasan yang memungkinkan pada E(m,n), namun kita hanya tertarik pada lintasan yang tidak memotong dirinya sendiri:
Sebuah lintasan yang tidak memotong dirinya sendiri, hanya menyinggung dirinya pada titik potong lingkaran, namun tidak pernah memotong jalur itu sendiri.
Gambar berikut ini menunjukkan E(3,3) dan juga merupakan sebuah contoh dari lintasan Eulerian yang tidak memotong dirinya sendiri.

Misal L(m,n) adalah banyaknya lintasan Eulerian yang tidak memotong dirinya sendiri pada E(m,n).
Sebagai contoh, L(1,2) = 2, L(2,2) = 37 dan L(3,3) = 104290.
Carilah L(6,10) mod 1010.
Answer: 9fa32696df356b3d41faa7dd278c88a9
Soal 290
Berapa banyak bilangan bulat 0 ≤ n < 1018 yang memiliki sifat hasil penjumlahan digit-digit dari n sama dengan hasil penjumlahan digit-digit dari 137n?
Answer: 8246684fec8ece9f0ee3c9898c8c9d6a
Soal 291
Sebuah bilangan prima p akan disebut sebagai prima Panaitopol jika  untuk
untuk
x dan y bilangan bulat.
Carilah berapa banyak prima Panaitopol yang kurang dari 5×1015.
Answer: 15d4b4d97452ca7d219e3fa72f6b7aef
Soal 292
Kita akan menyatakan sebuah poligon pythagoras sebagai sebuah poligon konveks dengan sifat-sifat berikut:
- terdapat setidakny a tiga titik sudut,
- tidak ada tiga titik sudut yang terletak dalam satu garis lurus,
- setiap titik sudut mempunyai koordinat bilangan bulat,
- setiap garis memiliki panjang bilangan bulat.
Jika diberikan bilangan bulat n, dapat dinyatakan P(n) sebagai banyaknya poligon pythagoras berbeda yang memiliki keliling ≤ n.
Poligon pythagoras akan dianggap berbeda selama bukan merupakan hasil translasi dari poligon lain.
Diketahui P(4) = 1, P(30) = 3655 dan P(60) = 891045.
Carilah P(120).
Answer: 27f50f02ef10f170379b144435e0144b
Soal 293
Sebuah bilangan genap positif N dapat dikatakan admissible, jika angka tersebut merupakan bilangan 2x {x ∈ bilangan asli}, atau faktor primanya merupakan bilangan prima berbeda yang berurutan.
Dua belas angka admissible pertama adalah 2,4,6,8,12,16,18,24,30,32,36,48.
Jika N admissible, maka dapat ditentukan bilangan bulat terkeci M > 1 yang memenuhi N+M ∈ prima, M akan disebut angka pseudo-Fortunate untuk N..
Sebagai contoh, N=630 adalah admissible, karena angka tersebut merupakan bilangan genap dan faktor primanya adalah berurutan, yaitu 2, 3, 5, dan 7.
Angka prima selanjutnya setelah 631 adalah 641; sehingga bilangan pseudo-Fortunate untuk 630 adalah M=11.
Contoh lainnya, bilangan pseudo-Fortunate dari N=16 adalah M=3.
Carilah jumlah dari semua bilangan pseudo-Fortunate berbeda untuk bilangan admissible N kurang dari 109.
Answer: db116b39f7a3ac5366079b1d9fe249a5
Soal 294
Untuk bilangan bulat k, dinyatakan d(k) sebagai hasil penjumlahan digit-digit dari k dalam representasi desimalnya seperti biasa. Sehingga d(42) = 4+2 = 6.
Untuk bilangan bulat n, dinyatakan S(n) sebagai banyaknya bilangan bulat k < 10n yang memenuhi sifat berikut:
- k habis dibagi 23 dan
- d(k) = 23.
Diketahui S(9) = 263626 dan S(42) = 6377168878570056. </p>
Carilah S(1112) dan berikan jawaban Anda yang telah di mod 109.
Answer: aefe049404a284c7d27fab3887c6c4a2
Soal 295
Kita akan menyebut daerah konveks yang dibatasi oleh dua lingkaran sebagai sebuah lubang lentikular jika:
- Pusat kedua lingkaran pada titik-titik dengan koordinat bilangan bulat.
- Dua lingkaran berpotongan pada dua titik dengan koordinat bilangan bulat berbeda.
- Bagian dalam dari daerah konveks yang dibatasi oleh kedua lingkaran tidak terdapat titik koordinat bilangan bulat.
Perhatikan lingkaran:
C0: x2+y2=25
C1: (x+4)2+(y-4)2=1
C2: (x-12)2+(y-4)2=65
Lingkaran C0, C1 dan C2 digambarkan pada gambar berikut.

C0 dan C1 membentuk lubang lentikular, hal yang sama juga terjadi pada lingkaran C0 dan C2.
Kita akan menyebut pasangan berurutan dari bilangan real positif (r1, r2) sebagai sebuah pasangan lentikular jika terdapat dua lingkaran dengan panjang jari-jari r1 dan r2 yang membentuk lubang lentikular. Kita dapat membuktikan bahwa (1, 5) dan (5, √65) adalah pasangan lentikular pada contoh di atas.
Misal L(N) adalah banyaknya pasangan lentikular berbeda (r1, r2) dimana 0 < r1 ≤ r2 ≤ N.
Kita dapat membuktikan bahwa L(10) = 30 dan L(100) = 3442.
Carilah L(100 000).
Answer: 5beaace6425205fe879116ee07dae961
Soal 296
Diketahui sebuah segitiga ABC memiliki panjang sisi bilangan bulat dengan BC ≤ AC ≤ AB.
k adalah garis bagi dari sudut ACB.
m adalah garis singgung pada titik C pada lingkaran luar segitiga ABC.
n adalah garis yang sejajar dengan m dan melalui B.
Perpotongan antara n dan k akan disebut E.

Berapa banyak segitiga ABC dengan panjang keliling kurang dari 100 000 yang ada, yang memiliki panjang BE berupa bilangan bulat?
Answer: 45986a4405b2dd6c163516319e0c4a1b
Soal 297
Setiap suku baru dalam barisan Fibonacci dibentuk dengan menjumlahkan dua suku sebelumnya.
Dimulai dengan 1 dan 2, 10 suku pertamanya adalah: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
Setiap bilangan bulat positif dapat ditulis sebagai hasil penjumlahan suku-suku tidak berurutan pada barisan Fibonacci. Sebagai contoh, 100 = 3 + 8 + 89.
Penjumlahan semacam itu desebut sebagai representasi Zeckendorf dari suatu bilangan.
Untuk setiap bilangan bulat n>0, dinyatakan z(n) adalah banyaknya suku pada representasi Zeckendorf untuk n.
Sehingga, z(5) = 1, z(14) = 2, z(100) = 3 dan sebagainya.
Juga, untuk 0<n<106, ∑ z(n) = 7894453.
Carilah ∑ z(n) untuk 0<n<1017.
Answer: d3fd75f5447698748a826562750a1986
Soal 298
Larry dan Robin memainkan sebuah permainan ingatan yang melibatkan barisan bilangan acak antara 1 dan 10, yang disebutkan satu persatu. Setiap pemain dapat mengingat sampai 5 buah bilangan sebelumnya. Saat bilangan yang disebutkan ada pada ingatan salah satu pemain, pemain tersebut mendapatkan poin. Jika tidak, pemain tersebut menambahkan bilangan yang baru disebutkan tadi ke ingatannya, dan menghapus bilangan lain jika ingatannya sudah penuh.
Kedua pemain memulai permainan dengan ingatan kosong. Kedua pemain selalu menambahkan bilangan baru ke ingatan mereka, namun mereka menggunakan strategi yang berbeda untuk memilih bilangan mana yang harus dihapus:
Strategi Larry adalah menghapus bilangan yang paling lama tidak disebut.
Strategi Robin adalah menghapus bilangan yang telah paling lama berada di ingatannya.
Contoh permainan:
| Putaran | Bilangan yang disebut |
Ingatan Larry |
Skor Larry |
Ingatan Robin |
Skor Robin |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 |
| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
Jika skor Larry dilambangkan dengan L dan skor Robin dilambangkan dengan R, berapakah nilai harapan (expected value) dari |L-R| setelah 50 kali putaran? Berikan jawaban Anda yang dibulatkan hingga delapan angka di belakang koma dengan format x.xxxxxxxx .
Answer: d078fd564995aa2a813a29f44ad79611
Soal 299
Empat buah titik dengan koordinat bilangan bulat dipilih:
A(a, 0), B(b, 0), C(0, c) dan D(0, d),
dengan 0 < a < b dan 0 < c < d.
Titik P, yang juga memiliki koordinat bilangan bulat, dipilih dari garis AC sehingga ketiga segitiga ABP, CDP dan BDP adalah sebangun similar.

Mudah untuk membuktikan bahwa tiga buah segitiga sebangun, namun hanya jika a=c.
Sehingga, diketahui a=c, kita akan mencari triplet (a,b,d) sehingga setidaknya terdapat satu titik P (dengan koordinat bilangan bulat) yang ada pada garis AC, yang akan membuat tiga segitiga ABP, CDP dan BDP semuanya sebangun.
Sebagai contoh, jika (a,b,d)=(2,3,4), dapat dengan mudah dibuktikan bahwa titik P(1,1) memenuhi kondisi di atas. Perlu diingat bahwa triplet (2,3,4) dan (2,4,3) dianggap berbeda, walaupun titik P(1,1) berlaku untuk keduanya.
Jika b+d < 100, maka akan terdapat 92 triplet berbeda (a,b,d) yang memiliki titik P.
Jika b+d < 100 000, maka akan terdapat 320471 triplet berbeda (a,b,d) yang memiliki titik P.
Jika b+d < 100 000 000, berapa banyak triplets berbeda (a,b,d) yang memiliki titik P?
Answer: fb8f093361a6db56c8a1d1661ab229cd
Soal 300
Pada bentuk yang paling sederhana, kita dapat menganggap protein sebagai barisan yang terdiri dari unsur hidrofobik (H) dan polar (P), sebagai contoh HHPPHHHPHHPH.
Untuk soal ini, arah hadap dari protin adalah penting untuk diperhatikan; sebagai contoh HPP dianggap berbeda dengan PPH. Sehingga, terdapat 2n protein berbeda yang terdiri dari n buah unsur.
Saat protein bertemu dengan protein lainnya di alam, mereka selalu melipat dirinya sedemikian sehingga banyaknya titik temu H-H menjadi sebanyak mungkin, karena akan menguntungkan jika ditinjau dari energinya.
Sebagai hasilnya, unsur H cenderung berkumpul di bagian dalam, sedangkan unsur P pada bagian luar.
Tentu saja protein alami berbentuk tiga dimensi, namun kita hanya akan memperhitungkan protein yang dilipat dalam dua dimensi.
Gambar berikut ini menunjukkan dua kemungkinan cara sebuah protein dapat dilipat (titik temu H-H ditunjukkan dengan titik berwarna merah).

Lipatan sebelah kiri hanya memiliki enam buah titik temu H-H, sehingga lipatan ini tidak akan terjadi secara alamiah.
Di sisi lain, lipatan di sebelah kanan memiliki sembilan titik temu H-H, dimana merupakan jumlah yang optimal untuk protein ini.
Jika diasumsikan bahwa unsur H dan P memiliki peluang yang sama untuk muncul di posisi manapun pada barisan, jumlah rata-rata dari titik temu H-H pada pelipatan barisan protein acak yang sudah optimal dengan panjang barisan protein 8, adalah 850 / 28=3.3203125.
Berapakah jumlah rata-rata titik temu H-H pada pelipatan optimal dari barisan protein acak dengan panjang barisan protein 15?
Berikan jawaban Anda menggunakan sebanyak mungkin angka di belakang koma, untuk memberikan hasil yang seakurat mungkin.
Answer: 5a0d6315bc18279c46a1fb8cbd2f16b5
Soal 301
Nim adalah sebuah permainan yang dimainkan menggunakan tumpukan batu, dimana dua pemain mengambil batu sebanyak yang diinginkannya dari tumpukan manapun, sampai tidak ada batu tersisa.
Kita akan memainkan permainan Nim versi normal tiga tumpukan, yang memiliki aturan sebagai berikut:
- Saat permaian dimulai, terdapat tiga tumpukan batu.
- Pada gilirannya, seorang pemain mengambil berapapun jumlah batu dari salah satu tumpukan.
- Pemain pertama yang tidak bisa mengambil batu lagi (karena tidak ada batu tersisa) adalah pemain yang kalah.
Jika (n1,n2,n3) melambangkan Nim dengan masing-masing tumpukan memiliki n1, n2 dan n3 buah batu, maka terdapat fungsi sederhana X(n1,n2,n3) — yang bisa anda cari atau anda coba simpulkan sendiri — yang akan menghasilkan:
- nol jika, dengan strategi yang sempurna, pemain yang akan memulai permainan pertama kali akan kalah; atau
- bukan nol jika, dengan strategi yang sempurna, pemain yang akan memulai permainan pertama kali akan menang.
Sebagai contoh X(1,2,3) = 0 karena, tidak peduli apapun yang dilakukan oleh pemain pertama, lawannya selalu akan dapat melakukan gerakan yang akan meninggalkan dua buah tumpukan dengan jumlah batu yang sama, yang dimana setiap gerakan pemain pertama akan selalu dapat diikuti oleh lawannya sampai tidak ada batu tersisa; sehingga pemain pertama akan kalah. Untuk mengambarkan:
- Pemain pertama melakukan gerakan sehingga tumpukan menjadi (1,2,1)
- Pemain kedua merubah tumpukan menjadi (1,0,1)
- Pemain pertama merubah tumpukan menjadi (0,0,1)
- Pemain kedua merubah tumpukan menjadi (0,0,0), dan kemudian ia menang.
Untuk berapa banyak bilangan bulat n ≤ 230 yang menyebabkan X(n,2n,3n) = 0 ?
Answer: f47b7d975a5ebd3b66af0968ef5e1cdb
Soal 302
Sebuah bilangan bulat n disebut kuat jika p2 dapat membagi habis n dan p adalah semua faktor prima dari n.
Sebuah bilangan bulat positif n disebut sebagai sebuah pangkat sempurna jika n dapat dinyatakan sebagai hasil perpangkatan bilangan bulat positif lain.
Sebuah bilangan bulat positif n disebutr sebagai sebuah bilangan Achilles jika n adalah bilangan kuat namun bukan merupakan bilangan pangkat sempurna. Sebagai contoh, 864 dan 1800 adalah bilangan Achilles: 864 = 25·33 dan 1800 = 23·32·52.
Kita akan menyebut sebuah bilangan bulat positif S sebagai bilangan Achilles kuat jika S dan φ(S) keduanya adalah bilangan Achilles.1
Sebagai contoh, 864 adalah sebuah bilangan Achilles kuat: φ(864) = 288 = 25·32. Namun, 1800 bukanlah bilangan Achilles kuat karena: φ(1800) = 480 = 25·31·51.
Terdapat 7 buah bilangan Achilles kuat kurang dari 104 dan 656 buah yang kurang dari 108.
Berapakah banyaknya bilangan Achilles kuat yang kurang dari 1018?
1 φ menyatakan fungsi totient Euler's.
Answer: 1ea8b8d64cead5149721a128b0de378c
Soal 303
Untuk bilangan bulat n, dinyatakan f(n) sebagai bilangan positif kelipatan n terkecil, yang ditulis di basis 10, dan hanya menggunakan digit ≤ 2.
Sehingga f(2)=2, f(3)=12, f(7)=21, f(42)=210, f(89)=1121222.
Juga,  .
.
Carilah  .
.
Answer: b904a0b3d922e628a828e744ee7d3a60
Soal 304
Untuk setiap bilangan bulat positif n fungsi next_prime(n) akan menghasilkan bilangan prima terkecil p
sehingga p>n.
Barisan a(n) dinyatakan dengan:
a(1)=next_prime(1014) dan a(n)=next_prime(a(n-1)) untuk n>1.
Barisan fibonacci f(n) dinyatakan dengan: f(0)=0, f(1)=1 dan f(n)=f(n-1)+f(n-2) untuk n>1.
Barisan b(n) dinyatakan sebagai f(a(n)).
Carilah ∑b(n) untuk 1≤n≤100 000. Berikan jawaban Anda yang telah di mod 1234567891011.
Answer: 499427a3e4bf9ad34a6df3056604b4c1
Soal 305
Kita akan menyebut S sebagai deretan (tak hingga) yang dibuat dengan menyatukan bilangan bulat positif berurutan (dimulai dari 1) yang ditulis dalam basis 10.
Sehingga, S = 1234567891011121314151617181920212223242...
Dapat dengan mudah terlihat bahwa semua bilangan akan muncul sebanyak tak hingga kali pada S.
Kita akan menyebut f(n) sebagai posisi mulai munculnya angka n yang ke n-kali di S.
Sebagai contoh, f(1)=1, f(5)=81, f(12)=271 dan f(7780)=111111365.
Carilah ∑f(3k) untuk 1≤k≤13.
Answer: 9def85298f598867d361e4afca8cdd96
Soal 306
Permainan berikut ini adalah contoh klasik dari Teori Permainan Kombinatorial:
Dua pemain memulai permainan dengan sepotong kertas yang memiliki n buah persegi putih, dan mereka melakukan permainan secara bergiliran.
Pada setiap giliran, seorang pemain memilih dua persegi putih yang bersebelahan kemudian mewarnai kedua kotak tersebut menjadi hitam.
Pemain pertama yang tidak bisa melakukan gerakan lagi dianggap kalah.
- Jika n = 1, maka tidak ada gerakan yang valid, sehingga pemain pertama langsung kalah.
- Jika n = 2, maka hanya terdapat satu gerakan yang memungkinkan, setelah itu pemain kedua akan kalah.
- Jika n = 3, akan terdapat dua gerakan yang mungkin dilakukan, namun kedua gerakan tersebut akan menyebabkan pemain kedua kalah.
- Jika n = 4, terdapat tiga gerakan yang mungkin dilakukan oleh pemain pertama; ia dapat memenangkan permainan dengan mewarnai dua persegi di tengah.
- Jika n = 5, terdapat empat gerakan yang mungkin dilakukan oleh pemain pertama (ditunjukkan pada gambar berikut denagn warna merah); namun tidak peduli apapun yang ia lakukan, pemain kedua (biru) akan selalu menang.

Sehingga, untuk 1 ≤ n ≤ 5, terdapat 3 buah nilai n yang akan membuat pemain pertama menjadi pemenang.
Hal yang sama, untuk 1 ≤ n ≤ 50, terdapat 40 buah nilai n yang akan membuat pemain pertama menjadi pemenang.
Untuk 1 ≤ n ≤ 1 000 000, berapa banyak nilai n yang ada, yang akan menyebabkan pemain pertama menang?
Answer: 394d602ba21e30693db90c9ecd4bd3a2
Soal 307
k buah kecacatan tersebar secara acak pada n buah chip integrated-circuit yang diproduksi oleh sebuah pabrik (beberapa kecacatan dapat ditemui dalam satu chip, dan setiap kecacatan berbeda dengan kecacatan lainnya).
p(k,n) adalah peluang terdapat sebuah chip yang memiliki setidaknya 3 kecacatan.
Sebagai contoh p(3,7) ≈ 0.0204081633.
Carilah p(20 000, 1 000 000) dan berikan jawaban Anda yang dibulatkan hingga 10 angka di belakang koma dengan format 0.abcdefghij
Answer: 0c49094fa750365e13bb20ec4a158b6d
Soal 308
Sebuah program ditulis dalam bahasa pemrograman Fractran yang terdiri dari daftar pecahan.
Bagian dalam dari Fractran Virtual Machine mengandung bilangan bulat positif, yang di setel untuk mengeluarkan berbagai bilangan. Setiap hasil iterasi dari program Fractran didapatkan dengan mengalikan bilangan bulat di dalam dengan pecahan pertama pada daftar yang akan menghasilkan bilangan bulat juga setelah dikalikan.
Sebagai contoh, salah satu program Fractran yang ditulis oleh John Horton Conway untuk membentuk bilangan prima terdiri dari 14 buah pecahan berikut:
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
. |
Dimulai dengan bilangan bulat 2, iterasi selanjutnya yang sesuai dengan aturan di atas akan menghasilkan barisan:
15, 825, 725, 1925, 2275, 425, ..., 68, 4, 30, ..., 136, 8, 60, ..., 544, 32, 240, ...
Bilangan perpangkatan 2x yang muncul di barisan ini adalah 22, 23, 25, ...
Dapat ditunjujkkan bahwa semua x dari barisan ini merupakan bilangan prima, dan semua x barisan ini, muncul secara berurutan!
Jika seseorang mengguanakn program Fractran di atas untuk menyelesaikan Project Euler Soal 7 (mencari pilangan prima ke-10001), berapa banyak iterasi yang dibutuhkan sampai program menghasilkan 2bilangan prima ke-1000 ?
Answer: 43e736dfc6478a52653814248a71771d
Soal 309
Dalam permasalhan "Tangga Menyilang" klasik, kita diberikan informasi panjang dari dua buah tangga sebagai x dan y, kedua tangga bersandar pada tembok di seberangnya dan ujung-ujungnya berada di tepi jalan sempit. Kita juga diberikan informasi tentang tinggi titik persilangan tangga h jika diukur dari jalan, dan kita diminta untuk mencari lebar jalan (w).

Di soal ini, kita hanya akan melihat kondisi dimana ke empat variabel adalah bilangan bulat positif.
Sebagai contoh, jika x = 70, y = 119 dan h = 30, kita dapat menghitung w = 56.
Kenyataannya, untuk bilangan bulat x, y, h dan 0 < x < y < 200, hanya ada lima buah triplet (x,y,h) yang akan menghasilkan solusi bilangan bulat untuk w:
(70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35) and (119, 175, 40).
Untuk bilangan bulat x, y, h dan 0 < x < y < 1 000 000, berapa banyak triplet (x,y,h) yang akan menghasilkan solusi bilangan bulat untuk w?
Answer: 0875415a84bfe8bc237dcfc6b440d263
Soal 310
Alice dan Bob memainkan permainan Nim Kuadrat.
Nim Kuadrat sebenarnya hampir sama dengan permainan tiga tumpuk Nim biasa, namun kali ini para pemain hanya diperbolehkan untuk mengambil batu sebanyak bilangan kuadrat dari tumpukan.
Banyaknya batu pada ketiga tumpukan dituliskan secara berurutan dengan triplet (a,b,c).
Jika 0≤a≤b≤c≤29 maka banyaknya posisi kalah untuk pemain kedua adalah 1160.
Carilah banyaknya posisi kalah untuk pemain kedua jika 0≤a≤b≤c≤100 000.
Answer: 6b94f848996393eef163add4d17360c7
Soal 311
ABCD adalah bangun bersisi empat konveks, dengan panjang sisi berupa bilangan bulat yaitu 1 ≤ AB < BC < CD < AD.
BD juga mempunyai panjang berupa bilangan bulat. O adalah titik tengah dari BD. AO juga mempunyai panjang berupa bilangan bulat.
Kita akan menyebut ABCD sebagai sebuah bangun sisi-empat biclinic bilangan bulat jika AO = CO ≤ BO = DO.
Sebagai contoh, bangun sisi empat berikut ini adalah bangun sisi-empat biclinic bilangan bulat:
AB = 19, BC = 29, CD = 37, AD = 43, BD = 48 dan AO = CO = 23.

B(N) adalah banyaknya bangun sisi-empat biclinic bilangan bulat ABCD berbeda yang memenuhi AB2+BC2+CD2+AD2 ≤ N.
Kita dapat membuktikan bahwa B(10 000) = 49 dan B(1 000 000) = 38239.
Carilah B(10 000 000 000).
Answer: 36115d4f7dc07eea106d78e8431868e6
Soal 312
- Sebuah grafik Sierpiński dengan orde 1 (S1) adalah sebuah segitiga sama sisi.
- Sn+1 didapatkan dari Sn dengan meletakan tiga buah salinan dari Sn sehingga setiap dua buah salinan memiliki satu titik pojok yang bertemu.

Misal C(n) adalah banyaknya siklus yang berputar persis satu kali dan melalui semua titik pada Sn.
Sebagai contoh, C(3) = 8 karena terdapat delapan buah jalur yang bisa digambar pada S3, seperti ditunjukkan pada gambar berikut:

Juga dapat dibuktikan bahwa :
C(1) = C(2) = 1
C(5) = 71328803586048
C(10 000) mod 108 = 37652224
C(10 000) mod 138 = 617720485
Carilah C(C(C(10 000))) mod 138.
Answer: 535113d1a81f421fe814d48205dac570
Soal 313
Dalam permainan menggeser, sebuah potongan boleh bergeser secara horizontal ataupun vertikal ke tempat yang kosong. Sasaran dari permainan ini adalah untuk memindahkan potongan merah dari pojok kiri atas ke pojok kanan bawah; ruang kosong selalu berada pertama kali di pojok kanan bawah. Sebagai contoh, gambar-gambar berikut ini akan menunjukkan bahwa permainan dapat diselesaikan dalam lima langkah untuk kisi berukuran 2 x 2.

S(m,n) menunjukkan jumlah gerakan minimal untuk menyelesaikan permaian pada kisi berukuran m x n. Sebagai contoh, dapat dibuktikan bahwa S(5,4) = 25.

Terdapat persis 5482 ukuran kisi dimana S(m,n) = p2, dimana p < 100 adalah bilangan prima.
Berapakah banyaknya ukuran kisi yang memenuhi S(m,n) = p2, dimana p < 106 adalah bilangan prima?
Answer: 2468d42fa1c7f61547ce71c9826218ea
Soal 314
Bulan telah dibuka untuk umum, dan kita dapat memiliki tanah di sana dengan gratis, namun ada satu permasalahan. Anda harus membuat tembok di sekeliling tanah yang Anda tempati, dan untuk membangun tembok di bulan memerlukan biaya yang besar. Setiap negara telah diberikan jatah tanah berukuran 500 m x 500 m, namun mereka hanya dapat menggunakan wilayah yang dibatasi oleh dinding. 251001 buah tiang telah diletakkan pada tanah membentuk petak-petak dengan jarak antar tiang 1 meter. Dinding harus dibentuk dari sambungan garis-garis lurus hingga tertutup, dan setiap garis dinding dapat dibentuk dari tiang ke tiang.
Negara yang besar tentu saja akan membuat dinding sepanjang 2000 m menutup semua wilayah yang menjadi jatahnya dengan luas 250 000 m2. Adipati Grand Fenwick, memiliki dana yang terbatas, dan ia meminta anda (sebagai Programmer Kerajaan) untuk menghitung bentuk dinding seperti apa yang akan menghasilkan perbandingan terbaik antara luas yang ditutupi dinding/panjang dinding.
Anda telah melakukan sedikit perhitungan pada selembar kertas.
Untuk dinding dengan panjang 2000 yang menutupi wilayah seluas 250 000 m2, perbandingan
luas yang ditutupi dinding/panjang dinding adalah 125.
Walaupun tidak diperbolehkan, namun terdapat ide untuk membuat hasil yang lebih baik: yaitu jika kita membangun dinding berbentuk lingkaran yang menyinggung keempat sisi persegi, luas wilayah yang dibatasi dinding akan menjadi π*2502 m2 dan keliilngnya akan menjadi π*500 m, sehingga perbandingan luas yang ditutupi dinding/panjang dinding juga 125.
Tetapi, jika Anda memotong dari pinggiran persegi empat buah segitiga dengan panjang sisi 75 m, 75 m dan 75√2 m luas wilayah yang dibatasi dinding akan menjadi 238750 m2 dan kelilingnya menjadi 1400+300√2 m. Sehingga bentuk ini akan memberikan perbandingan luas yang ditutupi dinding/panjang dinding sebesar 130.87, dimana hasil ini lebih baik.

Carilah nilai perbandingan maksimum dari luas yang ditutupi dinding/panjang dinding.
Berikan jawaban Anda dibulatkan hingga 8 angka di belakang koma dengan format abc.defghijk.
Answer: aa457cae6f67945d50683a85a9b70230
Soal 315

Sam dan Max diminta untuk mengubah dua buah jam digital menjadi dua buah jam "akar kuadrat digital".
Jam akar kuadrat digital adalah sebuah jam yang menghitung akar kuadrat tahap demi tahap.
Saat jam tersebut diberikan suatu bilangan, jam tersebut akan menunjukkan bilangan tersebut, dan kemudian akan mulai melakukan perhitungan, kemudian ia akan segera menunjukkan semua hasil perhitungan terus-menerus sampai selesai.
Sebagai contoh, jika jam diberikan bilangan 137, maka jam tersebut akan menunjukkan: "137" → "11" → "2" dan kemudian jam tersebut akan mati, menunggu angka selanjutnya.
Setiap angka digital dapat dibentuk dari beberapa segmen lampu: tiga buah segmen horizontal (atas, tengah, bawah) dan empat buah segmen vertikal (kiri atas, kanan atas, kiri bawah, kanan bawah).
Angka "1" dapat dibentuk dengan menghidupkan lampu vertikal kanan atas dan kanan bawah, Angka "4" dapat dibentuk dengan menghidupkan lampu horizontal tengah dan vertikal kiri atas, kanan atas, dan kanan bawah. Angka "8" dibentuk dengan menghidupkan semua segmen lampu.
Jam tersebut hanya mengkonsumsi energi jika ada segmen lampu yang diubah kondisinya antara menyala/mati.
Untuk menyalakan lampu membentuk angka "2" akan memerlukan 5 transisi lampu, dimana angka "7" hanya memerlukan 4 transisi lampu.
Sam dan Max membuat dua jam berbeda.
Jam buatan Sam saat diberikan sebuah bilangan, sebagai contoh bilangan 137: jam tersebut akan menunjukkan "137", kemudian semua lampu akan dimatikan, kemudian lampu untuk membentuk bilangan selanjutnya ("11") dihidupkan, kemudian semua lampu dimatikan lagi dan akhirnya lampu untuk membentuk bilangan terakhir ("2") dihidupkan dan, setelah beberapa saat, semua lampu dimatikan.
Sebagai contoh, untuk bilangan 137, jam buatan Sam memerlukan:
| "137" | : | (2 + 5 + 4) × 2 = 22 transisi ("137" nyala/mati). |
| "11" | : | (2 + 2) × 2 = 8 transisi ("11" nyala/mati). |
| "2" | : | (5) × 2 = 10 transisi ("2" nyala/mati). |
Jam buatan Max bekerja dengan cara yang berbeda. Bukan dengan mematikan semua lampu, namun dengan cara yang cukup cerdas, yaitu dengan cara hanya mematikan lampu yang tidak diperlukan untuk bilangan selanjutnya.
Untuk bilangan 137, jam buatan Max memerlukan:
| "137" |
: |
2 + 5 + 4 = 11 transisi ("137" hidup) 7 transisi (untuk mematikan segmen lampu yang tidak diperlukan pada bilangan "11"). |
| "11" |
: |
0 transisi (bilangan "11" sudah menyala secara benar) 3 transisi (untuk mematikan angka "1" yang pertama dan bagian bawah dari angka "1" yang kedua; karena lampu atasnya diperlukan untuk angka "2"). |
| "2" |
: |
4 transisi (untuk menghidupkan segmen lampu yang diperlukan untuk membentuk angka "2") 5 transisi (untuk mematikan angka "2"). |
Tentu saja, jam buatan Max mengkonsumsi energi yang lebih sedikit dibandingkan dengan buatan Sam.
Kedua jam diberikan bilangan-bilangan prima antara A = 107 dan B = 2×107.
Carilah perbedaan jumlah transisi yang diperlukan oleh jam buatan Sam dengan jumlah transisi yang diperlukan oleh jam buatan Max.
Answer: 79b587f9c25a72dbe95428e283628421
Soal 316
Misal p = p1 p2 p3 ... adalah sebuah barisan tak hingga dari digit-digit acak, yang dipilih dari {0,1,2,3,4,5,6,7,8,9} dengan peluang yang sama.
Dapat terlihat bahwa p mewakili sebuah bilangan real 0.p1 p2 p3 ....
Dapat juga terlihat bahwa apabila kita memilih sebuah bilangan real secara acak pada interval [0,1) sama dengan memilih barisan tak hingga dengan digit-digit acak yang dipilih dari {0,1,2,3,4,5,6,7,8,9} dengan peluang yang sama.
Untuk setiap bilangan bulat positif n dengan d buah digit desimal, k adalah indeks terkecil sehingga
pk, pk+1, ...pk+d-1 adalah digit-digit desimal dari n, dengan urutan yang sama.
Juga, kita misalkan g(n) adalah nilai harapan (expected value) dari k; dapat dibuktikan bahwa g(n) selalu tertentu atau terhingga dan, menariknya, selalu merupakan bilangan bulat.
Sebagai contoh, jika n = 535, maka
untuk p = 31415926535897...., kita dapatkan k = 9
untuk p = 355287143650049560000490848764084685354..., kita dapatkan k = 36
dan sebagainya, dan kita dapat menemukan bahwa g(535) = 1008.
Diberikan  , carilah
, carilah 
Catatan:  adalah fungsi pembulatan ke bawah.
adalah fungsi pembulatan ke bawah.
Answer: 2495e8f6e9d4cdadbf0411144e7180b9
Soal 317
Sebuah petasan meledak pada ketinggian 100 m di atas tanah. Petasan tersebut pecah menjadi banyak sekali pecahan kecil, yang bergerak ke segeala arah; semua pecahan tersebut memiliki kecepatan awal yang sama, yaitu 20 m/s.
Kita asumsikan tidak terdapat gesekan udara saat pecahan petasan bergerak, dan pecahan bergerak di medan gravitasi seragam dengan g=9.81 m/s2.
Carilah volume (dalam m3) dari daerah yang dilalui oleh pecahan-pecahan petasan tersebut sebelum pecahan menyentuh tanah. Berikan jawaban Anda yang dibulatkan hingga empat angka di belakang koma.
Answer: b0e2bec93bfe598ade5d3d1141f76bdd
Soal 318
Perhatikan bilangan real √2+√3.
Saat kita menghitung hasil pemangangkatan genap dari √2+√3
kita dapatkan:
(√2+√3)2 = 9.898979485566356...
(√2+√3)4 = 97.98979485566356...
(√2+√3)6 = 969.998969071069263...
(√2+√3)8 = 9601.99989585502907...
(√2+√3)10 = 95049.999989479221...
(√2+√3)12 = 940897.9999989371855...
(√2+√3)14 = 9313929.99999989263...
(√2+√3)16 = 92198401.99999998915...
Seperti terlihat bahwa bilangan yang dibentuk dari angka sembilan berurutan setelah tanda koma tidak berkurang.
Kenyataannya, dapat dibuktikan bahwa angka-angka di belakang koma dari (√2+√3)2n akan mendekati 1 untuk nilai n yang besar.
Perhatikan bahwa semua bilangan real dengan bentuk √p+√q dengan p dan q berupa bilangan bulat positif dan p<q, sehingga bagian angka di belakang koma dari (√p+√q)2n akan mendekati 1 untuk nilai n yang besar.
Misal C(p,q,n) adalah banyaknya angka sembilan berurutan yang muncul setelah tanda koma dari bentuk desimal
(√p+√q)2n.
Dan misal N(p,q) adalah nilai n minimal sehingga C(p,q,n) ≥ 2011.
Carilah ∑N(p,q) untuk p+q ≤ 2011.
Answer: de358f1c4d6e30c1a4f82c8bc5cedf2d
Soal 319
Misal x1, x2,..., xn adalah barisan dengan panjang n dengan ketentuan:
- x1 = 2
- untuk semua 1 < i ≤ n : xi-1 < xi
- untuk semua i dan j dengan 1 ≤ i, j ≤ n : (xi) j < (xj + 1)i
Hanya terdapat lima buah barisan dengan panjang 2, yaitu:
{2,4}, {2,5}, {2,6}, {2,7} dan {2,8}.
Namun terdapat 293 buah barisan dengan panjang 5; berikut ini adalah tiga buah contohnya:
{2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181}.
Misal t(n) menyatakan banyaknya barisan dengan panjang n.
Anda diberikan informasi bahwa t(10) = 86195 dan t(20) = 5227991891.
Carilah t(1010) dan berikan jawaban Anda yang telah di modulo 109.
Answer: d346ab7d128ee0402820edf5fe4aed30
Soal 320
Misal N(i) adalah bilangan bulat n terkecil, sehingga n! habis dibagi oleh (i!)1234567890
Misal S(u)=∑N(i) untuk 10 ≤ i ≤ u.
S(1000)=614538266565663.
Carilah S(1 000 000) mod 1018.
Answer: 8426f939c3ee410a8c4d43886ef77ccb
Soal 321
Sebuah barisan horizontal berisi 2n + 1 buah persegi memiliki n buah potongan merah diletakkan pada ujungnya, dan n buah potongan biru di ujung satunya lagi, dipisahkan oleh satu buah persegi kosong di tengah-tengahnya. Sebagai contoh, saat n = 3.

Setiap potongan dapat berpindah dari satu persegi ke persegi di sebelahnya (bergeser) atau dapat melompati potongan lain (melompat) selama persegi di sebelah potongan yang ingin dilompati masih kosong.

Misal M(n) menyatakan banyaknya gerakan minimum untuk membalik posisi dari potongan berwarna; yaitu, memindahkan semua potongan merah ke kanan dan semua potongan biru ke kiri.
Dapat dibuktikan bahwa M(3) = 15, dimana bilangan ini juga merupakan bilangan segitiga.
Jika kita membuat barisan bedasarkan nilai n dimana hasil dari M(n) adalah merupakan bilangan segitiga, maka lima suku pertamanya adalah:
1, 3, 10, 22, dan 63, dan hasil penjumlahan mereka akan menjadi 99.
Carilah hasil penjumlahan empat puluh suku pertama dari barisan ini.
Answer: 6d87412130312b01a999225a5fe689b1
Soal 322
Misal T(m, n) adalah banyaknya koefisien penjabaran binomial iCn yang habis dibagi 10 untuk n ≤ i < m(i, m dan n adalah bilangan bulat positif).
Diberikan informasi T(109, 107-10) = 989697000.
Carilah T(1018, 1012-10).
Answer: a75af9d717fa592487fb45e7552204a8
Soal 323
Misal y0, y1, y2,... adalah barisan bilangan bulat acak unsigned 32 bit
(0 ≤ yi < 232, setiap nilai memiliki kemungkinan yang sama).
Untuk barisan xi diberikan aturan rekursif berikut:
- x0 = 0 and
- xi = xi-1 | yi-1, untuk i > 0. ( | adalah operasi bitwise-OR)
Dapat terlihat bahwa akhirnya akan terdapat sebuah indeks N sehingga xi = 232 -1 (yang memiliki bit-pattern semuanya digit satu) untuk semua i ≥ N.
Carilah nilai harapan (expected value) dari N.
Berikan jawaban Anda dibulatkan hingga 10 angka di belakang koma.
Answer: c8f8a7ab17a87f1b17a1f4a86c984ea7
Soal 324
Misal f(n) menyatakan banyaknya cara seseorang dapat mengisi sebuah menara berukuran 3×3×n dengan balok-balok berukuran 2×1×1.
Anda diperbolehkan untuk memutar posisi balok sesuka hati Anda; tetapi, rotasi, refleksi dari menara itu sendiri dianggap berbeda.
Sebagai contoh (dengan q = 100000007) :
f(2) = 229,
f(4) = 117805,
f(10) mod q = 96149360,
f(103) mod q = 24806056,
f(106) mod q = 30808124.
Carilah f(1010000) mod 100000007.
Answer: b8d91b06d43a2ef98a6fcb0be4a6d617
Soal 325
Sebuah permaian dimainkan dengan dua tumpuk batu dan dua orang pemain. Saat gilirannya, seorang pemain mengambil sejumlah batu dari tumpukan yang lebih besar. Banyaknya batu yang diambil harus merupakan bilangan positif dan sama dengan kelipatan jumlah batu di tumpukan yang lebih kecil.
Sebagai contoh, misalkan pasangan bilangan(6,14) menyatakan susunan dengan 6 batu pada tumpukan yang lebih kecil dan 14 batu pada tumpukan yang lebih besar, maka pemain yang sedang mendapat gilirannya dapat mengambil 6 atau 12 buah batu dari tumpukan yang besar.
Pemain yang mengambil semua batu dari tumpukan memenangkan permainan.
Sebuah susunan kemenangan adalah susunan dimana pemain pertama pasti akan menang. Sebagai contoh, (1,5), (2,6) dan (3,12) adalah susunan kemenangan, karena pemain pertama dapat langsung mengambil semua batu pada tumpukan kedua.
Sebuah susunan kekalahan adalah susunan dimana pemain kedua pasti akan menang, tidak peduli apapun yang dilakukan oleh pemain pertama. Sebagai contoh, (2,3) dan (3,4) adalah susunan kekalahan: setiap gerakan yang sah dari pemain pertama pasti akan meninggalkan susunan kemenangan untuk pemain kedua.
Dinyatakan S(N) sebagai hasil penjumlahan dari (xi+yi) untuk semua susunan kekalahan (xi,yi), 0 < xi < yi ≤ N. Dapat dibuktikan bahwa S(10) = 211 dan S(104) = 230312207313.
Carilah S(1016) mod 710.
Answer: 5b1ce9ac67e0ad6690c728ccba6f0070
Soal 326
Misal an adalah barisan rekursif yang dinyatakan oleh:
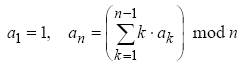
Sehingga 10 sukup ertama dari an adalah: 1,1,0,3,0,3,5,4,1,9.
Misal f(N,M) menyatakan banyaknya pasangan (p,q) sehingga:

Dapat terlihat bahwa f(10,10)=4 dengan pasangan-pasangan (3,3), (5,5), (7,9) dan (9,10).
Anda juga diberikan informasi, yaitu f(104,103)=97158.
Carilah f(1012,106).
Answer: d95dff1a5ceee0064993d98defdd603e
Soal 327
Tiga buah ruangan dihubungkan satu sama lain dengan pintu otomatis.

Setiap pintu dioperasikan dengan kartu keamanan. Sesaat setelah anda memasuki suatu ruangan, pintu akan secara otomatis tertutup, dan kartu keamanan tidak dapat digunakan lagi. Pada ruangan mulai (start), sebuah mesin akan mulai mengeluarkan banyak sekali kartu, namun setiap ruangan (termasuk ruangan start) memiliki alat pemindai, dan jika alat tersebut mendeteksi bahwa Anda memegang lebih dari tiga kartu keamanan, atau jika alat tersebut mendeteksi ada kartu keamanan yang tergeletak di lantai, maka semua pintu akan terkunci selamanya. Tetapi, setiap ruangan memiliki sebuah kotak yang dapat Anda gunakan untuk menyimpan kartu keamanan sebanyak apapun, yang dapat digunakan nanti.
Jika Anda mencoba memasuki ketiga ruangan langsung dalam sekali jalan, maka setelah Anda memasuki ruang ke 3, Anda telah menggunakan ketiga kartu di tangan Anda, dan Anda akan terjebak di ruangan tersebut selamanya!
Tetapi, jika Anda menggunakan kotak penyimpanan yang ada, maka terdapat kemungkinan untuk meloloskan diri. Sebagai contoh, Anda dapat memasuki ruangan 1 menggunakan kartu pertama di tangan Anda, meletakkan satu buah kartu di kotak penyimpanan, dan menggunakan kartu ketiga untuk kembali ke ruangan mulai (start). Kemudain setelah mengambil tiga buah kartu lagi dari mesin kartu, Anda dapat menggunakan satu buah kartu untuk masuk ke ruangan 1, kemudian mengambil sebuah kartu di kotak penyimpanan beberapa saat yang lalu. Sekarang Anda memiliki tiga kartu lagi dan Anda dapat bergerak melalui tiga buah pintu yang tersisa. Metode ini memungkinkan Anda untuk dapat melalui ketiga ruangan menggunakan sebanyak 6 buah kartu.
Adalah memungkinkan untuk melalui enam buah ruangan menggunakan 123 buah kartu keamanan dengan syarat hanya diperbolehkan membawa maksimal 3 buah kartu.
Misal C adalah jumlah kartu maksimal yang boleh dibawa secara bersamaan.
Misal R adalah banyaknya ruangan yang ingin dilalui.
Misal M(C,R) adalah jumlah minimal kartu yang dibutuhkan dari mesin untuk melalui ruangan dengan banyak R buah ruangan membawa maksimal C buah kartu sekaligus.
Sebagai contoh, M(3,6)=123 dan M(4,6)=23.
Dan, ΣM(C,6)=146 untuk 3 ≤ C ≤ 4.</br>
Diketahui ΣM(C,10)=10382 untuk 3 ≤ C ≤ 10.
Carilah ΣM(C,30) untuk 3 ≤ C ≤ 40.
Answer: 2cd4c0ad8a00c5be99802188ee2628fb
Soal 328
Kita akan mencoba untuk menebak bilangan tersembunyi yang dipilih dari himpunan bilangan bulat {1, 2, ..., n} dengan menanyakan pertanyaan.
Setiap bilangan (pertanyaan) yang kita coba tebak, memiliki harga yang sama dengan nilai bilangan tersebut dan kita akan mendapatkan salah satu dari tiga kemungkinan jawaban :
- "Tebakan Anda lebih rendah dari bilangan yang tersembunyi", atau
- "Ya, itu dia!", atau
- "Tebakan Anda lebih tinggi dari bilangan yang tersembunyi".
Diberikan nilai n, sebuah strategi optimal akan meminimalisir total biaya yang diperlukan (yaitu jumlah semua bilangan yang ditanyakan) bahkan untuk kejadian paling buruk sekalipun.
Jika n=3, cara terbaik yang dapat dilakukan adalah dengan menanyakan bilangan "2". Jawaban dari pertanyaan tersebut akan segera mengantarkan kita untuk menemukan bilangan tersembunyi (dengan total biaya = 2).
Jika n=8, kita dapat memilih untuk menggunakan strategi "binary search": Pertanyaan pertama kita adalah bilangan "4" dan jika bilangan tersembunyi yang ada lebih besar dari 4 kita akan memerlukan dua pertanyaan tambahan.
Misalkan pertanyaan kedua kita adalah "6". Jika bilangan tersembunyi tersebut masih lebih besar dari 6, maka kita perlu pertanyaan ketiga untuk menentukan jawaban antara 7 dan 8.
Kemudian, pertanyaan ketiga kita adalah bilangan "7" dan total biaya untuk kasus terburuk seperti ini akan menjadi 4+6+7=17.
Kita dapat memperbaiki biaya yang diperlukan pada kasus terburuk untuk n=8, dengan menanyakan bilangan "5" sebagai pertanyaan pertama kita.
Jika kita diberitahu bahwa bilangan tersembunyi yang ada adalah lebih besar dari 5, pertanyaan kedua kita akan menjadi "7", kemudian kita akan mengetahui berapakah bilangan tersembunyi yang ada (dengan total biaya sebesar 5+7=12).
Jika kita diberitahu bahwa bilangan tersembunyi yang ada kurang dari 5, maka pertanyaan kedua kita akan menjadi "3" dan jika bilangan tersembunyi yang ada kurang dari 3, pertanyaan ketiga kita akan menjadi "1", dan didapatkan total biaya sebesar 5+3+1=9.
Sejak 12>9, biaya yang diperlukan untuk kasus terburuk mengguanakan strategi ini adalah 12. Hasil ini lebih baik dibandingkan dengan metode sebelumnya, yaitu dengan strategi "binary search"; strategi ini juga lebih baik atau sama dengan strategi lain yang ada.
Sehingga, pada kenyataannya, kita baru saja mendeskripsikan strategi optimal untuk n=8.
Misal C(n) adalah biaya pada kasus terburuk yang diperoleh dengan strategi paling optimal untuk n, seperti yang dijelaskan di atas.
Sehingga C(1) = 0, C(2) = 1, C(3) = 2 dan C(8) = 12.
Dengan cara yang sama, C(100) = 400 dan  C(n) = 17575.
C(n) = 17575.
Carilah  C(n).
C(n).
Answer: 92a3220ad5b17a562c039e6e93d6df90
Soal 329
Susan memiliki seekor katak prima.
Kataknya melompat-lompat di atas 500 buah persegi yang diberi angka dari 1 sampai 500. Ia hanya dapat melompat satu kotak ke sebelah kiri atau ke sebelah kanan, dengan peluang yang sama, dan ia tidak dapat melompat di luar batasan [1;500].
(Jika katak tersebut mendarat di kedua ujungnya, katak tersebut secara otomatis melompat ke kotak yang masih tersedia pada gerakan selanjutnya.)
Saat katak tersebut berada di persegi yang tertulis bilangan prima, ia akan mengeluarkan bunyi ‘P’ (PRIME/PRIMA) dengan peluang 2/3 atau ‘N’ (NOT PRIME/TIDAK PRIMA) dengan peluang 1/3 sebelum ia melompat ke persegi selanjutnya.
Saat ia berada di persegi yang tertulis bilangan bukan prima, ia akan mengeluarkan bunyi ‘P’ dengan peluang 1/3 atau ‘N’ dengan peluang 2/3 sebelum melompat ke persegi selanjutnya.
Diketahui bahwa katak dapat mulai melompat dari persegi manapun dengan peluang yang sama untuk setiap persegi, dan diberikan informasi bahwa Susan akan mendengarkan 15 bunyi pertama dari kataknya, berapakah peluang bahwa Susan akan mendengar barisan PPPPNNPPPNPPNPN?
Berikan jawaban Anda dalam bentuk pecahan p/q yang paling sederhana.
Answer: e392a8b1b053c83e68663e08456bb392
Soal 330
Sebuah barisan tak hingga bilangan real a(n) dinyatakan untuk semua bilangan bulat n sebagai berikut:

Sebagai contoh,
| a(0) = |
|
+ |
|
+ |
|
+ ... = e − 1 |
| a(1) = |
|
+ |
|
+ |
|
+ ... = 2e − 3 |
| a(2) = |
|
+ |
|
+ |
|
+ ... = |
|
e − 6 |
| Dapat ditunjukkan bahwa a(n) sesuai dengan bentuk |
|
untuk A(n) dan B(n) berupa bilangan bulat. |
| Sebagai contoh a(10) = |
|
. |
Carilah A(109) + B(109) dan berikan jawaban Anda yang telah di mod 77 777 777.
Answer: d385d3fe0995b48a782a91477525b154
Soal 331
N×N buah disk diletakkan pada papan permainan berbentuk persegi. setiap disk memiliki sisi hitam dan sisi putih.
Pada setiap langkah, Anda dapat memilih sebuah disk dan membalik semua disk yang terletak pada kolom dan baris yang sama dengan disk ini: sehingga 2×N-1 buah disk telah dibalik. Permainan berakhir saat semua disk menunjukkan sisi berwarna putih. Contoh berikut ini menunjukkan proses permainan pada papan berukuran 5×5.

Dapat dibuktikan bahwa 3 adalah jumlah langkah minimal untuk menyelesaikan permainan ini.
Disk yang terletak di pojok kiri bawah papan berukuran N×N memiliki koordinat (0,0);
disk yang terletak di pojok kanan bawah memiliki koordinat (N-1,0) dan disk di pojok kiri atas memiliki koordinat (0,N-1).
Misal CN adalah susunan disk pada papan dengan N×N buah disk yang memenuhi aturan berikut:
Sebuah disk pada posisi (x,y) memenuhi  , harus menunjukkan sisi hitam; selain itu, disk harus menunjukkan sisi putih. C5 ditunjukkan pada gambar di atas.
, harus menunjukkan sisi hitam; selain itu, disk harus menunjukkan sisi putih. C5 ditunjukkan pada gambar di atas.
Misal T(N) adalah jumlah minimal langkah yang diperlukan untuk menyelesaikan permaian dimulai dari susunan CN atau 0 jika susunan CN tidak dapat diselesaikan.
Kita telah melihat bahwa T(5)=3. Anda juga diberikan informasi bahwa T(10)=29 dan T(1 000)=395253.
Carilah  .
.
Answer: b609ccc578e71db9de0524fff94e1b70
Soal 332
Sebuah segitiga bola adalah gambar yang dibentuk pada permukaan sebuah bola dengan tiga buah busur lingkaran besar yang saling berpotongan membentuk tiga titik.

Misal C(r) adalah bola dengan pusat (0,0,0) dan panjang jari-jari r.
Misal Z(r) adalah himpunan titik-titik pada permukaan C(r) dengan koordinat bilangan bulat.
Misal T(r) adalah himpunan segitiga bola dengan titik-titik yang merupakan anggota Z(r).
Segitiga bola lain, hasil pembentukan dari tiga titik yang berasal dari tiga buah busur lingkaran besar yang sama, adalah tidak di ikut sertakan pada T(r).
Misal A(r) adalah luas wilayah dari segitiga bola terkecil pada T(r).
Sebagai contoh A(14) adalah 3.294040 dibulatkan hingga enam angka di belakang koma.
Carilah  A(r). Berikan jawaban Anda dibulatkan hingga enam angka di belakang koma.
A(r). Berikan jawaban Anda dibulatkan hingga enam angka di belakang koma.
Answer: c2ae53ebfb15db373cfe5d71078ea1ca
Soal 333
Semua bilangan bulat positif dapat dipartisi dengan suatu cara, sehingga setiap suku dari hasil bagi tersebut dapat dinyatakan sebagai 2ix3j, dimana i,j ≥ 0.
Kita hanya akan memperhatikan hasil partisi dimana tidak ada sukunya yang dapat membagi habis suku lain .
Sebagai contoh, partisi dari 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) tidak valid, karena 2 dapat membagi habis 6. Begitu juga partisi 17 = 16 + 1 = (24x30 + 20x30) karena 1 dapat membagi habis 16. Satu-satunya hasil partisi yang sah dari 17 adalah 8 + 9 = (23x30 + 20x32).</br>
Banyak bilangan bulat yang memiliki lebih dari satu partisi yang sah, salah satunya adalah 11 yang memiliki dua hasil partisi.
11 = 2 + 9 = (21x30 + 20x32)
11 = 8 + 3 = (23x30 + 20x31)
Mari kita nyatakan P(n) sebagai banyaknya partisi yang sah dari n. Sebagai contoh, P(11) = 2.
Kita hanya akan memperhatikan bilangan bulat prima q yang memiliki satu buah partisi yang sah, seperti P(17).
Hasil penjumlahan dari bilangan prima q <100 yang memiliki P(q)=1 adalah 233.
Carilah hasil penjumlahan bilangan prima q <1000000 yang memiliki P(q)=1.
Answer: 8408ff3a470a94dbfca1819249eb547d
Soal 334
Di surga Plato, terdapat tak hingga buah mangkuk yang terletak pada satu garis lurus.
Setiap mangkuk dapat berisi beberapa buah kacang polong, atau kosong sama sekali.
Seorang anak kecil memainkan sebuah permaian, yang hanya memperbolehkan satu buah gerakan: mengambil dua kacang polong dari mangkuk manapun, kemudian meletakkan masing-masing satu buah di kedua mangkuk di sebelahnya.
Permainan akan berakhir saat setiap mangkuk berisi antara satu buah kacang polong, atau kosong sama sekali.
Sebagai contoh, terdapat dua buah mangkuk bersebelahan berisi masing-masing 2 dan 3 butir kacang polong, mangkuk lainnya kosong. Delapan langkah berikut ini akan menyelesaikan permainan:

Anda diberikan pola berikut:
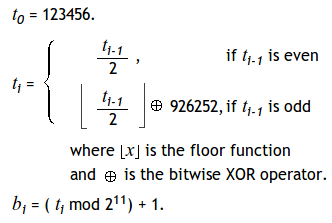
Dua buah suku pertama dari barisan di atas adalah b1 = 289 dan b2 = 145.
Jika kita memulai permainan dengan b1 dan b2 buah kacang polong pada dua mangkok yang bersebelahan, 3419100 gerakan akan diperlukan untuk menyelesaikan permaian.
Sekarang terdapat 1500 mangkuk bersebelahan yang masing-masing berisi b1, b2,..., b1500 buah kacang polong secara berurutan, mangkuk lainnya kosong. Carilah berapa banyak gerakan yang diperlukan supaya permainan dapat berakhir.
Answer: 71851da3058acf6b74e90251bdf4aa8f
Soal 335
Saat Peter merasa bosan, ia meletakkan beberapa mangkuk, berisi satu buah kacang polong pada tiap mangkuknya, disusun membentuk suatu lingkaran. Setelah ini, ia mengambil semua kacang polong dari satu mangkuk, dan meletakkannya satu persatu pada mangkuk di sebelahnya searah jarum jam. Ia mengulang proses ini lagi, dimulai dari mangkuk dimana ia menjatuhkan kacang polong terakhir, sampai kondisi mula-mula muncuk kembali. Sebagai contoh, dengan 5 mangkuk, ia melakukan tindakan berikut:

Sehingga dengan 5 buah mangkuk, Peter memerlukan 15 gerakan untuk mengembalikan kondisi mangkuk ke kondisi mula-mula.
Misal M(x) menyatakan banyaknya gerakan yang diperlukan agar mangkuk-mangkuk dapat kembali ke kondisi awal, dimulai dengan x buah mangkuk. Maka, M(5) = 15. Dapat juga dibuktikan bahwa M(100) = 10920.
Carilah  M(2k+1). Berikan jawaban Anda yang telah di modulo 79.
M(2k+1). Berikan jawaban Anda yang telah di modulo 79.
Answer: 9a519cfa0ebdd4d1dd318f14b5799eea
Soal 336
Sebuah kereta digunakan untuk mengantarkan empat gerbong dengan urutan: ABCD. Tetapi, terkadang saat kereta tiba untuk mengambil gerbon, gerbong-gerbong tersebut tidak diletakkan pada urutan yang benar.
Untuk mengatur ulang urutan gerbong, semua gerbong di dorong ke sebuah alat pemutar besar. Setelah gerbong yang ingin diputar dilepas dari gerbong lainnya, kemudian kereta menjauh dari alat pemutar, menarik gerbong lain yang masih menempel padanya. Kemudian gerbong yang ingin diperbaiki posisinya diputar 180 derajat. Kemudian semua gerbong kembali di satukan, dan proses ini dilakukan berulang-ulang namun diupayakan supaya didapatkan jumlah penggunaan alat pemutar sesedikit mungkin.
Beberapa susunan, seperti ADCB, dapat diselesaikan dengan mudah: gerbong A dan D dipisah, dan setelah DCB diputar, maka susunan yang benar telah didapatkan.
Tetapi, Simple Simon, seorang masinis kereta, tidak memahami prinsip efisiensi, sehingga ia selalu menyelesaikan permasalahan ini dengan menempatkan gerbong A pada posisi yang benar, kemudian gerbong B, dan seterusnya.
Menggunakan empat buah gerbong, susunan gerbong terburuk yang mungkin dialami Simon, dimana kita akan menyebut susunan tersebut susunan maximix, adalah DACB dan DBAC; setiap gerbong memerlukan lima rotasi (bahkan walaupun menggunakan cara yang paling efisien, cara tersebut masih membutuhkan tiga rotasi). Proses yang Simon gunakan untuk memperbaiki posisi gerbong DACB ditunjukkan pada gambar berikut.

Dapat dibuktikan bahwa terdapat 24 susunan maximix untuk enam buah gerbong, dimana susunan maximix ke sepuluh adalah DFAECB.
Carilah susunan maximix ke 2011 untuk sebelas buah gerbong.
Answer: 7968e48fc692ce25bf7f5494f4ab6814
Soal 337
Misal {a1, a2,..., an} adalah barisan bilangan bulat dengan panjang n dengan aturan:
- a1 = 6
- untuk semua 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+1 1
Misal S(N) adalah banyaknya barisan dengan an ≤ N.
Sebagai contoh, S(10) = 4: {6}, {6, 8}, {6, 8, 9} dan {6, 10}.
Dapat dibuktikan bahwa S(100) = 482073668 dan S(10 000) mod 108 = 73808307.
Carilah S(20 000 000) mod 108.
1 φ adalah fungsi totient Euler.
Answer: a60bbbe1b90254043fb92820492a2f96
Soal 338
Sebuah kertas kotak-kotak berbentuk persegi panjang dengan ukuran berupa bilangan bulat w × h diberikan. Ukuran kotak-kotaknya adalah 1.
Saat kita memotong kertas tersebut menjadi dua bagian mengikuti garis pada kotak-kotak, dan kemudian menysun potongan kertas tersebut tanpa tertumpuk satu sama lain, kita dapat membuat persegi panjang baru dengan ukuran yang berbeda.
Sebagai contoh, dari kertas berukuran 9 × 4 , kita dapat membuat persegi panjang dengan ukuran 18 × 2, 12 × 3 dan 6 × 6 dengan memotong dan menyusun kertas dengan cara berikut:

Dengan cara yang sama, dari kertas berukuran 9 × 8 , kita dapat membuat persegi panjang dengan ukuran 18 × 4 dan 12 × 6 .
Untuk sepasang w dan h, kita misalkan F(w,h) adalah banyaknya persegi panjang berbeda yang dapat dibuat dari sebuah kertas dengan ukuran w × h .
Sebagai contoh, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2.
Perlu diingat bahwa persegi panjang yang kongruen dengan ukuran awal kertas tidak ikut dihitung pada F(w,h).
Perlu diingat juga bahwa persegi panjang dengan ukuran w × h dan h × w tidak dianggap berbeda.
Untuk sebuah bilangan bulat N, misal G(N) adalah hasil penjumlahan dari semua F(w,h) untuk semua pasangan w dan h yang memenuhi 0 < h ≤ w ≤ N.
Kita dapat membuktikan bahwa G(10) = 55, G(103) = 971745 dan G(105) = 9992617687.
Carilah G(1012). Berikan jawaban Anda yang telah di modulo 108.
Answer: 99f4f702713f3422ced01dd7d3d79644
Soal 339
"Dan ia (Peredur) kemudian datang menuju sebuah lembah, dimana di sana mengalir sebuah sungai; dan sekeliling lembah tersebut ditutupi pohon-pohon, dan di kedua sisi dari sungai terdapat padang rumput. Di salah satu sisi dari sungai ia melihat kawanan domba putih, dan pada sisi yang satunya lagi kawanan domba hitam. Dan apabila salah satu dari domba putih berteriak menangis, satu dari domba hitam akan menyebrang dan menjadi putih; dan apabila salah satu dari domba hitam berteriak menangis, satu dari domba putih akan menyebrang dan menjadi hitam."
<a href=http://en.wikisource.org/wiki/The_Mabinogion/Peredur_the_Son_of_Evrawc>en.wikisource.org</A>
Pada mulanya, pada setiap kawanan terdapat n ekor domba. Setiap domba (apapun warnanya) memiliki peluang yang sama untuk menangis. Setelah seekor kambing menangis dan seekor kambing dari kawanan warna lain menyebrang, maka Peredur dapat mengambil beberapa ekor domba putih dengan tujuan untuk memaksimalkan nilai harapan (expected value) dari banyak akhir domba hitam. E(n) adalah nilai harapan (expected value) dari jumlah domba hitam terakhir apabila Peredur menggunakan strategi optimal.
Anda diberikan informasi bahwa E(5) = 6.871346 dibulatkan hingga 6 angka di belakang koma.
Carilah E(10 000) dan berikan jawaban Anda dibulatkan hingga 6 angka di belakang koma.
Answer: 0be02210b2d2212d37d026478093c457
Soal 340
Untuk bilangan bulat tetap a, b, c, dinyatakan sebuah fungsi gila F(n) sebagai berikut:
F(n) = n - c untuk semua n > b
F(n) = F(a + F(a + F(a + F(a + n)))) untuk semua n ≤ b.
Juga, dinyatakan S(a, b, c) =  .
.
Sebagai contoh, jika a = 50, b = 2000 dan c = 40, maka F(0) = 3240 dan F(2000) = 2040.
Juga, S(50, 2000, 40) = 5204240.
Carilah 9 digit terakhir dari S(217, 721, 127).
Answer: fc838afe9ecde39bbe230923d7b50775
Soal 341
Sebuah Barisan self-describing Golomb {G(n)} adalah satu-satunya barisan tidak turun yang berisi bilangan asli n yang muncul persis G(n) kali di barisan tersebut. Nilai dari G(n) untuk n bilangan pertama adalah
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| G(n) | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | … |
Anda diberikan informasi bahwa G(103) = 86, G(106) = 6137.
Anda juga diberikan informasi bahwa ΣG(n3) = 153506976 for 1 ≤ n < 103.
Carilah ΣG(n3) for 1 ≤ n < 106.
Answer: 7c163c3b4886943667b5c89db0a6cd02
Soal 342
Perhatikan bilangan 50.
502 = 2500 = 22 × 54, so φ(2500) = 2 × 4 × 53 = 8 × 53 = 23 × 53. 1
Sehingga 2500 adalah bilangan kuadrat dan φ(2500) adalah bilangan kubik.
Carilah hasil penjumlahan dari semua bilangan n, 1 < n < 1010 sehingga φ(n2) adalah bilangan kubik.
1 φ menyatakan Fungsi Totient Euler.
Answer: 0e9add0383d4116c7c5cb3dc73fc0536
Soal 343
Untuk setiap bilangan bulat positif k, sebuah barisan terhingga ai yang berisi pecahan xi/yi dinyatakan dengan:
a1 = 1/k dan
ai = (xi-1+1)/(yi-1-1) dijadikan ke bentuk paling sederhana untuk i>1.
Saat ai mencapai bilangan bulat n, barisan akan berhenti. (Yaitu, saat yi=1.)
Dinyatakan f(k) = n.
Sebagai contoh, untuk k = 20:
1/20 → 2/19 → 3/18 = 1/6 → 2/5 → 3/4 → 4/3 → 5/2 → 6/1 = 6
Sehingga f(20) = 6.
Juga f(1) = 1, f(2) = 2, f(3) = 1 dan Σf(k3) = 118937 untuk 1 ≤ k ≤ 100.
Carilah Σf(k3) untuk 1 ≤ k ≤ 2×106.
Answer: 0e10bd111425ad8e1343ac79dac7bb0e
Soal 344
Salah satu variasi dari permainan dolar perak N.G. de Bruijn memiliki penjelasan sebagai berikut:
Pada potongan kertas memiliki banyak persegi, beberapa buah koin diletakkan, satu buah koin untuk setiap persegi. Namun hanya ada satu koin, yang disebut sebagai dolar perak, yang mempunyai nilai tertentu. Dua pemain memainkan permainan secara bergiliran. Pada setiap giliran seorang pemain diwajibkan untuk melakukan gerakan reguler atau sebuah gerakan spesial.
Sebuah gerakan reguler dilakukan dengan memilih satu buah koin, dan memindahkannya ke satu atau lebih persegi di sebelah kiri. Koin tidak dapat keluar dari kertas atau melompati koin lainnya.
Alternatif lain, seorang pemain dapat memilih untuk melakukan gerakan spesial, yaitu mengambil koin yang ada di paling kiri. Jika tidak ada gerakan reguler lagi yang bisa dilakukan, pemain harus mengambil koin yang ada di paling kiri.
Pemenangnya adalah pemain yang mengambil dolar perak.

Sebuah susunan kemenangan adalah susunan dari koin-koin pada kertas dimana pemain pertama pasti akan menang, tidak peduli apapun yang dilakukan oleh pemain kedua.
Misal W(n,c) adalah banyaknya susunan kemenangan untuk sepotong kertas dengan n buah persegi, c buah koin yang tidak berarti dan sebuah dolar perak.
Anda diberikan informasi bahwa W(10,2) = 324 dan W(100,10) = 1514704946113500.
Carilah W(1 000 000, 100) modulo bilangan semiprima 1000 036 000 099 (= 1 000 003 · 1 000 033).
Answer: 38e7b980b38fcac89b3e267e328cd292
Soal 345
Kita nyatakan Jumlah Matriks dari suatu matriks sebagai hasil penjumlahan terbesar dari elemen-elemen matriks, dengan syarat hanya terdapat satu elemen yang dipilih di setiap baris dan kolomnya. Sebagai contoh, Jumlah Matriks dari matriks berikut ini sama dengan 3315 ( = 863 + 383 + 343 + 959 + 767):
7 53 183 439 863
497 383 563 79 973
287 63 343 169 583
627 343 773 959 943
767 473 103 699 303
Carilah Jumlah Matriks dari:
7 53 183 439 863 497 383 563 79 973 287 63 343 169 583
627 343 773 959 943 767 473 103 699 303 957 703 583 639 913
447 283 463 29 23 487 463 993 119 883 327 493 423 159 743
217 623 3 399 853 407 103 983 89 463 290 516 212 462 350
960 376 682 962 300 780 486 502 912 800 250 346 172 812 350
870 456 192 162 593 473 915 45 989 873 823 965 425 329 803
973 965 905 919 133 673 665 235 509 613 673 815 165 992 326
322 148 972 962 286 255 941 541 265 323 925 281 601 95 973
445 721 11 525 473 65 511 164 138 672 18 428 154 448 848
414 456 310 312 798 104 566 520 302 248 694 976 430 392 198
184 829 373 181 631 101 969 613 840 740 778 458 284 760 390
821 461 843 513 17 901 711 993 293 157 274 94 192 156 574
34 124 4 878 450 476 712 914 838 669 875 299 823 329 699
815 559 813 459 522 788 168 586 966 232 308 833 251 631 107
813 883 451 509 615 77 281 613 459 205 380 274 302 35 805
Answer: cf3b784c8593890043b17e24088125d4
Soal 346
Bilangan 7 adalah sebuah bilangan yang spesial, karena 7 adalah 111 jika di tulis di basis 2, dan 11 jika ditulis di basis 6
(i.e. 710 = 116 = 1112). Atau dengan kata lain, 7 adalah sebuah bilangan berulang pada setidaknya dua buah basis b > 1.
Kita akan menyebut bilangan bulat positif yang memiliki sifat ini sebagai bilangan berulang kuat. Dapat dibuktikan bahwa terdapat 8 buah bilangan berulang kuat kurang dari 50: {1,7,13,15,21,31,40,43}.
Lebih lanjut lagi, hasil penjumlahan dari semua bilangan berulang kuat kurang dari 1000 sama dengan 15864.
Carilah jumlah dari semua bilangan berulang kuat kurang dari 1012.
Answer: a17874b5a9ec9d7fc8c6489ab8ff29b9
Soal 347
Bilangan bulat terbesar ≤ 100 yang habis dibagi hanya oleh bilangan prima 2 dan 3 adalah 96, karena 96=32*3=25*3. Untuk dua bilangan prima berbeda p dan q, kita misalkan M(p,q,N) adalah bilangan bulat positif terbesar ≤N yang hanya habis dibagi oleh bilangan prima p dan q, dan M(p,q,N)=0 jika tidak ada bilangan bulat positif yang memenuhi sifat di atas.
Sebagai contoh M(2,3,100)=96.
M(3,5,100)=75 dan bukan 90, karena 90 habis dibagi oleh 2 ,3 dan 5.
Juga M(2,73,100)=0 karena tidak terdapat bilangan bulat positif ≤ 100 yang habis dibagi oleh 2 dan 73.
Misal S(N) adalah hasil penjumlahan semua hasil M(p,q,N) berbeda. S(100)=2262.
Carilah S(10 000 000).
Answer: 96ce0eabcbe7a2b2eb1197a1bcc5d37b
Soal 348
Banyak bilangan dapat dituliskan sebagai hasil penjumlahan dari sebuah bilangan kuadrat dan sebuah bilangan kubik. Beberapa dari mereka dapat dituliskan dengan leibh dari satu cara.
Perhatikan bahwa terdapat suatu bilangan palindrom yang juga dapat dituliskan sebagai hasil penjumlahan dari sebuah bilangan kuadrat dan sebuah bilangan kubik, yang kedua bilangan tersebut lebih besar dari 1, dengan persis 4 buah cara.
Sebagai contoh, 5229225 adalah sebuah bilangan palindrom, dan dapat dituliskan persis dengan 4 buah cara berbeda:
22852 + 203
22232 + 663
18102 + 1253
11972 + 1563
Carilah hasil penjumlahan dari lima buah bilangan palindrom terkecil yang memiliki sifat seperti di atas.
Answer: f286f9159fc20aeb97a8bf8396ba64de
Soal 349
Seekor semut bergerak di suatu kotak-kotak persegi yang diwarnai hitam atau putih.
Semut tersebutr selalu menghadap ke salah satu dari arah-arah utama (kiri, kanan, atas atau bawah) dan bergerak dari satu persegi ke persegi lain yang bersebelahan sesuai dengan aturan berikut:
- jika semut tersebut berada pada persegi hitam, maka ia akan mengganti warna persegi tersebut menjadi putih, berputar 90 derajat berlawanan arah jarum jam, dan bergerak maju satu kotak.
- jika semut tersebut berada pada persegi putih, maka ia akan mengganti warna persegi tersebut menjadi hitam, berputar 90 derajat searah jarum jam, dan bergerak maju satu langkah.
Dimulai dengan daerah kotak-kotak yang semuanya bewarna putih, berapa banyak persegi yang bewarna hitam setelah 1018 langkah dari semut tersebut?
Answer: 412b0faec10b3adb415363d2df26530d
Soal 350
Sebuah daftar dengan ukuran n adalah barisan n buah bilangan asli.
Contohnya adalah (2,4,6), (2,6,4), (10,6,15,6), dan (11).
Faktor persekutuan terbesar (greatest common divisor), atau gcd dari suatu daftar adalah bilangan asli terbesar yang dapat membagi semua bilangan pada daftar.
Examples: gcd(2,6,4) = 2, gcd(10,6,15,6) = 1 dan gcd(11) = 11.
Kelipatan persekutuan terkecil (least common multiple), atau lcm dari suatu daftar adalah bilangan asli terkecil yang dapat habis dibagi oleh semua bilangan pada daftar.
Examples: lcm(2,6,4) = 12, lcm(10,6,15,6) = 30 dan lcm(11) = 11.
Misal f(G, L, N) adalah banyaknya daftar dengan ukuran N yang memiliki gcd ≥ G dan lcm ≤ L. Sebagai contoh:
f(10, 100, 1) = 91.
f(10, 100, 2) = 327.
f(10, 100, 3) = 1135.
f(10, 100, 1000) mod 1014 = 3286053.
Carilah f(106, 1012, 1018) mod 1014.
Answer: cad3ce6a252568bbcb41ca627d7e58ae
Soal 351
Sebuah taman segi enam dengan orde n dibentuk dari kumpulan titik-titik yang dapat membentuk segitiga-segitiga kecil yang berada di dalam segi enam dengan panjang sisi n. Berikut in adalah sebuah contoh dari taman segi enam dengan orde 5:

Titik yang diberi tanda hijau adalah titik yang tidak dapat terlihat dari titik tengah, karena terhalang oleh titik lain yang lebih dekat dengan titik tengah. Dapat kita lihat bahwa untuk taman segi enam denagn orde 5, 30 titik tidak dapat terlihat dari titik tengah.
Misalkan H(n) adalah banyaknya titik yang tersembunyi dari titik tengah taman segi enam dengan orde n.
H(5) = 30. H(10) = 138. H(1 000) = 1177848.
Carilah H(100 000 000).
Answer: 338481092e945257756075a8d03978fd
Soal 352
Setiap satu dari 25 domba pada suatu kawanan harus di uji dari suatu virus langka, yang diketahui menginfeksi 2% dari populasi domba. Sebuah metode test PCR yang akurat dan sangat sensitif dapat dilakukan kepada sampel darah, yang dapat mengeluarkan hasil tes positif / negatif dengan jelas, namun proses ini sangat memakan waktu dan mahal.
Karena harga yang tinggi, sang dokter hewan yang sedang bertugas menyarankan dibanding melakukan 25 tes terpisah, kita dapat menggunakan prosedur berikut:
Domba-domba dibagi menjadi 5 kelompok berisi 5 domba di setiap kelompok.
Untuk setiap kelompok, 5 sampel darah dicampur bersama, kemudian sebuah tes dilakukan. Kemudian,
- Jika hasil tes adalah negatif, maka semua domba di kelompok tersebut dipastikan bebas virus.
- Jika hasil tes adalah positif, 5 tes tambahan akan dilakukan (tes terpisah untuk setiap ekor domba) untuk menentukan domba mana yang terkena virus.
Semenjak peluang seekor hewan terkena virus sangat spesifik, yaitu hanya 0.02, tes pertama (pada sampel darah yang dikumpulkan) pada setiap kelompoknya akan menjadi:
- Negatif (dan tidak ada lagi tes yang perlu dilakukan) dengan peluang 0.985 = 0.9039207968.
- Positif (5 tes tambahan perlu dilakukan) dengan peluang 1 - 0.9039207968 = 0.0960792032.
Sehingga, nilai perkiraan (expected number) dari hasil tes untuk setiap kelompok adalah 1 + 0.0960792032 × 5 = 1.480396016.
Dampaknya, kelima kelompok dapat diperiksa menggunakan rata-rata hanya 1.480396016 × 5 = 7.40198008 kali tes, dimana hasil tersebut menggambarkan penghematan besar, yaitu lebih dari 70% !
Walaupun metode yang baru saja dijelaskan terlihat sangat efisien, metode tersebut masih bisa sangat disempurnakan (selalu asumsikan bahwa hasil test cukup sensitif, dan tidak ada efek merugikan yang dihasilkan oleh pencampuran sampel darah). Sebagai contoh:
- Kita dapat memulai dengan mencampurkan ke-25 sampel darah dan melakukan tes pada campuran tersebut. Dapat dibuktikan bahwa terdapat sekitar 60.35% kemungkinan tes ini akan mengeluarkan hasil negatif, sehingga tidak perlu lagi ada tes dibutuhkan. Tes selanjutnya hanya diperlukan oleh 39.65% kemungkinan lainnya.
- Jika kita mengetahui informasi setidaknya satu ekor hewan dalam setiap kelompok berisi 5 ekor hewan terinfeksi, dan hasil tes 4 ekor hewan pertama mengeluarkan hasil negatif, kita tidak lagi perlu melakukan tes untuk hewan ke lima (kita tahu bahwa hewan tersebut pasti terinfeksi).
- Kita dapat mencoba mengelompokkan domba dengan banyak kelompok yang berbeda / banyak hewan yang berbeda di setiap kelompoknya, menyesuaikan angka-angka tersebut pada setiap level tes sehingga jumlah nilai perkiraan percobaan (expected number) dari tes akan berkurang.
Untuk menyederhanakan berbagai macam kemungkinan yang ada, terdapat satu syarat yang harus kita ikuti saat menentukan skema tes yang paling efisien: Saat kita memulai dengan sampel darah campuran, semua domba yang darahnya ikut masuk dalam sampel tersebut harus sepenuhnya diperiksa (sehingga kesimpulan terinfeksi / bebas virus harus dimiliki oleh semua domba) sebelum kita meneliti hewan lainnya.
Untuk contoh ini, terlihat bahwa skema tes yang biayanya paling efisien (kita akan menyebut ini sebagai strategi optimal) membutuhkan rata-rata hanya 4.155452 kali tes!
Menggunakan strategi optimal, misal T(s,p) menyatakan rata-rata jumlah tes yang diperlukan untuk mengetahui kondisi kawanan berisi s ekor domba, dengan kemungkinan terkena virus p untuk setiap ekor domba.
Sehingga, jika dibulatkan hingga enam angka di belakang koma, T(25, 0.02) = 4.155452 dan T(25, 0.10) = 12.702124.
Carilah ΣT(10000, p) untuk p=0.01, 0.02, 0.03, ... 0.50.
Berikan jawaban Anda yang dibulatkan hingga enam angka di belakang koma.
Answer: 2e74b2fb574d6318cdbf2a41ad006de7
Soal 353
Sebuah bulan dapat digambarkan dengan bola C(r) yang berpusat di (0,0,0) dan memiliki panjang jari-jari r.
Terdapat stasiun di bulan pada suatu titik di permukaan C(r) yang memiliki koordinat berupa bilangan bulat. Stasiun pada (0,0,r) disebut sebagai stasiun Kutub Utara, stasiun pada (0,0,-r) disebut stasiun Kutub Selatan.
Semua stasiun dihubungkan satu sama lain melalui jalan terpendek pada permukaan bulan melalui stasiun-stasiun lain. Sebuah perjalanan antara dua stasiun adalah beresiko. Jika d adalah panjang jalan antara dua stasiun, (d/(π r))2 adalah tingkat resiko dari perjalanan (mari kita sebut ini sebagai resiko perjalanan). Jika perjalanan melibatkan lebih dari dua stasiun, resiko perjalanan didapat dari hasil penjumlahan resiko pada jalan-jalan yang digunakan.
Perjalanan langsung dari stasiun Kutub Utara ke stasiun Kutub Selatan memiliki jarak πr dan resiko 1. Perjalanan dari stasiun Kutub Utara ke stasiun Kutub Selatan melalui (0,r,0) memiliki panjang yang sama, namun resiko yang elbih kecil: (½πr/(πr))2+(½πr/(πr))2=0.5.
Resiko terkecil perjalanan dari stasiun Kutub Utara ke stasiun Kutub Selatan pada C(r) adalah M(r).
Anda diberikan informasi bahwa M(7)=0.1784943998 dibulatkan hingga 10 angka di belakang koma.
Carilah ∑M(2n-1) untuk 1≤n≤15.
Berikan jawaban Anda dibulatkan hingga 10 angka di belakang koma dengan format a.bcdefghijk.
Answer: 211b5626459be71baefc78478d18bdc3
Soal 354
Misalkan terdapat sarang madu dari lebah madu, dimana setiap sel adalah sebuah segi enam sempurna dengan panjang sisi 1.

Satu buah sel ditempati oleh ratu lebah.
Untuk bilangan real positif L, misal B(L) adalah banyaknya sel yang dilalui dengan jarak L dari sel yang ditempati ratu lebah (semua jarak diukur dari pusat ke pusat); Anda dapat mengasumsikan sarang madu yang ada cukup besar untuk mengakomodasi jarak berapapun yang ingin kita hitung.
Sebagai contoh, B(√3) = 6, B(√21) = 12 dan B(111 111 111) = 54.
Carilah banyaknya L ≤ 5·1011 yang menghasilkan B(L) = 450.
Answer: e36240897614dc46e83405ae8cdf198c
Soal 355
Dinyatakan Co(n) sebagai hasil penjumlahan maksimal yang mungkin dari himpunan bagian yang elemen-elemennya saling koprima dari {1, 2, ..., n}.
Sebagai contoh Co(10) adalah 30 dan mencapai maksimum pada himpunan bagian {1, 5, 7, 8, 9}.
Anda diberikan informasi bahwa Co(30) = 193 dan Co(100) = 1356.
Carilah Co(200000).
Answer: 41cb97b6d02878d79f8b2e3b6c74920a
Soal 356
Misal an adalah akar real terbesar dari sebuah polinomial g(x) = x3 - 2n·x2 + n.
Sebagai contoh, a2 = 3.86619826...
Carilah delapan digit terakhir dari  .
.
Catatan:  menyatakan fungsi pembulatan ke bawah.
menyatakan fungsi pembulatan ke bawah.
Answer: ab2104e80fa7da630ce7fd835d8006ee
Soal 357
Perhatikan faktor-faktor dari 30: 1,2,3,5,6,10,15,30.
Dapat terlihat bahwa untuk setiap faktor d dari 30, d+30/d adalah bilangan prima.
Carilah hasil penjumlahan semua bilangan bulat positif n yang tidak melebihi 100 000 000
sehingga
untuk setiap faktor d dari n, d+n/d adalah bilangan prima.
Answer: ed25b13b18a21c1077fed00ef42f503b
Soal 358
Sebuah bilangan siklik dengan n buah digit memiliki sifat yang menarik:
Saat bilangan tersebut dikalikan dengan 1, 2, 3, 4, ... n, semua hasil kalinya memiliki digit-digit yang sama, dengan urutan yang sama, namun perlu dirotasi memutar!
Bilangan siklik 6 digit terkecil 142857 :
142857 × 1 = 142857
142857 × 2 = 285714
142857 × 3 = 428571
142857 × 4 = 571428
142857 × 5 = 714285
142857 × 6 = 857142
Bilangan siklik selanjutnya adalah 0588235294117647 dengan 16 buah digit :
0588235294117647 × 1 = 0588235294117647
0588235294117647 × 2 = 1176470588235294
0588235294117647 × 3 = 1764705882352941
...
0588235294117647 × 16 = 9411764705882352
Perlu diingat bahwa untuk bilangan siklik, angka nol di depan adalah penting.
Hanya terdapat satu buah bilangan siklik, dimana sebelas digit paling kirinya adalah 00000000137 dan lima digit paling kanannya adalah 56789 (sehingga, bilangan ini mempunyai bentuk 00000000137...56789 dengan bilangan yang tidak diketahui di tengahnya). Carilah hasil penjumlahan darn semua digit-digitnya.
Answer: 359e1ec8aeaa3932b54f2a5d20fa4f73
Soal 359
Sebanyak tak terhingga orang (diberi nomor 1, 2, 3, dst.) berbaris untuk mendapatkan kamar di hotel tak terhingga terbaru Hilbert. Hotel tersebut terdiri dari tak terhingga lantai (diberi nomor 1, 2, 3, dst.), dan pada setiap lantai terdapat tak terhingga buah kamar (diberi nomor 1, 2, 3, dst.).
Mula-mulanya hotel tersebut masih kosong. Hilbert menyatakan sebuah peraturan tentang bagaimana orang ke-n bisa mendapatkan sebuah kamar: orang ke-n akan mendapatkan kamar kosong pertama di lantai terbawah dengan memenuhi salah satu kondisi berikut ini:
- kamar di lantai tersebut kosong
- kamar di lantai tersebut tidak kosong, dan jika orang terakhir yang mengambil kamar di lantai tersebut adalah orang ke-m, maka m + n haruslah bilangan kuadrat sempurna
Orang ke-1 mendapatkan kamar 1 di lantai 1 karena lantai 1 masih kosong.
Orang ke-2 tidak mendapatkan kamar 2 di lantai 1 karena 1 + 2 = 3 bukanlah kuadrat sempurna.
Orang ke-2 malah mendapatkan kamar 1 di lantai 2 karena lantai 2 masih kosong.
Orang ke-3 mendapatkan kamar 2 di lantai 1 karena 1 + 3 = 4 adalah bilangan kuadrat.
Dan pada akhirnya, setiap orang di antrian akan mendapatkan sebuah kamar di hotel.
Dinyatakan P(f, r) adalah n apabila orang ke-n menempati ruang r pada lantai f, dan 0 jika tidak ada orang yang menempati ruangan tersebut. Berikut ini adalah beberapa contohnya:
P(1, 1) = 1
P(1, 2) = 3
P(2, 1) = 2
P(10, 20) = 440
P(25, 75) = 4863
P(99, 100) = 19454
Carilah hasil penjumlahan dari semua P(f, r) untuk semua bilangan positif f dan r sehingga f × r = 71328803586048 dan berikan 8 digit terakhir dari jawaban Anda.
Answer: 91525a22396940a99c496efcb75f2eee
Soal 360
Diberikan dua titik (x1,y1,z1) dan (x2,y2,z2) pada ruang tiga dimensi, jarak Manhattan antara kedua titik tersebut dinyatakan dengan
|x1-x2|+|y1-y2|+|z1-z2|.
Misal C(r) adalah bola dengan panjang jari-jari r dan berpusat di titik origin O(0,0,0).
Misal I(r) adalah himpunan dari semua titik-titk yang memiliki koordinat bilangan bulat pada permukaan C(r).
Misal S(r) adalah hasil penjumlahan jarak Manhattan dari semua elemen dari I(r) dengan titik origin O.
Sehingga S(45)=34518.
Carilah S(1010).
Answer: 82ec91527315eafb7e3acc139eeeb8eb
Soal 361
Barisan Thue-Morse {Tn} adalah sebuah barisan biner yang memenuhi:
- T0 = 0
- T2n = Tn
- T2n+1 = 1 - Tn
Beberapa suku pertama dari {Tn} adalah sebagai berikut:
01101001100101101001011001101001....
Kita akan menyatakan {An} sebagai barisan bilangan bulat berurutan yang didapat dari ekspresi biner dari setiap elemen yang muncul dari sub barisan di {Tn}.
Sebagai contoh, bilangan desimal 18 dapat dinyatakan sebagai 10010 di dalam bilangan biner. 10010 muncul di {Tn} (T8 hingga T12), sehingga 18 adalah elemen dari {An}.
Bilangan desimal 14 dituliskan sebagai 1110 dalam biner. 1110 tidak pernah muncul di {Tn}, sehingga 14 bukanlah elemen dari {An}.
Beberapa suku pertama dari An adalah sebagai berikut:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | … |
| An | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 10 | 11 | 12 | 13 | 18 | … |
Kita juga dapat membuktikan bahwa A100 = 3251 dan A1000 = 80852364498.
Carilah 9 digit terakhir dari  .
.
Answer: 6540278145900f1fa45b95cc2f9599f1
Soal 362
Perhatikan bilangan 54.
54 dapat difaktorkan dengan 7 cara berbeda menjadi satu atau lebih faktor yang lebih besar dari 1:
54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9 dan 2×3×3×3.
Jika kita mengumpulkan faktor-faktor yang merupakan bilangan bukan kuadrat, maka hanya dua cara yang tersisa: 3×3×6 dan 2×3×3×3.
Kita akan menyebut Fsf(n) sebagai banyaknya cara bilangan n dapat difaktorkan menggunakan faktor-faktor bukan kuadrat yang lebih besar dari 1, sehingga Fsf(54)=2.
Misal S(n) adalah ∑Fsf(k) untuk k=2 sampai n.
S(100)=193.
Carilah S(10 000 000 000).
Answer: b62f0d524bec8653ba7b8a2cab70260b
Soal 363
Sebuah kurva Bézier kubik dibentuk dengan empat titik: P0, P1, P2 dan P3.

Kurva dibangun dengan cara sebagai berikut:
Pada segmen garis P0P1, P1P2 dan P2P3 titik Q0,Q1 dan Q2 digambarkan sehingga
P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t pada [0,1]).
Pada segmen garis Q0Q1 dan Q1Q2 titik R0 dan R1 digambarkan sehingga
Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t untuk nilai t yang sama.
Pada segmen garis R0R1 titik B digambarkan sehingga that R0B / R0R1 = t untuk nilai t yang sama.
Kurva Bézier yang dinyatakan oleh titik P0, P1, P2, P3 adalah tempat kedudukan (locus) dari titik B saat Q0 menempati semua posisi yang mungkin dari segmen P0P1.
(Mohon diingat bahwa untuk semua titik, nilai t adalah sama.)
Di alamat website (eksternal) ini Anda akan menemukan applet yang akan menggambarkan cara untuk menggambari titik P0, P1, P2 dan P3 untuk melihat bagaimana cara menggambarkan kurva Bézier (kurva hijau) yang dibentuk dari titik-titik tersebut. Anda juga dapat menggeser titik Q0 sepanjang segmen P0P1.
Dari hasil penggambaran tersebut jelas bahwa kurva Bézier adalah persinggungan segmen P0P1 di P0 dan P2P3 pada P3.
Sebuah kuva Bézier kubik dengan P0=(1,0), P1=(1,v), P2=(v,1) dan P3=(0,1) digunakan untuk memperkirakan seperempat lingkaran.
Nilai v</var> > 0 dipilih sehingga luas yang dibatasi oleh garis OP0, OP3 dan kurva sama dengan π/4 (luas seperempat lingkaran).
| Yaitu, jika L adalah panjang kurva, hitunglah 100 × | L − π/2 π/2 |
Answer: 2bc63386b7cccc64c67f90e719936143
Soal 364
Terdapat N buah bangku pada satu baris. Kemudian akan ada N orang yang datang untuk mengisi bangku-bangku tersebut dengan aturan sebagai berikut:
- Jika terdapat sebuah bangku yang kedua bangku di sebelahnya kosong, maka bangku tersebut akan ditempati.
- Jika tidak terdapat bangku seperti itu, dan hanya terdapat bangku yang hanya salah satu sebelahnya yang diisi, maka bangku teresbut akan ditempati.
- Jika tidak, hanya terdapat pilihan untuk menempati bangku yang masih tersisa.
Gambar berikut ini menunjukkan T(4)=8.

Kita dapat membuktikan bahwa T(10) = 61632 dan T(1 000) mod 100 000 007 = 47255094.
Carilah T(1 000 000) mod 100 000 007.
Answer: d631977573d415a4766de9e6bd388cca
Soal 365
Koefisien binomial C(1018,109) adalah sebuah bilangan dengan lebih dari 9 milyar (9×109) digit.
Misal M(n,k,m) menyatakan koefisien binomial C(n,k) modulo m.
Hitunglah ∑M(1018,109,p*q*r) untuk 1000<p<q<r<5000 dan p,q,r merupakan bilangan prima.
Answer: 53addf69042b0cefbeb94f3bd3224918
Soal 366
Dua orang pemain, Anton dan Bernhard, sedang memainkan permainan berikut.
Terdapat satu tumpukan berisi n buah batu.
Pemain pertama diperbolehkan untuk mengambil batu sebanyak bilangan positif apapun, namun tidak diperbolehkan mengambil semua batu.
Kemudian, setiap pemain diperbolehkan untuk mengambil batu paling banyak dua kali lipat dari jumlah batu yang diambil oleh pemain lain pada giliran sebelumnya.
Pemain yang mengambil batu terakhir menang.
Sebagai contoh, saat n=5
Jika pemain pertama mengambil lebih dari satu batu, maka pemain kedua akan dapat mengambil semua batu pada giliran selanjutnya.
Jika pemain pertama mengambil satu batu pada giliran pertama, akan tersisa empat batu, lawannya juga kemudian akan mengambil satu batu, Menyisakan tiga batu.
Pemain pertama tidak dapat mengambil ketiga batu yang tersisa, karena ia hanya bisa mengambil paling banyak 2x1=2 batu. Sehingga mari kita asumsikan ia juga mengambil satu buah batu, sehingga tersisa 2. Maka pemain kedua dapat mengambil semua batu yang masih tersisa dan menjadi pemenang.
Sehingga n=5 adalah jumlah batu yang menghasilkan kekalahan untuk pemain pertama.
Untuk beberapa jumlah batu yang menghasilkan kemenangan terdapat lebih dari satu gerakan yang mungkin dilakukan oleh pemain pertama.
Sebagai contoh, saat n=17 pemain pertama dapat mengambil satu atau empat batu.
Misal M(n) adalah banyaknya batu yang dapat diambil oleh pemain pertama pada jumlah batu yang menghasilkan kemenangan pada giliran pertama dan M(n)=0 untuk banyak batu lainnya.
∑M(n) untuk n≤100 is 728.
Carilah ∑M(n) untuk n≤1018. Berikan jawaban Anda yang telah di modulo 108.
Answer: 8a080de12c5163d903b6212dd8086570
Soal 367
Sortiran Bozo, bedakan dengan metode sortiran bogo yang kurang efisien, dilakukan dengan cara memeriksa apakah barisan input yang ada telah disortir, jika belum maka dilakukan penukaran dua elemen secara acak. Penukaran ini dilakukan terus menerus sampai barisan sudah berurutan.
Jika kita menggunakan semua permutasi dari 4 bilangan asli pertama sebagai input, rata-rata banyaknya proses penukaran yang terjadi, dari semua 4! permutasi yang mungkin dari input adalah 24.75.
Barisan yang telah berurutan dianggap memerlukan 0 kali penukaran.
Pada permasalahan ini, kita akan menggunakan variasi sortiran bozo berikut ini.
Jika barisan belum berurutan, kita akan mengambil tiga elemen secara acak, dan menukar posisi ketiga elemen tersebut juga secara acak.
Ke 3!=6 permutasi yang mungkin dari tiga elemen tersebut akan menghasilkan hasil yang sama.
Barisan yang sudah berurutan dianggap memerlukan 0 kali penukaran.
Jika kita menggunakan input berupa permutasi dari 4 bilangan asli pertama, dugaan rata-rata banyaknya penukaran yang dilakukan, terhadap semua 4! permutasi yang mungkin dari input menggunakan variasi ini adalah 27.5.
Jika barisan input yang digunakan adalah permutasi dari 11 bilangan asli pertama.
berapakah dugaan rata-rata banyaknya penukaran yang dilakukan untuk 11! permutasi yang mungkin, dengan algoritma ini?
Berikan jawaban Anda yang dibulatkan ke bilangan bulat terdekat.
Answer: 0589f090524e0eea1544b50eefd0ebd8
Soal 368
| Sebuah barisan harmonik 1 | + |
|
+ |
|
+ |
|
+ ... diketahui adalah merupakan barisan divergen. |
Tetapi jika kita menghilangkan dari barisan ini setiap suku yang pada penyebutnya terdapat angka 9, maka barisan ini kira-kira akan konvergen ke 22.9206766193.
Hasil modifikasi barisan harmonik ini disebut sebagai barisan Kempner.
Sekarang mari kita memperhatikan hasil modifikasi lain dari barisan harmonik, dengan menghilangkan setiap suku yang pada penyebutnya terdapat 3 buah atau lebih digit yang sama secara berurutan.
Dapat dibuktikan bahwa dari 1200 suku pertama barisan harmonik, hanya terdapat 20 suku yang akan dihilangkan.
Ke-20 buah suku yang akan dihilangkan adalah:
|
, |
|
, | <table class="frac"style="text-align:center;"> |
| 1 |
| 333 | , |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
, |
|
and |
|
. |
Barisan ini juga akan memiliki hasil konvergen.
Carilah menuju ke nilai berapakah barisan ini akan konvergen.
Berikan jawaban Anda dibulatkan hingga 10 angka di belakang koma.
Answer: bfb15c388f4721cbd5eb89f17be2eef2
Soal 369
Pada dek kartu standar berisi 52 kartu, sebuah set berisi 4 kartu adalah sebuah Badugi jika tidak terdapat dua kartu yang bernilai sama, dan juga tidak terdapat dua kartu yang memiliki jenis (Spade, Heart, Diamond, Club) yang sama.
Misal f(n) adalah banyaknya cara untuk memilih n buah kartu, dengan 4 buah kartu padanya yang merupakan sebuah Badugi. Sebagai contoh, terdapat 2598960 cara untuk memilih lima buah kartu dari dek kartu standar berisi 52 kartu, dimana terdapat 514800 susunan 4 buah kartu padanya yang merupakan sebuah Badugi, sehingga f(5) = 514800.
Carilah ∑f(n) untuk 4 ≤ n ≤ 13.
Answer: 0f8828f58dbac4f15f296c79b686ed0e
Soal 370
Mari kita nyatakan sebuah segitiga geometrik sebagai sebuah segitiga dengan panjang sisi bilangan bulat a ≤ b ≤ c, sehingga semua sisinya membentuk sebuah deret geometri, sehingga b2 = a · c .
Sebuah contoh dari segitiga seperti ini adalah segitiga dengan panjang sisi a = 144, b = 156 dan c = 169.
Terdapat 861805 buah segitiga geometrik dengan panjang keliling ≤ 106 .
Berapa banyak segitiga geometrik yang ada dengan panjang keliling ≤ 2.5·1013 ?
Answer: 85b5048e25677205555a5308991c2e04
Soal 371
Plat nomor kendaraan Oregon terdiri dari tiga huruf diikuti oleh tiga digit angka (setiap digit dapat dipilih dari [0..9]).
Saat mengemudikan kendaraan ke tempat kerja, Seth memainkan permainan ini:
Saat ia melihat plat nomor dari dua kendaraan yang hasil penjumlahanannya 1000, ia menang.
Sebagai contoh, jika ia melihat plat nomor MIC-012 dan HAN-988, maka ia menang, dan juga plat nomor RYU-500 dan SET-500. (selama ia melihat kedua plat tersebut dalam satu perjalanan yang sama).
Carilah nilai harapan (expected number), agar ia dapat melihat plat nomor yang menjadikannya menang.
Berikan jawaban Anda dibulatkan hingga 8 angka di belakang koma.
Catatan: Kita asumsikan setiap plat nomor yang terlihat memiliki peluang yang sama untuk memiliki bilangan 3 digit apapun padanya.
Answer: 537403a97924621c604ce5ab6288b97d
Soal 372
Misal R(M, N) adalah banyaknya titik koordinat bilangan bulat (x, y) yang memenuhi M<x≤N, M<y≤N dan  adalah bilangan ganjil.
adalah bilangan ganjil.
Dapat dibuktikan bahwa R(0, 100) = 3019 dan R(100, 10000) = 29750422.
Carilah R(2·106, 109).
Catatan:  memiliki arti fungsi pembulatan ke bawah.
memiliki arti fungsi pembulatan ke bawah.
</p>
Answer: 5fdeda0dca23d12ae3eb1763b2c6f5ea
Soal 373
Setiap segitiga memiliki sebuah lingkaran luar segitiga yang melalui ketiga titik sudut segitiga tersebut. Perhatikan bahwa semua segitiga yang memiliki panjang sisi berupa bilangan bulat, akan memiliki lingkaran luar segitiga dengan panjang jari-jari yang juga berupa bilangan bulat.
Misal S(n) adalah hasil penjumlahan panjang jari-jari lingkaran luar segitiga dari semua segitiga, yang panjang jari-jari lingkaran luar segitiganya tidak melebihi n.
S(100)=4950 dan S(1200)=1653605.
Carilah S(107).
Answer: 888d60a6b2b4b9146d7c9c14ffd82673
Soal 374
Partisi bilangan bulat dari suatu bilangan n adalah sebuah cara untuk menuliskan n sebagai hasil penjumlahan dari bilangan bulat positif.
Partisi yang hanya memiliki perbedaan urutan dari bilangan-bilangan penyusunnya dianggap sama. Sebuah partisi dari n yang partisi berbeda adalah sebuah partisi dari n dimana setiap penyusunnya hanya muncul paling banyak sekali.
Partisi dari 5 ke dalam partisi berbeda adalah:
5, 4+1 dan 3+2.
Misal f(n) adalah hasil perkalian terbesar dari penyusun-penyusun partisi berbeda dari n, dan misalkan m(n) adalah banyaknya penyusun dari partisi n yang memiliki hasil perkalian tersebut.
Sehingga f(5)=6 dan m(5)=2.
Untuk n=10 hasil partisi yang memiliki hasil perkalian terbesar adalah 10=2+3+5, yang akan memberikan hasil f(10)=30 dan m(10)=3.
Dan hasil kali keduanya, f(10)·m(10) = 30·3 = 90
Dapat dibuktikan bahwa
∑f(n)·m(n) untuk 1 ≤ n ≤ 100 = 1683550844462.
Carilah ∑f(n)·m(n) untuk 1 ≤ n ≤ 1014.
Berikan jawaban Anda yang telah di modulo 982451653, bilangan prima yang ke-50 juta.
Answer: 6fcb063062076b5aaaff3e3cd03e4b2f
Soal 375
Misal Sn adalah sebuah barisan bilangan bulat yang dihasilkan dengan fungsi pembentuk bilangan acak berikut:
| S0 | = | 290797 |
| Sn+1 | = | Sn2 mod 50515093 |
Misal A(i, j) adalah nilai minimum yang terdapat pada Si, Si+1, ... , Sj untuk i ≤ j.
Misal M(N) = ΣA(i, j) untuk 1 ≤ i ≤ j ≤ N.
Kita dapat membuktikan bahwa M(10) = 432256955 dan M(10 000) = 3264567774119.
Carilah M(2 000 000 000).
Answer: 68a12e3f2e4ccbae9c8555e547fbe096
Soal 376
Perhatikan dadu-dadu berikut ini yang memiliki angka tidak standar:
Dadu A: 1 4 4 4 4 4
Dadu B: 2 2 2 5 5 5
Dadu C: 3 3 3 3 3 6
Sebuah permainan dimainkan oleh dua orang dengan cara mengambil sebuah dadu dan melemparkannya. Pemain yang megeluarkan angka dadu terbesar menjadi pemenang.
Jika pemain pertama memilih dadu A dan pemain kedua memilih dadu B, kita dapatkan
P(pemain kedua menang) = 7/12 > 1/2
Jika pemain pertama memilih dadu B dan pemain kedua memilih dadu C, kita dapatkan
P(pemain kedua menang) = 7/12 > 1/2
Jika pemain pertama memilih dadu C dan pemain kedua memilih dadu A, kita dapatkan
P(pemain kedua menang) = 25/36 > 1/2
Sehingga apapun dadu yang dipilih oleh pemain pertama, pemain kedua selalu dapat memilih dadu lain yang memiliki peluang lebih dari 50% untuk menang.
Seperangkat dadu yang memiliki sifat ini disebut sebagai set dadu nontransitif.
Kita ingin menyelidiki berapa banyak set dadu nontransitif yang ada. Kita akan asumsikan dengan keadaan berikut:
- Terdapat tiga buah dadu dengan enam buah sisi, yang setiap sisinya memiliki angka antara 1 dan N, 1 dan N termasuk.
- Dadu-dadu yang memiliki angka-angka yang sama dianggap sama, walaupun mungkin terdapat perbedaan posisi dari angka-angka yang ada pada setiap dadu.
- Munculnya angka yang sama antara beberapa dadu setelah dilemparkan dapat saja terjadi; jika kedua pemain mendapatkan angka yang sama, maka tidak ada pemain yang menang.
- Set dadu {A,B,C}, {B,C,A} dan {C,A,B} adalah merupakan set yang sama.
Untuk N = 7 terdapat 9780 set seperti di atas.
Berapa banyak set yang ada untuk N = 30 ?
Answer: c64df302990eb3738f8ec62ea6b66c0b
Soal 377
Terdapat 16 bilangan bulat positif yang tidak terdapat angka nol pada digit-digitnya, dan memiliki hasil penjumlahan digit-digit sama dengan 5, yaitu:
5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 dan 11111.
Hasil penjumlahan mereka semua adalah 17891.
Misal f(n) adalah hasil penjumlahan semua bilangan bulat positif yang tidak memiliki angka nol pada digit-digitnya, dan memiliki hasil penjumlahan digit-digit sama dengan n.
Carilah $\displaystyle \sum_{i=1}^{17} f(13^i)$.
Berikan 9 digit terakhir dari jawaban Anda.
Answer: a915ccbae49de15208c88affba84d206
Soal 378
| Misal T(n) adalah bilangan segitiga ke-n, sehingga T(n) = |
|
. |
Misal dT(n) adalah banyaknya faktor dari T(n).
Sebagai contoh:
T(7) = 28 dan dT(7) = 6.
Misal Tr(n) adalah bilangan tripel (i, j, k) sehingga 1 ≤ i < j < k ≤ n dan dT(i) > dT(j) > dT(k).
Tr(20) = 14, Tr(100) = 5772 dan Tr(1000) = 11174776.
Carilah Tr(60 000 000).
Berikan 18 digit terakhir dari jawaban Anda.
Answer: 336745dc9d90928596237c4b471a8927
Soal 379
Misal f(n) adalah banyaknya pasangan (x,y) dengan x dan y berupa bilangan bulat positif, x ≤ y dan kelipatan persekutuan terkecil dari x dan y sama dengan n.
Dan misal g adalah fungsi penjumlahan dari f, sehingga: g(n) = ∑ f(i) untuk 1 ≤ i ≤ n.
Anda diberikan informasi bahwa g(106) = 37429395.
Carilah g(1012).
Answer: de20f710cb6665c48795072197ad53e0
Soal 380
Sebuah labirin berukuran m×n adalah sebuah persegi panjang berukuran m×n berisi kotak-kotak, dengan dinding-dinding yang diletakkan antara kotak-kotak, sehingga terdapat persis satu jalur dari persegi di pojok kiri atas ke persegi lainnya.
Berikut ini adalah contoh dari labirin berukuran 9×12 dan labirin berukuran 15×20:

Misal C(m,n) adalah banyaknya labirin berukuran m×n berbeda. Labirin yang dibuat dari hasil rotasi dan refleksi labirin lain dianggap berbeda.
Dapat dibuktikan bahwa C(1,1) = 1, C(2,2) = 4, C(3,4) = 2415, dan C(9,12) = 2.5720e46 (dalam notasi ilmiah dibulatkan hingga 5 angka penting).
Carilah C(100,500) dan tuliskan jawaban Anda dalam notasi ilmiah dibulatkan hingga 5 angka penting.
Saat memberikan jawaban Anda, gunakan huruf kecil e untuk memisahkan mantissa dan eksponen. Sebagai contoh, jika jawaban Anda adalah 1234567891011, maka format jawabannya adalah 1.2346e12.
Answer: c86d2f4c17c8134fbebed5d37a0f90d7
Soal 381
Untuk sebuah bilangan prima p, S(p) = (∑(p-k)!) mod(p) untuk 1 ≤ k ≤ 5.
Sebagai contoh, jika p=7,
(7-1)! + (7-2)! + (7-3)! + (7-4)! + (7-5)! = 6! + 5! + 4! + 3! + 2! = 720+120+24+6+2 = 872.
Dan 872 mod(7) = 4, sehingga S(7) = 4.
Dapat dibuktikan bahwa ∑S(p) = 480 untuk 5 ≤ p < 100.
Carilah ∑S(p) untuk 5 ≤ p < 108.
Answer: 80c84973a9643e46d49d79d7284e7ff3
Soal 382
Poligon adalah sebuah bidang tipis yang terdiri dari segmen garis lurus yang dihubungkan untuk membentuk rantai atau jalur tertutup. Sebuah poligon terdiri dari setidaknya tiga buah sisi dan semua sisinya tidak saling memotong satu sama lain.
Sebuah himpunan S yang berisi bilangan positif dapat disebut dapat membentuk sebuah poligon P jika:
- tidak terdapat dua sisi dari P yang memiliki panjang yang sama,
- panjang dari setiap sisi P adalah merupakan anggota S, dan
- S tidak memiliki anggota lain yang bukan merupakan panjang sisi pada P.
Sebagai contoh:
Himpunan {3, 4, 5} membentuk sebuah poligon dengan panjang sisi 3, 4, dan 5 (sebuah segitiga).
Himpunan {6, 9, 11, 24} membentuk sebuah poligon dengan panjang sisi 6, 9, 11, dan 24 (sebuah bangun bersisi empat).
Himpunan {1, 2, 3} dan {2, 3, 4, 9} tidak dapat membentuk poligon sama sekali.
Perhatikan barisan bilangan s, yang dinyatakan sebagai berikut:
- s1 = 1, s2 = 2, s3 = 3
- sn = sn-1 + sn-3 for n > 3.
Misal Un adalah himpunan {s1, s2, ..., sn}. Sebagai contoh, U10 = {1, 2, 3, 4, 6, 9, 13, 19, 28, 41}.
Misal f(n) adalah banyaknya himpunan bagian dari Un yang akan membentuk setidaknya satu buah poligon.
Sebagai contoh, f(5) = 7, f(10) = 501 dan f(25) = 18635853.
Carilah 9 digit terakhir dari f(1018).
Answer: 56a121bcf3bb674d0d3ce561b6b24ea5
Soal 383
Misal f5(n) adalah bilangan bulat terbesar x dimana 5x habis membagi n.
Sebagai contoh, f5(625000) = 7.
Misal T5(n) adalah banyaknya bilangan bulat i yang memenuhi f5((2·i-1)!) < 2·f5(i!) dan 1 ≤ i ≤ n.
Dapat dibuktikan bahwa T5(103) = 68 dan T5(109) = 2408210.
Carilah T5(1018).
Answer: c1bc7c945344e1967bfaced9ade895a0
Soal 384
Dinyatakan barisan a(n) sebagai banyaknya pasangan dua buah angka satu yang bersebelahan, pada penjabaran biner dari n (setiap angka satu dapat digunakan berkali-kali).
Sebagai contoh: a(5) = a(1012) = 0, a(6) = a(1102) = 1, a(7) = a(1112) = 2
Dinyatakan barisan b(n) = (-1)a(n).
Barisan ini disebut sebagai barisan Rudin-Shapiro.
Perhatikan juga barisan dari hasil penjumlahan b(n):

Beberapa pasangan pertama dari barisan ini adalah:
n   0   1   2   3   4   5   6   7
a(n)   0   0   0   1   0   0   1   2
b(n)   1   1   1   -1   1   1   -1   1
s(n)   1   2   3   2   3   4   3   4
Barisan s(n) memiliki sifat luar biasa, yaitu semua elemennya adalah bilangan positif, dan semua bilangan bulat positif k muncul persis k kali.
Dinyatakan g(t,c), dengan 1 ≤ c ≤ t, sebagai indeks pada s(n) dimana angka t muncul untuk ke c-kalinya pada s(n).
Sebagai contoh: g(3,3) = 6, g(4,2) = 7 dan g(54321,12345) = 1220847710.
Misal F(n) adalah barisan fibonacci yang dinyatakan oleh:
F(0)=F(1)=1 dan
F(n)=F(n-1)+F(n-2) untuk n>1.
Dinyatakan GF(t)=g(F(t),F(t-1)).
Carilah ΣGF(t) untuk 2≤t≤45.
Answer: ea0bb1fff1a51b48971762b93aeed103
Soal 385
Untuk setiap segitiga T pada suatu bidang datar, dapat ditunjukkan bahwa terdapat elips unik dengan luas terbesar yang semua bagian elipsnya berada di dalam T.

Untuk nilai n yang diketahui, segitiga T akan memiliki ketentuan:
- titik sudut dari T mempunyai koordinat berupa bilangan bulat dengan nilai absolut ≤ n, dan
- titik foci1 dari elips yang memiliki luas terbesar di dalam T adalah (√13,0) dan (-√13,0).
Misal A(n) adalah hasil penjumlahan dari luas semua segitiga seperti ini.
Sebagai contoh, jika n = 8, terdapat dua buah segitiga seperti ini. Titik-titik sudutnya adalah (-4,-3),(-4,3),(8,0) dan (4,3),(4,-3),(-8,0), dan luas dari setiap segitiga adalah 36. Sehingga A(8) = 36 + 36 = 72.
Dapat dibuktikan bahwa A(10) = 252, A(100) = 34632 dan A(1000) = 3529008.
Carilah A(1 000 000 000).
1Titik foci (atau dapat disebut titik fokus) dari sebuah elips adalah dua titik A dan B, sehingga setiap titik P pada keliling elips akan memiliki nilai AP + PB yang konstan.
Answer: a21c033d9e119c293e51966ea78c9950
Soal 386
Misal n adalah sebuah bilangan bulat dan S(n) adalah himpunan faktor dari n.
Sebuah himpunan bagian A dari S(n) disebut sebagi sebuah anti rantai dari S(n) jika A berisi hanya satu elemen, atau jika tidak ada elemen dari A yang dapat membagi habis elemen lainnya di A.
Sebagai contoh: S(30) = {1, 2, 3, 5, 6, 10, 15, 30}
{2, 5, 6} bukanlah anti rantai dari S(30).
{2, 3, 5} adalah anti rantai dari S(30).
Misal N(n) adalah banyaknya anggota maksimum dari anti rantai S(n).
Carilah ΣN(n) untuk 1 ≤ n ≤ 108
Answer: d1d893f7c50910aa10daec5e9352e86d
Soal 387
Sebuah bilangan Harshad atau bilangan Niven adalah sebuah bilangan yang habis dibagi oleh hasil penjumlahan digit-digitnya.
201 adalah sebuah bilangan Harshad, karena bilangan ini habis dibagi 3 (yang merupakan hasil penjumlahan digit-digitnya.)
Saat kita memotong digit terakhir dari 201, kita dapatkan 20, yang juga merupakan bilangan Harshad.
Saat kita memotong digit terakhir dari 20, kita dapatkan 2, yang juga merupakan bilangan Harshad.
Mari kita sebut bilangan Harshad, yang saat digit terakhirnya terus menerus dipotong, masih selalu menghasilkan sebuah bilangan Harshad sebagai bilangan Harshad yang dapat dipotong sebelah kanan.
Juga:
201/3=67 dimana bilangan ini merupakan bilangan prima.
Mari kita sebut bilangan Harshad, yang saat dibagi oleh hasil penjumlahan digit-digitnya, akan menghasilkan bilangan prima sebagai bilangan Harshad kuat.
Sekarang perhatikan bilangan 2011 yang merupakan sebuah bilangan prima.
Saat kita memotong digit terakhir darinya kita akan mendapatkan 201, sebuah bilangan Harshad kuat dan juga bilangan Harshad yang dapat dipotong di sebelah kanan.
Mari kita sebut bilangan prima seperti ini sebagai bilangan prima Harshad kuat dan dapat dipotong sebelah kanan.
Diketahui hasil penjumlahan dari semua bilangan prima Harshad kuat dan dapat dipotong sebelah kanan kurang dari 10000 adalah 90619.
Carilah hasil penjumlahan dari semua bilangan prima Harshad kuat dan dapat dipotong sebelah kanan kurang dari 1014.
Answer: a20cbd8639767decfa2c2c9955eb6be3
Soal 388
Perhatikan semua titik dengan koordinat bilangan bulat(a,b,c) dengan 0 ≤ a,b,c ≤ N.
Dari titik origin O(0,0,0), semua garis digambarkan menuju titik lain.
Misal D(N) adalah banyaknya garis berbeda yang digambarkan.
Diketahui bahwa D(1 000 000) = 831909254469114121.
Carilah D(1010). Berikan sembilan digit pertama dari jawaban Anda diikuti dengan 9 digit terakhir dari jawaban Anda.
Answer: 2bab886c7d98d802d9249c9e12d72c25
Soal 389
Sebuah dadu bersisi 4 dilemparkan dan mengeluarkan angka T, kemudian angka tersebut dicatat.
T buah dadu bersisi 6 dilemparkan dan nilai dari semua hasil lemparan ini dijumlahkan. Hasil penjumlahannya C kemudian dicatat.
C buah dadu bersisi 8 dilemparkan dan nilai dari semua hasil lemparan ini dijumlahkan. Hasil penjumlahannya O kemudian dicatat.
O buah dadu bersisi 12 dilemparkan dan nilai dari semua hasil lemparan ini dijumlahkan. Hasil penjumlahannya D kemudian dicatat.
D buah dadu bersisi 20 dilemparkan dan nilai dari semua hasil lemparan ini dijumlahkan. Hasil penjumlahannya I kemudian dicatat.
Carilah variance atau ragam dari I, dan berikan jawaban Anda yang telah dibulatkan hingga 4 angka di belakang koma.
Answer: 79a080d38b837547b975c97b44764dfb
Soal 390
Perhatikan segitiga dengan panjang sisi √5, √65 dan √68. Dapat ditunjukkan bahwa segitiga ini memiliki luas 9.
S(n) adalah hasil penjumlahan dari luas semua segitiga dengan panjang sisi √(1+b2), √(1+c2) dan √(b2+c2) (untuk bilangan bulat positif b dan c ), yang memiliki luas berupa bilangan bulat dan tidak melebihi n.
Salah satu contoh segitiga yang memenuhi sifat di atas memiliki b=2 dan c=8.
S(106)=18018206.
Carilah S(1010).
Answer: ed7f2fbc05a2fd2033d80de671f35ea3
Soal 391
Misal sk adalah banyaknya angka 1 saat menulis bilangan-bilangan dari 0 sampai k dalam bentuk biner.
Sebagai contoh, jika kita menulis 0 sampai 5 dalam biner, maka kita dapatkan 0, 1, 10, 11, 100, 101. Terdapat tujuh buah angka 1, sehingga s5 = 7.
Barisan S = {sk : k ≥ 0} berisi {0, 1, 2, 4, 5, 7, 9, 12, ...}.
Sebuah permainan dimainkan oleh dua orang. Sebelum permainan dimulai, sebuah bilangan n dipilih. Sebuah penghitung (counter) c dimulai dari 0. Pada setiap giliran, pemain memilih sebuah angka antara 1 sampai n (1 dan n juga termasuk ke dalam pilihan) dan menambahkan c dengan angka tersebut. Hasil dari nilai c yang baru haruslah merupakan anggota S. Jika tidak ada lagi angka yang bisa dipilih yang memenuhi aturan ini, maka pemain tersebut kalah.
Sebagai contoh:
Misal n = 5. c dimulai dari 0.
Pemain 1 memilih angka 4, sehingga c menjadi 0 + 4 = 4.
Pemain 2 memilih angka 5, sehingga c menjadi 4 + 5 = 9.
Pemain 1 memilih angka 3, sehingga c menjadi 9 + 3 = 12.
dan seterusnya.
Perlu diingat bahwa nilai c harus selalu terdapat di S, dan setiap pemain dapat menambahkan nilai c paling banyak sebesar n.
Misal M(n) adalah bilangan tertinggi yang bisa dipilih oleh pemain pertama pada giliran pertama untuk memastikan kemenangan, dan M(n) = 0 jika tidak ada bilangan yang memungkinkan pemain pertama untuk menang. Sebagai contoh, M(2) = 2, M(7) = 1 dan M(20) = 4.
Diberikan Σ(M(n))3 = 8150 untuk 1 ≤ n ≤ 20.
Carilah Σ(M(n))3 untuk 1 ≤ n ≤ 1000.
Answer: b2947548d4f5c4878c5f788f9849e750
Soal 392
Sebuah kisi rectilinear adalah sebuah kisi ortogonal, dimana jarak antara dua buah garis kisinya tidak harus sama satu dengan yang lain.
Salah satu contoh kisi seperti ini adalah kertas grafik logaritmik (logarithmic graph paper).
Perhatikan kisi rectilinear pada sistem koordinat Kartesius, dengan sifat-sifat berikut:
- Garis-garis kisinya adalah sejajar dengan sumbu pada sistem koordinat Kartesius.
- Terdapat N+2 garis kisi vertikal dan N+2 garis kisi horizontal. Sehingga akan terdapat (N+1) x (N+1) buah sel persegi panjang.
- Persamaan dari dua garis kisi vertikal terluar adalah x = -1 dan x = 1.
- Persamaan dari garis kisi horizontal terluar adalah y = -1 dan y = 1.
- Sel persegi panjang akan diberi warna merah apabila ia bertumpukan dengan sebuah lingkaran satuan, selain itu sel persegi panjang akan diberi warna hitam.
Sebagai contoh, berikut ini adalah gambar solusi untuk N = 10:

Luas daerah yang dimiliki oleh sel bewarna merah untuk N = 10 dibulatkan hingga 10 angka di belakang koma adalah 3.3469640797.
Carilah posisi garis-garis kisi untuk N = 400.
Sebagai jawaban Anda, berikan luas daerah yang dimiliki oleh sel bewarna merah dibulatkan hingga 10 angka di belakang koma.
Answer: 3268b0bc489187db3d234c097040d909
Soal 393
Pada sebuah kisi berukuran n×n terdapat n2 ekor semut, satu semut pada setiap persegi di kisi tersebut.
Semua semut memutuskan untuk berpindah secara bersamaan ke persegi di sebelahnya (biasanya terdapat 4 kemungkinan arah, kecuali untuk semut yang berada di persegi-persegi pojok).
Kita nyatakan f(n) sebagai banyaknya cara hal ini dapat terjadi tanpa ada satu semutpun yang masih berada di kotak yang sama, dan tanpa ada dua semut yang melintasi sisi persegi yang sama.
Diketahui f(4) = 88.
Carilah f(10).
Answer: 58e4990838fb3d1725872da30f9db748
Soal 394
Jeff memakan sebuah kue pai dengan cara yang tidak biasa.
Kue pai tersebut berbetuk lingkaran. Ia memulai dengan membuat sebuah potongan pertama pada kue pai sepanjang jari-jari lingkaran.
Saat terdapat F bagian dari kue pai yang masih tersisa, ia melakukan prosedur berikut ini:
- Ia membuat dua buah potongan dari pusat kue pai ke titik manapun di pinggir kue pai yang masih tersisa, semua titik pada keliling kue pai memiliki peluang yang sama untuk dipilih. Dan potongan ini akan membagi kue pai yang masih tersisa menjadi tiga bagian.
- Berlawanan arah jarum jam dari potongan pertama, ia mengambil dua potongan kue pai pertama dan memakannya.
Saat terdapat sisa kue pai kurang dari F bagian, ia tidak melakukan prosedur di atas lagi. Melainkan, ia akan memakan semua kue pai yang masih tersisa.

</p>
Untuk x ≥ 1, misal E(x) adalah nilai harapan (expected number) dari banyaknya prosedur di atas diulang oleh Jeff dengan F = 1/x.
Dapat dibuktikan bahwa E(1) = 1, E(2) ≈ 1.2676536759, dan E(7.5) ≈ 2.1215732071.
Carilah E(40) dibulatkan hingga 10 angka di belakang koma.
Answer: f8ad575e1a03365a60b6429c3b7a64df
Soal 395
Pohon Pythagoras adalah sebuah fractal yang dibuat dengan prosedur sebagai berikut:
Dimulai dari sebuah persegi dengan panjang sisi 1. Kemudian, kemudian salah satu sisi akan disebut sebagai alas (pada animasi, sisi sebelah bawah persegi adalah alasnya):
- Tempelkan sebuah segitiga siku-siku ke sisi yang ada di seberang alas, dengan hipotenusa segitiga berhimpit dengan sisi tersebut, dan dengan perbandingan sisi segitiga 3-4-5. Perlu diingat bahwa sisi yang lebih pendek dari segitiga harus ada di bagian 'kanan' dari alas persegi (perhatikan animasi).
- Tempelkan sebuah persegi ke setiap kaki-kaki dari segitiga siku-siku, dengan satu dari sisi persegi tersebut berhimpit dengan kaki segitiga tersebut.
- Ulangi prosedur ini untuk kedua buah persegi, yang dianggap sebagai alas kedua persegi yang baru adalah sisi yang menempel dengan segitiga.

Dapat ditunjukkan bahwa terdapat setidaknya satu buah persegi, yang sisinya sejajar dengan persegi paling besar pada pohon Pythagoras, dimana persegi tersebut akan menutup pohon Pythagoras dengan sempurna.
Carilah kemungkinan luas terkecil untuk persegi penutup tersebut, dan berikan jawaban Anda dibulatkan hingga 10 angka di belakang koma.
Answer: 505048b0c619161d05b9b3e492f3edc3
Soal 396
Untuk setiap bilangan bulat positif n, barisan Goodstein lemah ke-n {g1, g2, g3, ...} dinyatakan dengan:
- g1 = n
- untuk k > 1, gk didapatkan dengan cara menuliskan gk-1 dalam basis k, kemudian mengubahnya menjadi bilangan basis k + 1, dan menguranginya dengan 1.
Sebagai contoh, barisan Goodstein lemah ke-6 adalah {6, 11, 17, 25, ...}:
- g1 = 6.
- g2 = 11 karena 6 = 1102, 1103 = 12, dan 12 - 1 = 11.
- g3 = 17 karena 11 = 1023, 1024 = 18, dan 18 - 1 = 17.
- g4 = 25 karena 17 = 1014, 1015 = 26, dan 26 - 1 = 25.
Dapat ditunjukkan bahwa semua barisan Goodstein lemah pasti akan berhenti.
Misal G(n) adalah banyaknya elemen tidak nol pada barisan Goodstein lemah ke-n.
Dapat dibuktikan bahwa G(2) = 3, G(4) = 21 dan G(6) = 381.
Dapat juga dibuktikan bahwa ΣG(n) = 2517 untuk 1 ≤ n < 8.
Carilah 9 digit terakhir dari ΣG(n) untuk 1 ≤ n < 16.
Answer: 4665c73fdca473ccc0643fc982f24e06
Soal 397
Pada parabola y = x2/k, dipilih tiga buah titik A(a, a2/k), B(b, b2/k) dan C(c, c2/k).
Misal F(K, X) adalah banyaknya pasangan bilangan bulat (k, a, b, c), sehingga setidaknya salah satu sudut dari segitiga ABC adalah 45-derajat, dengan 1 ≤ k ≤ K dan -X ≤ a < b < c ≤ X.
Sebagai contoh, F(1, 10) = 41 and F(10, 100) = 12492.
Carilah F(106, 109).
Answer: 07f769df9543bc05e6318878c34d074d
Soal 398
Pada sebuah tali dengan panjang n, n-1 buah titik diletakkan dengan jarak 1 antar titik dimulai dari ujung tali. Antara titik-titik tersebut, kita akan memilih m-1 buah titik secara acak, dan memotong tali tersebut pada titik=titik yang ada untuk membuat m buah potongan tali.
Misal E(n, m) adalah panjang perkiraan (expected length) dari potongan tali yang kedua terpendek.</BR> Sebagai contoh, E(3, 2) = 2 dan E(8, 3) = 16/7.</BR> Perlu diingat bahwa jika terdapat lebih dari satu buah potongan tali yang memiliki panjang yang sama dengan tali terpendek, maka panjang tali yang terpendek kedua adalah panjang tali yang terpendek.
Carilah E(107, 100).</BR> berikah jawaban Anda dibulatkan hingga 5 angka di belakang koma.
Answer: fa0a25d62fa225e05fd8736713a9bfc0
Soal 399
15 bilangan fibonacci pertama adalah:
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610.
Dapat terlihat bahwa 8 dan 144 bukanlah bilangan squarefree: 8 habis dibagi oleh 4 dan 144 habis dibagi oleh 4 dan oleh 9.
Sehingga 13 bilangan fibonacci squarefree pertama adalah:
1,1,2,3,5,13,21,34,55,89,233,377 and 610.
Bilangan fibonacci squarefree ke-200 adalah:
971183874599339129547649988289594072811608739584170445.
Enam belas digit terakhir dari bilangan ini adalah: 1608739584170445 dan dalam notasi ilmiah, bilangan ini dapat ditulis sebagai 9.7e53.
Carilah bilangan fibonacci squarefree ke-100 000 000.
Berikan jawaban Anda berupa enam belas digit terakhirnya, diikuti oleh sebuah tanda koma, diikuti oleh bilangan tersebut yang ditulis dalam notasi ilmiah (dibulatkan hingga satu angka di belakang koma).
Untuk bilangan fibonacci squarefree ke-200, jawabannya akan menjadi: 1608739584170445,9.7e53
<Font size=-1>
Catatan:
Untuk permasalahan ini, asumsikan untuk setiap bilangan prima p, bilangan fibonacci pertama yang habis dibagi oleh p tidak habis dibagi oleh p2 (ini merupakan bagian dari dugaan Wall). Dugaan ini telah dibuktikan untuk bilangan prima ≤ 3·1015, namun belum dapat dibuktikan secara umum.
Jika ternyata dugaan tersebut adalah salah, maka jawaban yang diterima oleh soal ini tidak dijamin sebagai bilangan fibonacci squarefree ke-100 000 000, tetapi jawaban soal ini hanya menyatakan batas bawah dari bilangan tersebut.
</FONT>
Answer: a0819cfe3be6a04645b8d4fe2345e184
Soal 400
Sebuah pohon Fibonacci adalah sebuah pohon biner yang secara rekursif dinyatakan dengan:
- T(0) adalah pohon kosong.
- T(1) adalah pohon biner (binary tree) yang hanya memiliki satu simpul (node).
- T(k) terdiri dari sebuah simpul akar (root node) yang mempunyai T(k-1) dan T(k-2) sebagai anaknya.
Pada pohon seperti ini, dua orang pemain memainkan sebuah permainan mengambil. Pada setiap giliran, seorang pemain memilih sebuah simpul dan mengambil simpul tersebut juga mengambil pohon yang berakar kepada simpul tersebut.
Pemain yang terpaksa harus mengambil simpul akar dari semua pohon adalah yang kalah.
Ini adalah gerakan kemenangan untuk pemain pertama pada giliran pertama untuk T(k) dari k=1 sampai k=6.

Misal f(k) adalah banyaknya gerakan kemenangan dari pemain pertama (yaitu gerakan yang menyebabkan pemain kedua tidak memungkinkan untuk menang) pada giliran pertama dari permainan, saat permainan dimainkan dengan T(k).
Sebagai contoh, f(5) = 1 dan f(10) = 17.
Carilah f(10000). Berikan 18 digit terakhir dari jawaban Anda.
Answer: 60aa790c07af1446c1e2deba72543a1f
Soal 401
Faktor dari 6 adalah 1,2,3 dan 6.
Hasil penjumlahan dari kuadrat bilangan-bilangan tersebut adalah 1+4+9+36=50.
Misal sigma2(n) menyatakan hasil penjumlahan kuadrat faktor-faktor dari n. Sehingga sigma2(6)=50.
Misal SIGMA2 menyatakan fungsi penjumlahan dari sigma2, sehingga SIGMA2(n)=∑sigma2(i) untuk i=1 sampai n.
6 nilai pertama untuk SIGMA2 adalah: 1,6,16,37,63 dan 113.
</P>
Carilah SIGMA2(1015) modulo 109.
Answer: 982a249d8b45ef10c98c32dabac00751
Soal 402
Dapat ditunjukkan bahwa polinom n4 + 4n3 + 2n2 + 5n adalah kelipatan 6 untuk setiap bilangan bulat n. Dapat juga ditunjukkan bahwa 6 adalah bilangan bulat terbesar yang memenuhi sifat ini.
Dinyatakan M(a, b, c) sebagai nilai m maksimum sehingga n4 + an3 + bn2 + cn adalah merupakan kelipatan dari m untuk setiap bilangan bulat n. Sebagai contoh, M(4, 2, 5) = 6.
Juga, dinyatakan S(N) sebagai hasil penjumlahan dari M(a, b, c) untuk semua 0 < a, b, c ≤ N.
Dapat kita buktikan bahwa S(10) = 1972 dan S(10000) = 2024258331114.
Misal Fk adalah barisan Fibonacci:
F0 = 0, F1 = 1 dan
Fk = Fk-1 + Fk-2 untuk k ≥ 2.
Carilah 9 digit terakhir dari Σ S(Fk) untuk 2 ≤ k ≤ 1234567890123.
Answer: fa7ae8e9243f01b0eac10ec5aaff1f42
Soal 403
Untuk bilangan bulat a dan b, kita nyatakan D(a, b) sebagai domain yang dibatasi oleh parabola y = x2 dan garis y = a·x + b:
D(a, b) = { (x, y) | x2 ≤ y ≤ a·x + b }.
L(a, b) dinyatakan sebagai banyaknya koordinat bilangan bulat yang terdapat di D(a, b).
Sebagi contoh, L(1, 2) = 8 dan L(2, -1) = 1.
Kita juga nyatakan S(N) sebagai hasil penjumlahan dari L(a, b) untuk semua pasangan (a, b) sehingga luas wilayah dari D(a, b) adalah merupakan bilangan rasional dan |a|,|b| ≤ N.
Dapat dibuktikan bahwa S(5) = 344 dan S(100) = 26709528.
Carilah S(1012). Berikan jawaban Anda yang telah di mod 108.
Answer: 31c018e3781a3e170366f01e30f09602
Soal 404
Ea adalah sebuah elips dengan persamaan x2 + 4y2 = 4a2.
Ea' adalah bayangan hasil rotasi dari Ea sejauh θ derajat berlawanan arah jarum jam dengan pusat rotasi origin O(0, 0) untuk 0° < θ < 90°.

b adalah jarak antara titik origin dengan dua titik potong yang terdekat ke origin, dan c adalah jarak serupa dengan dua titik potong lainnya.
Kita akan menyebut kumpulan bilangan (a, b, c) sebagai sebuah canonical ellipsoidal triplet jika a, b dan c adalah merupakan bilangan bulat positif.
Sebagai contoh, (209, 247, 286) adalah sebuah canonical ellipsoidal triplet.
Misal C(N) adalah banyaknya canonical ellipsoidal triplets (a, b, c) berbeda, dimana a ≤ N.
Dapat dibuktikan bahwa C(103) = 7, C(104) = 106 dan C(106) = 11845.
Carilah C(1017).
Answer: 2d1bc4b93bbc19d9e70c5b04338dea2e
Soal 405
Kita akan memasang ubin pada sebuah daerah berbentuk persegi panjang yang panjangnya dua kali lipat lebarnya.
Misal T(0) adalah sebuah persegi panjang.
Untuk n > 0, misal T(n) didaptkan dari T(n-1) dengan menggantikan semua persegi panjang dengan aturan berikut:

Animasi berikut ini mendemonstrasikan proses pemasangan ubin persegi panjang T(n) untuk n dari 0 sampai 5:

Misal f(n) adalah banyaknya titik dimana empat buah ubin bertemu pada T(n).
Sebagai contoh, f(1) = 0, f(4) = 82 dan f(109) mod 177 = 126897180.
Carilah f(10k) untuk k = 1018, berikan jawaban Anda yang telah di modulo 177.
Answer: 93b712426b768586f88d0bfe597842e6
Soal 406
Kita akan mencoba untuk mencari bilangan tersembunyi yang dipilih dari himpunan bilangan bulat {1, 2, ..., n} dengan memberikan pertanyaan.
Setiap bilangan (pertanyaan) yang kita tanyakan, akan memiliki satu dari tiga kemungkinan jawaban:
- "Tebakan Anda lebih rendah dari bilangan tersembunyi" (dan Anda harus mengeluarkan biaya sebesar a), atau
- "Tebakan Anda lebih tinggi dari bilangan tersembunyi" (dan Anda harus mengeluarkan biaya sebesar b), atau
- "Ya, itu jawabannya!" (dan permainan berakhir).
Diberikan nilai dari n, a, dan b, sebagai sebuah strategi optimal sehingga dapat meminimalisir total biaya untuk kasus terburuk.
Sebagai contoh, jika n = 5, a = 2, dan b = 3, maka kita dapat memulai dengan menanyakan "2" sebagai pertanyaan pertama kita.
Jika kita diberi tahu bahwa 2 lebih tinggi dari bilangan tersembunyi (dengan biaya sebesar b=3), maka dapat dipastikan oleh kita bahwa "1" adalah bilangan tersembunyi (untuk total biaya sebesar 3).
Jika kita diberi tahu bahwa 2 lebih rendah dari bilangan tersembunyi (dengan biaya sebesar a=2), maka pertanyaan kita selanjutnya akan menjadi "4".
Jika kita diberi tahu bahwa 4 lebih tinggi dari bilangan tersembunyi (dengan biaya sebesar b=3), maka dapat dipastikan oleh kita bahwa "3" adalah bilangan tersembunyi (untuk total biaya sebesar 2+3=5).
Jika kita diberi tahu bahwa 4 lebih rendah dari bilangan tersembunyi (dengan biaya sebesar a=2), maka dapat dipastikan oleh kita bahwa "5" adalah bilangan tersembunyi (untuk total biaya sebesar 2+2=4).
Sehingga, pada kasus terburuk, biayayang dikeluarkan oleh strategi ini adalah 5. Dan dapat dibuktikan bahwa ini merupakan kasus terburuk dengan biaya terkecil yang bisa didapatkan.
Bahkan, pada kenyataannya, kita baru saja menjelaskan sebuah strategi optimal untuk nilai n, a, dan b.
Misal C(n, a, b) adalah biaya yang didapatkan pada kasus terburuk, oleh sebuah strategi optimal jika diberikan nilai n, a, and b.
Berikut ini adalah beberapa contohnya:
C(5, 2, 3) = 5
C(500, √2, √3) = 13.22073197...
C(20000, 5, 7) = 82
C(2000000, √5, √7) = 49.63755955...
Misal Fk adalah bilangan Fibonacci: Fk = Fk-1 + Fk-2 dengan F1 = F2 = 1.
Carilah ∑1≤k≤30 C(1012, √k, √Fk), dan berikan jawaban Anda dibulatkan hingga 8 angka di belakang koma.
Answer: 0766b1ee975f5674d30fd6c3c934c6e0
Soal 407
Jika kita menghitung a2 mod 6 untuk 0 ≤ a ≤ 5 kita dapatkan: 0,1,4,3,4,1.
Bilangan a terbesar sehingga a2 ≡ a mod 6 adalah 4.
Mari kita sebut M(n) sebagai nilai terbesar dari a < n sehingga a2 ≡ a (mod n).
Sehingga M(6) = 4.
Carilah ∑M(n) untuk 1 ≤ n ≤ 107.
Answer: f4da34a4b357123cb142739a52e010f2
Soal 408
Mari kita sebut titik koordinat bilangan bulat (x, y) sebagai tidak bisa diterima jika x, y dan x + y semuanya adalah bilangan bulat kuadrat.
Sebagai contoh, (9, 16) adalah tidak bisa diterima, dimana (0, 4), (3, 1) dan (9, 4) adalah bukan.
Perhatikan jalur yang dibentuk dari titik (x1, y1) ke titik (x2, y2) hanya menggunakan satu langkah ke utara atau timur.
Mari kita sebut jalur seperti ini sebagai jalur yang dapat diterima jika tidak terdapat titik di ataranya yang tidak bisa diterima.
Misal P(n) adalah banyaknya jalur yang dapat diterima dari (0, 0) ke (n, n).
Dapat dibuktikan bahwa P(5) = 252, P(16) = 596994440 dan P(1000) mod 1 000 000 007 = 341920854.
Carilah P(10 000 000) mod 1 000 000 007.
Answer: 2c09e247c6144c16cae2358d316affd9
Soal 409
Misal n adalah sebuah bilangan bulat positif. Perhatikan posisi pada permainan nim dimana:
- Terdapat n buah tumpukan tidak kosong.
- Setiap tumpukan memiliki banyak batu dari 2n.
- Tidak ada dua tumpukan yang memiliki banyak batu yang sama.
Misal W(n) adalah banyaknya posisi nim kemenangan yang memenuhi kondisi di atas (sebuah posisi dimana pemain pertama akan menang). Sebagai contoh, W(1) = 1, W(2) = 6, W(3) = 168, W(5) = 19764360 dan W(100) mod 1 000 000 007 = 384777056.
Carilah W(10 000 000) mod 1 000 000 007.
Answer: 56c32e75a2656ec08ce177089bda2f53
Soal 410
Misal C adalah sebuah lingkaran dengan panjang jari-jari r, x2 + y2 = r2. Kita akan memilih dua buah titik P(a, b) dan Q(-a, c) sehingga garis yang melalui titik P dan Q merupakan garis singgung C.
Sebagai contoh, pasangan bilangan (r, a, b, c) = (2, 6, 2, -7) memenuhi sifat ini.
Misal F(R, X) adalah banyaknya pasangan bilangan bulat (r, a, b, c) yang memiliki sifat ini, dan dengan 0 < r ≤ R dan 0 < a ≤ X.
Dapat dibuktikan bahwa F(1, 5) = 10, F(2, 10) = 52 dan F(10, 100) = 3384.
Carilah F(108, 109) + F(109, 108).
Answer: 45826f3a23aa321f97acb1d2a8f2170b
Soal 411
Misal n adalah sebuah bilangan bulat positif. Akan terdapat stasiun pada koordinat (x, y) = (2i mod n, 3i mod n) untuk 0 ≤ i ≤ 2n. Kita akan menganggap stasiun yang memiliki koordinat yang sama sebagai stasiun yang sama.
Kita akan membentuk jalur dari (0, 0) ke (n, n) sehingga koordinat x dan y tidak pernah berkurang.
Misal S(n) adalah banyaknya stasiun maksimal yang dapat dilewati.
Sebagai contoh, jika n = 22, terdapat 11 buah stasiun berbeda, dan jalur yang sah sesuai dengan aturan di atas hanya dapat melewati paling banyak 5 stasiun. Sehingga, S(22) = 5. Contoh ini diilustrasikan dengan gambar berikut, dengan sebuah contoh jalur optimal:

Dapat juga dibuktikan bahwa S(123) = 14 dan S(10000) = 48.
Carilah ∑ S(k5) untuk 1 ≤ k ≤ 30.
Answer: e351762bf2220ca1396e6a9ee3f6c84f
Soal 412
Untuk bilangan bulat m, n (0 ≤ n < m), misal L(m, n) adalah sebuah kisi berukuran m×m tanpa kisi bagian kanan atas n×n.
Sebagai contoh, L(5, 3) akan terlihat seperti ini:

Kita ingin memberi nomor pada setiap sel dari L(m, n) dengan bilangan bulat berurutan 1, 2, 3, ... sehingga bilangan pada setiap sel lebih kecil daripada bilangan di sel sebelah bawah dan di sebelah kirinya.
Sebagai contoh, berikut ini adalah dua buah cara penomoran yang sah dari L(5, 3):

Misal LC(m, n) adalahnya banyak cara penomoran yang sah dari L(m, n).
Dapat dibuktikan bahwa LC(3, 0) = 42, LC(5, 3) = 250250, LC(6, 3) = 406029023400 dan LC(10, 5) mod 76543217 = 61251715.
Carilah LC(10000, 5000) mod 76543217.
Answer: 8919ccca34b7ccc293d33e06872c668d
Soal 413
Kita akan mengatakan bahwa sebuah bilangan bulat d-digit (tidak ada angka nol di depan) adalah sebuah bilangan satu anak, jika persis satu dari bilangan bagiannya (sub-string) habis dibagi oleh d.
Sebagai contoh, 5671 adalah sebuah bilangan satu anak 4-digit. Karena dari semua bilangan bagiannya 5, 6, 7, 1, 56, 67, 71, 567, 671 dan 5671, hanya 56 yang habis dibagi oleh 4 4.
Hal yang sama, 104 adalah sebuah bilangan satu anak 3-digit, karena hanya 0 yang habis dibagi oleh 3.
1132451 juga adalah bilangan satu anak 7-digit, karena hanya 245 yang habis dibagi oleh 7.
Misal F(N) adalah banyaknya bilangan satu anak kurang dari N.
Dapat dibuktikan bahwa F(10) = 9, F(103) = 389 dan F(107) = 277674.
Carilah F(1019).
Answer: 569ad33af889215704df5a9e278aa004
Soal 414
6174 adalah sebuah bilangan yang luar biasa; jika kita menyusun digit-digitnya dengan urutan menaik dan menggunakan bilangan tersebut untuk mengurangkan bilangan yang telah diurutkan secara menurun, kita dapatkan 7641-1467=6174.
Lebih luar biasanya lagi adalah, jika kita melakukan hal yang sama dengan bilangan 4 digit apapun, dan mengulang proses mengurutkan dan mengurangkan ini, suatu saat hasil perhitungan kita akan berakhir di 6174 atau langsung menjadi 0 jika semua digit adalah sama.
Ini juga berlaku dengan bilangan yang memiliki kurang dari 4 digit, jika kita mengisi bilangan tersebut dengan angka nol di depannya sampai kita memiliki bilangan 4 digit.
Sebagai contoh, mari kita mulai dengan bilangan 0837:
8730-0378=8352
8532-2358=6174
6174 disebut sebagai konstanta Kaprekar. Proses untuk mengurutkan dan mengurangkan dan mengulang-ulang proses ini sampai didapat hasil antara 0 atau konstanta Kaprekar disebut sebagai kebiasaan Kaprekar.
Kita dapat mengamati kebiasaan Kaprekar untuk bilangan dengan basis dan banyak digit lain.
Sayangnya, tidak dapat dijamin bahwa konstanta Kaprekar akan selalu ada dalam setiap kasus; proses ini dapat berakhir pada sebuah siklus untuk beberapa bilangan, atau dapat berakhir dengan bilangan konstan pada beberapa bilangan lainnya.
Tetapi, dapat ditunjukkan bahwa untuk bilangan 5 digit yang dituliskan dalam basis b = 6t+3≠9, terdapat sebuah konstanta Kaprekar.
Sebagai contoh, basis 15: (10,4,14,9,5)15
Basis 21: (14,6,20,13,7)21
Dinyatakan Cb sebagai konstanta Kaprekar pada basis b untuk bilangan 5 digit. Dinyatakan fungsi sb(i) sebagai
- 0 jika i = Cb atau jika i tertulis dalam basis b yang dibentuk dari 5 digit yang sama
- Selain itu, sb(i) dinyatakan sebagai banyaknya iterasi yang diperlukan untuk melakukan kebiasaan Kaprekar pada bilangan basis b untuk sampai pada Cb
Dinyatakan S(b) sebagai hasil penjumlahan dari sb(i) untuk 0 < i < b5.
Sehingga S(15) = 5274369
S(111) = 400668930299
Carilah hasil penjumlahan dari S(6k+3) untuk 2 ≤ k ≤ 300.
Berikan 18 digit terakhir sebagai jawaban Anda.
Answer: 42f095bdfd71e1ae4ae0ceead1bb1802
Soal 415
Sebuah himpuna dari titik dengan koordinat bilangan bulat S disebut sebagai sebuah himpunan titanic jika terdapat sebuah garis melalui persis hanya dua buah titik pada S.
Sebuah contoh dari sebuah himpunan titanic adalah S = {(0, 0), (0, 1), (0, 2), (1, 1), (2, 0), (1, 0)}, dimana garis yang ada akan melalui (0, 1) dan (2, 0), dan tidak akan melalui titk lain pada S.
Sedangkan, himpunan {(0, 0), (1, 1), (2, 2), (4, 4)} bukanlah merupakan himpunan titanic, karena garis yang melalui dua buah titik juga melalui titik lainnya pada himpunan ini.
Untuk setiap bilangan bulat positif N, misal T(N) adalah banyaknya himpunan titanic S, dimana setiap titik (x, y) memenuhi 0 ≤ x, y ≤ N. Dapat dibuktikan bahwa T(1) = 11, T(2) = 494, T(4) = 33554178, T(111) mod 108 = 13500401 dan T(105) mod 108 = 63259062.
Carilah T(1011) mod 108.
Answer: 2357ad217832274f444cae2a6580b193
Soal 416
Pada sebuah baris berisi n buah persegi, terdapat seekor katak di persegi yang paling kiri. Secara berturut-turut katak tersebut akan melompat menuju persegi yang paling kanan, dan kemudian kembali ke persegi paling kiri. Pada saat perjalanan pergi, ia akan melompat sebanyak satu, dua atau tiga buah persegi ke kanan, dan pada perjalanan pulang, ia akan melompat ke kiri dengan cara yang sama. Ia tidak dapat mendarat keluar dari persegi. Ia mengulangi perjalanan bolak balik sebanyak m kali.
Misal F(m, n) adalah banyaknya cara sang katak dapat berpindah, sehingga paling banyak hanya ada satu persegi yang masih belum pernah ditempati sang katak.
Sebagai contoh, F(1, 3) = 4, F(1, 4) = 15, F(1, 5) = 46, F(2, 3) = 16 dan F(2, 100) mod 109 = 429619151.
Carilah 9 digit terakhir dari F(10, 1012).
Answer: 6f398386fdfec57ac166d4970c2bcad2
Soal 417
Sebuah unit pecahan adalah sebuah pecahan yang memiliki pembilang 1. Representasi desimal dari unit pecahan untuk penyebut dari 2 sampai 10 adalah sebagai berikut:
1/2 = 0.5 1/3 = 0.(3) 1/4 = 0.25 1/5 = 0.2 1/6 = 0.1(6) 1/7 = 0.(142857) 1/8 = 0.125 1/9 = 0.(1) 1/10 = 0.1
Dimana 0.1(6) berarti 0.166666..., dan memiliki 1 digit yang berulang. Dapat kita lihat bahwa 1/7 memiliki 6 digit yang berulang.
Unit pecahan yang penyebutnya tidak memiliki faktor prima selain 2 dan/atau 5 dianggap tidak memiliki digit berulang.
Kita akan menyatakan panajng dari digit berulang untuk unit pecahan tersebut adalah 0.
Misal L(n) menyatakan panjang dari digit berulang untuk 1/n. Diketahui bahwa ∑L(n) untuk 3 ≤ n ≤ 1 000 000 sama dengan 55535191115.
Carilah ∑L(n) untuk 3 ≤ n ≤ 100 000 000
Answer: 93a7df08c972f1e7788516d056a7e016
Soal 418
Misal n adalah sebuah bilangan bulat positif. Sebuah kumpulan bilangan bulat (a, b, c) disebut sebagai sebuah tripel faktorisasi dari n jika:
- 1 ≤ a ≤ b ≤ c
- a·b·c = n.
Dinyatakan f(n) sebagai a + b + c untuk tripel faktorisasi (a, b, c) dari n yang memiliki nilai c / a paling sederhana. Dapat ditunjukkan bahwa kumpulan bilangan ini adalah unik.
Sebagai contoh, f(165) = 19, f(100100) = 142 dan f(20!) = 4034872.
Carilah f(43!).
Answer: b032468ddb4847d8a2273789379753f5
Soal 419
Barisan Lihat dan sebut adalah 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ...
Barisan ini dimulai dengan bilangan 1, dan orang lain yang ada menjelaskan banyaknya bilangan yang sama dari bilangan yang diucapkan oleh orang sebelumnya.
Akan menolong apabila hal ini dilakukan dengan berbicara:
1 adalah 'satu buah satu' → 11
11 adalah 'dua buah satu' → 21
21 adalah 'satu buah dua dan satu buah satu' → 1211
1211 adalah 'satu buah satu, satu buah dua dan dua buah satu' → 111221
111221 adalah 'tiga buah satu, dua buah dua dan satu buah satu' → 312211
...
Dinyatakan A(n), B(n) dan C(n) secara berurutan sebagai banyaknya angka satu, dua dan tiga pada suku ke-n dari barisan ini.
Dapat dibuktikan bahwa A(40) = 31254, B(40) = 20259 dan C(40) = 11625.
Carilah A(n), B(n) dan C(n) untuk n = 1012.
Berikan jawaban Anda yang telah di modulo 230, dan pisahkan nilai untuk A, B dan C dengan sebuah tanda koma.
Sebagai contoh, untuk n = 40 jawabannya akan menjadi 31254,20259,11625
Answer: b27db655498b3d64ad4338fcdc9d178f
Soal 420
Sebuah matriks bilangan bulat positif adalah sebuah matriks yang semua elemennya adalah bilangan bulat positif.
Beberapa matriks bilangan bulat positif dapat diekspresikan sebagai hasil kuadrat dari matriks bilangan bulat positif lain dengan dua cara yang berbeda. Berikut ini adalah contohnya:

Kita nyatakan F(N) sebagai banyaknya matriks bilangan bulat positif 2x2, dimana memiliki hasil jumlah diagonal utama (trace) kurang dari N dan dapat dinyatakan sebagai hasil kuadrat dari matriks bilangan bulat positif lain dengan dua cara yang berbeda.
Dapat dibuktikan bahwa F(50) = 7 dan F(1000) = 1019.
Carilah F(107).
Answer: e265e34e34fc54e8ceecd5e4b94b1381
Soal 421
Bilangan dalam bentuk n15+1 adalah merupakan bilangan komposit untuk setiap bilangan bulat n > 1.
Untuk bilangan bulat positif n dan m misal s(n,m) dinyatakan sebagai hasil penjumlahan dari faktor prima berbeda dari n15+1 yang tidak melebihi m.
Sebagai contoh 215+1 = 3×3×11×331.
Sehingga s(2,10) = 3 dan s(2,1000) = 3+11+331 = 345.
Juga 1015+1 = 7×11×13×211×241×2161×9091.
Sehingga s(10,100) = 31 dan s(10,1000) = 483.
</P>
Carilah ∑ s(n,108) untuk 1 ≤ n ≤ 1011.
Answer: 481fcc5ff16ccf1645fb136c123ed660
Soal 422
Misal H adalah hiperbola yang dinyatakan dengan persamaan 12x2 + 7xy - 12y2 = 625.
Kemudian, dinyatakan X sebagai titik (7, 1). Dapat terlihat bahwa X berada pada H.
Sekarang kita akan menyatakan sebuah barisan dari titik-titik di H, {Pi : i ≥ 1}, sebagai:
- P1 = (13, 61/4).
- P2 = (-43/6, -4).
- Untuk i > 2, Pi adalah titik unik pada H yang berbeda dari Pi-1 dan garis PiPi-1 adalah sejajar dengan garis Pi-2X. Dapat ditunjukkan bahwa Pi selalu dapat terdefinisi, dan koordinatnya selalu rasional.

Anda diberikan informasi bahwa P3 = (-19/2, -229/24), P4 = (1267/144, -37/12) dan P7 = (17194218091/143327232, 274748766781/1719926784).
Carilah Pn untuk n = 1114 dalam format berikut ini:
If Pn = (a/b, c/d) dimana pecahan yang ada sudah dalam bentuk paling sederhana, dan penyebutnya adalah positif, maka jawaban yang diberikan adalah (a + b + c + d) mod 1 000 000 007.
Untuk n = 7, jawabannya akan menjadi: 806236837.
Answer: 7034610688a8851f742f912143c1becf
Soal 423
Misal n adalah bilangan bulat positif.
Sebuah dadu bersisi 6 dilempar sebanyak n kali. Misal c adalah banyaknya pasangan dua lemparan berurutan yang mengeluarkan angka dadu yang sama.
Sebagai contoh, jika n = 7 dan hasil lemparan dadunya adalah (1,1,5,6,6,6,3), maka pasangan-pasangan berikut ini memiliki angka dadu yang sama:
(1,1,5,6,6,6,3)
(1,1,5,6,6,6,3)
(1,1,5,6,6,6,3)
Sehingga, c = 3 untuk (1,1,5,6,6,6,3).
Dinyatakan C(n) sebagai banyaknya hasil yang mungkin saat melempar dadu bersisi 6 sebanyak n kali, sehingga c tidak melebihi π(n).1
Sebagai contoh, C(3) = 216, C(4) = 1290, C(11) = 361912500 dan C(24) = 4727547363281250000.
Dinyatakan S(L) sebagai ∑ C(n) untuk 1 ≤ n ≤ L.
Sebagai contoh, S(50) mod 1 000 000 007 = 832833871.
Carilah S(50 000 000) mod 1 000 000 007.
1 π melambangkan fungsi menghitung banyaknya prima, sehingga π(n) adalah banyaknya bilangan prima ≤ n.
Answer: e2add9d46ebd8ba59a07dca791cd629b
Soal 424

Gambar di atas adalah sebuah contoh dari teka-teki kakuro rahasia (juga dikenal sebagai penjumlahan menyilang, atau penyilangan jumlah genap), dengan solusi akhirnya ada di sebelah kanan. (Aturan yang biasa digunakan pada teka-teki kakuro dapat dengan mudah ditemukan di banyak situs internet. Informasi lainnya yang berhubungan saat ini juga dapat ditemukan di krazydad.com dimana penulisnya telah memberikan data teka-teki untuk tantangan ini.)
Sebuah text file yang dapat di download ([kakuro200.txt](/projecteuler/files/kakuro200.txt)) berisi deskripsi dari 200 teka-teki seperti ini, gabungan dari tipe 5x5 dan 6x6. Teka-teki pertama pada file ini adalah contoh di atas, yang dituliskan sebagai berikut:
6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X
Karakter pertama adalah digit numerik yang menandakan ukuran dari kotak-kotak. Digit ini dapat memiliki nilai 6 (untuk sebuah teka-teki kakuro 5x5) atau nilai 7 (untuk teka-teki 6x6) diikuti oleh tanda koma (,). Kelebihan satu baris di atas dan di kiri diperlukan untuk memasukkan informasi.
Isi dari setiap sel kemudian dijelaskan dan diikuti oleh tanda koma, dari kiri ke kanan dan dimulai dari baris atas.
X = Sel abu-abu, tidak perlu diisi oleh digit.
O (huruf kapital)= Sel putih kosong yang akan diisi oleh digit.
A = Atau sel lain yang terdapat huruf kapital dari A sampai J harus diganti dengan digit yang ekuivalen untuk mendapatkan jawaban teka-teki.
( ) = Lokasi dari hasil penjumlahan rahasia. Penjumlahan horizontal di diawali dengan huruf "h" kecil, dan penjumlahan vertikal diawali dengan huruf "v" kecil. Kemudian huruf tersebut diikuti oleh satu atau dua huruf kapital tergantuk dari hasil penjumlahannya, apakah satu digit atau dua gitig. Untuk hasil penjumlahan dua digit, huruf pertama merupakan "puluhan" dan huruf kedua merupakan "satuan". Saat sel harus berisi informasi baik untuk penjumlahan horizontal maupun vertikal, maka bagian yang pertama selalu merupakan penjumlahan untuk horizontal, dan keduanya dipisahkan dengan sebuah tanda koma di dalam kurung yang sama, contoh: (hFE,vD). Setiap set tanda kurung juga langsung diikuti oleh tanda koma.
Deskripsi dari sel terakhir tidak diikuti oleh tanda koma, melainkan akan diikuti oleh Carriage Return/Line Feed (CRLF).
Jawaban yang diperlukan untuk setiap teka-teki didasarkan pada nilai dari setiap huruf yang diperlukan untuk sampai kepada solusi, dan bedasarkan urutan abjad. Seperti yang ditunjukkan pada contoh teka-teki, jawabannya adalah 8426039571. Setidaknya 9 dari 10 huruf rahasia akan selalu menjadi bagian dari deskripsi masalah. Saat hanya 9 yang diberikan, satu yang masih belum ditemukan harus diberikan digit yang masih tersisa.
Anda diberikan informasi bahwa hasil penjumlahan dari jawaban untuk 10 teka-teki pertama pada file adalah 64414157580.
Carilah hasil penjumlahan untuk ke 200 buah teka-teki.
Answer: c412afe5b5d76dbfbb77443ed5836d89
Soal 425
Dua bilangan positif A dan B dapat dikatakan terkoneksi (dilambangkan dengan "A ↔ B") jika satu dari kondisi-kondisi ini terpenuhi:
(1) A dan B memiliki panjang bilangan yang sama dan hanya memiliki perbedaan satu digit; sebagai contoh, 123 ↔ 173.
(2) Menambahkan satu digit di sebelah kiri A (atau B) akan menghasilkan bilangan yang sama dengan B (atau A); sebagai contoh, 23 ↔ 223 and 123 ↔ 23.
Kita menyebut sebuah bilangan prima P sebagai relatif ke-2 jika terdapat sebuah rantai dari bilangan-bilangan prima yang terkoneksi antara 2 dan P, dan tidak ada bilangan prima pada rantai yang melebihi P.
Sebagai contoh, 127 adalah relatif ke-2. Satu dari kemungkinan rantai yang ada ditunjukkan sebagai berikut:
2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127
Tetapi, 11 dan 103 bukanlah bilangan relatif ke-2.
Misal F(N) adalah hasil penjumlahan dari bilangan prima ≤ N yang bukan merupakan bilangan relatif ke-2.
Dapat dibuktikan bahwa F(103) = 431 dan F(104) = 78728.
Carilah F(107).
Answer: 3d229894ba4c585138125e802af2d06e
Soal 426
Terdapat sebanyak tak hingga baris peti. Beberapa dari peti berisi bola. Sebagai contoh, sebuah konfigurasi awal dari 2 peti berurutan yang telah terisi diikuti oleh 2 peti kosong, 2 peti terisi, 1 peti kosong, dan 2 peti terisi, dapat dituliskan dalam barisan (2, 2, 2, 1, 2), dimana banyaknya peti yang terisi dan kosong muncul secara bergantian.
Sebuah perubahan dilakukan dengan cara memindahkan setiap bola persis sekali bedasarkan aturan berikut: Pindahkan bola yang ada di paling kiri yang belum dipindahkan ke peti kosong terdekat di sebelah kanannya.
Setelah satu kali perubahan, barisan (2, 2, 2, 1, 2) berubah menjadi (2, 2, 1, 2, 3) seperti dapat dilihat pada gambar berikut; perlu diingat bahwa awal dari barisan selalu dimulai dari banyaknya peti yang telah terisi.

Sistem seperti ini disebut sebagai sebuah Sistem Bola Peti (Box-Ball System) atau dapat disingkat BBS.
Dapat ditunjukkan bahwa setelah dilakukan beberapa kali perubahan, sistem akan ada pada satu kondisi dimana banyaknya peti yang ditempati tidak akan berubah lagi pada putaran selanjutnya. Pada contoh berikut ini, bilangan berurutan yang menyatakan banyaknya peti yang ditempati adalah [1, 2, 3]; kita akan menyebut ini sebagai kondisi akhir.
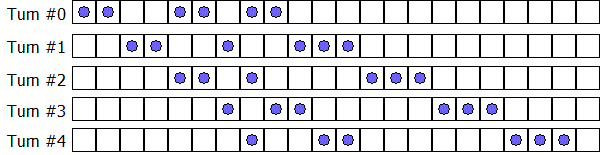
Kita nyatakan barisan {ti}:
- s0 = 290797
- sk+1 = sk2 mod 50515093
- tk = (sk mod 64) + 1
Dimulai dari konfigurasi awal (t0, t1, …, t10), kondisi akhirnya akan menjadi [1, 3, 10, 24, 51, 75].
Dimulai dari kondisi awal (t0, t1, …, t10 000 000), carilah kondisi akhirnya.
Berikan jawaban Anda dalam bentuk penjumlahan hasil kuadrat elemen-elemen pada kondisi akhir. Sebagai contoh, jika kondisi akhirnya adalah [1, 2, 3] maka 14 ( = 12 + 22 + 32) adalah jawaban Anda.
Answer: b5d8157a351482da47da0512ca374007
Soal 427
Sebuah barisan bilangan bulat S = {si} disebut sebagai sebuah barisan-n jika barisan ini mempunyai n buah elemen, dan setiap elemen si memenuhi 1 ≤ si ≤ n. Sehingga terdapat sebanyak nn buah barisan-n berbeda. Sebagai contoh, barisan S = {1, 5, 5, 10, 7, 7, 7, 2, 3, 7} adalah sebuah barisan-10.
Untuk setiap barisan S, misal L(S) adalah panjang dari sub-barisan terpanjang dari S yang memiliki nilai yang sama. Sebagai contoh, untuk barisan S di atas, L(S) = 3, karena terdapat tiga buah angka 7 yang berurutan.
Misal f(n) = ∑ L(S) untuk semua barisan-n S.
Sebagai contoh, f(3) = 45, f(7) = 1403689 dan f(11) = 481496895121.
Carilah f(7 500 000) mod 1 000 000 009.
Answer: ecb4da2c940b517c63d8d256814dd511
Soal 428
Misal a, b dan c adalah bilangan positif.
Misal W, X, Y, Z adalah empat buah titik kolinear dimana |WX| = a, |XY| = b, |YZ| = c dan |WZ| = a + b + c.
Misal Cin adalah lingkaran yang memiliki panjang diameter XY.
Misal Cout adalah lingkaran yang memiliki panjang diameter WZ.
Kumpulan bilangan (a, b, c) akan disebut sebagai sebuah tripel kalung jika Anda dapat meletakkan k ≥ 3 lingkaran berbeda C1, C2, ..., Ck sehingga:
- Ci tidak memiliki titik dalam lingkaran yang sama dengan lingkaran Cj untuk 1 ≤ i, j ≤ k dan i ≠ j,
- Ci menyinggung lingkaran Cin dan Cout untuk 1 ≤ i ≤ k,
- Ci menyinggung lingkaran Ci+1 untuk 1 ≤ i < k, dan
- Ck menyinggung lingkaran C1.
Sebagai contoh, (5, 5, 5) dan (4, 3, 21) adalah tripel kalung, sementara dapat ditunjukkan bahwa (2, 2, 5) adalah bukan tripel kalung.

Misal T(n) adalah banyaknya tripel kalung (a, b, c) sehingga a, b dan c adalah bilangan bulat positif, dan b ≤ n. Sebagai contoh, T(1) = 9, T(20) = 732 dan T(3000) = 438106.
Carilah T(1 000 000 000).
Answer: c6010c109b66b34bf3594e63eb58b446
Soal 429
Sebuah kesatuan faktor d dari suatu bilangan n adalah sebuah faktor dari n yang mempunyai sifat FPB(d, n/d) = 1.
Kesatuan faktor dari 4! = 24 adalah 1, 3, 8 dan 24.
Hasil penjumlahan dari kuadrat bilangan-bilangan tersebut adalah 12 + 32 + 82 + 242 = 650.
Misal S(n) melambangkan hasil penjumlahan dari kuadrat bilangan-bilangan kesatuan faktor dari n. Maka S(4!)=650.
Carilah S(100 000 000!) modulo 1 000 000 009.
Answer: ec4f87b0c01680e951326d9e85d2c03f
Soal 430
N buah disk diletakkan pada suatu baris, dan diberi nomor dari 1 hingga N dari kiri ke kanan.
Setiap disk memiliki sisi bewarna hitam dan sisi bewarna putih. Mula-mulanya, semua disk menunjukkan sisi mereka yang bewarna putih.
Pada setiap giliran, two buah bilangan bulat A dan B yang tidak harus berbeda antara 1 dan N (1 dan N juga termasuk) dipilih secara acak.
Semua disk dengan nomor dari A sampai B (A dan B juga termasuk) dibalik.
Contoh berikut ini menunjukkan kasus N = 8. Pada giliran pertama A = 5 dan B = 2, dan pada giliran ke dua A = dan and B = 6.

Misal E(N, M) adalah nilai harapan (expected number) dari disk yang akan menunjukkan sisi bewarna putih setelah M kali giliran.
Dapat dibuktikan bahwa E(3, 1) = 10/9, E(3, 2) = 5/3, E(10, 4) ≈ 5.157 dan E(100, 10) ≈ 51.893.
Carilah E(1010, 4000).
Berikan jawaban Anda yang telah dibulatkan hingga 2 angka di belakang koma.
Answer: 32b0825d7a110a1a220e80629c413411
Soal 431
Fred adalah seorang petani, dan ia sedang mengatur silo baru yang akan dipasang di ladangnya, ia memiliki obsesi untuk mempunyai semua benda yang berbentuk persegi, ia akan sangat marah apabila ia melihat sesuatu yang berbentuk melingkar. Quentin sebagai perwakilan dari perusahaan yang akan memasang silo menjelaskan bahwa mereka hanya membuat silo berbentuk silinder, namun ia mengatakan bahwa silo ini dapat diletakkan pada alas berbentuk persegi. Fred tidak puas dan memaksa silo ini disingkirkan dari ladangnya.
Dengan berpikir cepat Quentin menjelaskan bahwa saat butiran beras/gandum dimasukkan dari atas, akan terbentuk bentuk landai seperti kerucut, dan akan terbentuk sudut alami dengan bidang horizontal yang disebut sebagai sudut repose. Sebagai contoh, jika sudut repose, $\alpha = 30$ derajat, dan butiran beras/gandum dimasukkan dari tengah silo, maka akan terbentuk kerucut sempurna yang mengarah ke sebelah atas silinder. Jika pada silo ini, yang memiliki panjang diameter 6m, banyaknya ruang yang tidak dapat digunakan diperkirakan sekitar 32.648388556 m3. Tetapi, apabila butiran beras/gandum dimasukkan pada satu titik di bagian atas, yang memiliki jarak horizontal $x$ meter dari pusat, maka kerucut yang ada dengan aneh akan membentuk kurva dan akan terbentuk daerah miring. Ia menunjukkan kepada fred sebuah gambar.
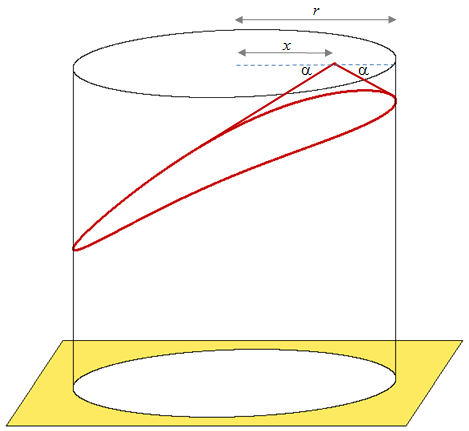
Kita akan menentukan banyaknya bagian yang tidak terpakai dalam meter kubik yang diberikan oleh $V(x)$. Jika $x = 1.114785284$, dimana merupakan bilangan tiga kuadrat angka di belakang koma, maka banyaknya ruang yang tidak terpakai, $V(1.114785284) \approx 36$. Masih terdapat persis satu buah solusi lain untuk permasalahan ini: $V(2.511167869) \approx 49$. Ini akan seperti mengetahui bahwa bilangan persegi/kuadrat merupakan raja dari silo, duduk dengan kejayaannya di atas butiran beras/gandum anda.
Mata Fred berbinar-binar saat mendengar resolusi elegan ini, namun dengan mengamati secara teliti dari gambar Quentin dan hasil perhitungannya, kebahagiaannya berubah menjadi kemurungan sekali lagi. Fred mengemukakan kepada Quentin bahwa panajng jari-jari silo yang seharusnya 6 meter, bukan diameternya, dan sudut kemiringan dari butiran beras/gandumnya adalah 40 derajat. Tetapi, apabila Quentin dapat menemukan suatu set solusi untuk silo seperti ini, maka ia akan menjadi lebih senang untuk tetap mempertahankan silo ini dari ladangnya.
Jika pemikiran cepat Quentin dapat memuaskan seorang yang frustasi dan rewel, yaitu Fred sang petani yang ingin segala sesuatunya persegi, maka carilah nilai dari $x$ untuk semua kemungkinan banyaknya volume silo yang tidak dapat digunakan dalam bentuk bilangan persegi/kuadrat dan hitunglah $\sum x$ dibulatkan hingga 9 angka di belakang koma.
Answer: 5e5d81aa8bfaf92f68cdef0154c5c238
Soal 432
Misal S(n,m) = ∑φ(n × i) untuk 1 ≤ i ≤ m. (φ adalah fungsi totient Euler)
Diketahui S(510510,106 )= 45480596821125120.
Carilah S(510510,1011).
Berikan 9 digit terakhir dari jawaban Anda.
Answer: e171c2872d650e47589842faa80f5707
Soal 433
Misal E(x0, y0) adalah banyaknya langkah yang diperlukan untuk menentukan faktor persekutuan terbesar dari x0 dan y0 dengan algoritma Euclid. Atau secara lebih formal:
x1 = y0, y1 = x0 mod y0
xn = yn-1, yn = xn-1 mod yn-1
E(x0, y0) adalah nilai n terkecil sehingga yn = 0.
Kita dapatkan E(1,1) = 1, E(10,6) = 3 dan E(6,10) = 4.
Dinyatakan S(N) sebagai hasil penjumlahan dari E(x,y) untuk 1 ≤ x,y ≤ N.
Kita dapatkan S(1) = 1, S(10) = 221 dan S(100) = 39826.
Carilah S(5·106).
Answer: 0eeca9fa5cf25a2bfae01f1f04d6cd35
Soal 434
Grafik adalah kumpulan dari beberapa titik dan garis penghubung, dan dua buah titik yang dihubungkan oleh sebuah garis disebut bersebelahan.
Grafik dapat digambarkan pada ruang Euclidean dengan menghubungkan setiap titik pada grafik dengan titik pada ruang euclidean.
Sebuah grafik fleksibel adalah proses penggambaran sebuah grafik, dimana memungkinkan untuk menggeser satu atau lebih titik secara terus menerus, sehingga jarak antara dua titik yang tidak bersebelahan dapat berubah, sementara jarak antara dua titik yang bersebelahan dijaga tetap konstan.
Sebuah grafik kaku adalah proses penggambaran sebuah grafik yang tidak fleksibel.
Atau secara tidak formal, sebuah grafik disebut kaku jika titik-titik pada grafik diganti dengan sebuah engsel yang dapat berputar, dan garis-garis pada grafik diganti dengan tiang yang tidak dapat bengkok dan tidak elastis, tidak ada bagian pada grafik yang dapat bergerak sendiri tanpa mengubah bagian lain dari grafik.
Grafik kotak-kotak yang digambar pada ruang Euclidean adalah tidak kaku, seperti yang dicontohkan oleh animasi berikut:

Tetapi, salah satu cara untuk dapat menjadikan grafik tersebut kaku adalah dengan menambahkan garis diagonal pada setiap kotak. Sebagai contoh, untuk grafik kotak-kotak berukuran 2x3, terdapat 19 cara untuk menjadikan grafik kaku:

Perlu di ingat tujuan dari permasalahan ini, kita tidak menganggap perubahan arah dari garis diagonal atau menambahkan dua buah diagonal pada satu kotak sebagai cara yang berbeda untuk membuat grafik menjadi kaku.
Misal R(m,n) adalah banyaknya cara untuk membuat grafik kotak-kotak berukuran m × n menjadi kaku.
Sebagai contoh, R(2,3) = 19 dan R(5,5) = 23679901
Dinyatakan S(N) sebagai ∑R(i,j) untuk 1 ≤ i, j ≤ N.
Sehingga S(5) = 25021721.
Carilah S(100), berikan jawaban Anda yang telah di modulo 1000000033
Answer: f51d9fd41a8ce217682321a020be6fec
Soal 435
Bilangan Fibonacci {fn, n ≥ 0} dinyatakan secara rekursif sebagai fn = fn-1 + fn-2 dengan basis f0 = 0 dan f1 = 1.
Dinyatakan polinomial {Fn, n ≥ 0} sebagai Fn(x) = ∑fixi untuk 0 ≤ i ≤ n.
Sebagai contoh, F7(x) = x + x2 + 2x3 + 3x4 + 5x5 + 8x6 + 13x7, dan F7(11) = 268357683.
Misal n = 1015. Carilah hasil penjumlahan [∑0≤x≤100 Fn(x)] mod 1307674368000 (= 15!).
Answer: 0f08231a97e872f565a085de75743a1c
Soal 436
Julie menawarkan taruhan berikut ini ke adiknya Louise.
Ia menawarkan sebuah permainan peluang untuk menentukan siapa yang akan mencuci piring.
Untuk permainan ini, mereka harus menggunakan pembuat bilangan acak yang memiliki sebaran uniform antara 0 dan 1.
Permainan dimulai dengan S = 0.
Pemain pertama, yaitu Louise, menambahkkan ke S angka acak berbeda dari pembuat bilangan acak sampai S > 1 dan ia mencatat angka acak terakhir 'x'.
Pemain kedua, yaitu Julie, melanjutkan menambahkan ke S angka acak berbeda dari pembuat bilangan acak sampai S > 2 dan mencatat angka acak terakhir 'y'.
Pemain yang memiliki angka tertinggi adalah pemenangnya dan yang kalah akan mencuci piring, sehingga apabila y > x pemain kedua akan menang.
Sebagai contoh, jika pemain pertama mendapatkan angka 0.62 dan 0.44, maka giliran pemain pertama akan selesai, karena 0.62+0.44 > 1 dan x = 0.44.
Kemudian jika pemain kedua mendapatkan angka 0.1, 0.27 dan 0.91, giliran pemain kedua akan berakhir, karena 0.62+0.44+0.1+0.27+0.91 > 2 dan y = 0.91.
Karena y > x, paka pemain kedua akan menang.
Louise memikirkan permainan ini sejenak, dan mengatakan: "Itu tidak adil".
Berapakah peluang pemain kedua akan menang?
Berikan jawaban Anda dibulatkan hingga 10 angka di belakang koma dengan format 0.abcdefghij
Answer: d797ed72189f045e8ea48aa960fec1f3
Soal 437
Saat kita menghitung 8n modulo 11 untuk n=0 sampai 9, kita dapatkan: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
Seperti yang kita lihat, semua angka dari 1 sampai 10 muncul. Sehingga 8 adalah akar primitif dari 11.
Tetapi terdapat satu hal lagi:
Jika kita mengamati dengan lebih teliti, kita dapat melihat bahwa:
1+8=9
8+9=17≡6 mod 11
9+6=15≡4 mod 11
6+4=10
4+10=14≡3 mod 11
10+3=13≡2 mod 11
3+2=5
2+5=7
5+7=12≡1 mod 11.
Sehingga bilangan pangkat 8 mod 11 adalah bilangan siklik dengan periode 10, dan 8n + 8n+1 ≡ 8n+2 (mod 11).
8 sekarang akan disebut sebagai akar primitif Fibonacci dari 11.
Tidak semua bilangan prima memiliki akar primitif Fibonacci.
Terdapat 323 buah bilangan prima kurang dari 10000 yang memiliki satu atau lebih akar primitif Fibonacci, dan hasil penjumlahan dari bilangan prima tersebut adalah 1480491.
Carilah hasil penjumlahan bilangan prima kurang dari 100,000,000 yang memiliki setidaknya satu buah akar primitif Fibonacci.
</P>
Answer: 98bb66462d635d8225416a644e4637b0
Soal 438
Untuk n-buah bilangan bulat t = (a1, ..., an), misal (x1, ..., xn) adalah solusi dari persamaan polinomial xn + a1xn-1 + a2xn-2 + ... + an-1x + an = 0.
Terdapat dua buah kondisi:
- x1, ..., xn semuanya adalah bilangan real.
- Jika x1, ..., xn adalah berurutan, ⌊xi⌋ = i untuk 1 ≤ i ≤ n. (⌊·⌋: fungsi pembulatan ke bawah.)
Pada kasus n = 4, terdapat 12 buah kumpulan n-buah bilangan bulat yang memenuhi kedua kondisi tersebut.
Kita nyatakan S(t) sebagai hasil penjumlahan dari nilai mutlak bilangan bulat pada t.
Untuk n = 4 dapat dibuktikan bahwa ∑S(t) = 2087 untuk semua n-buah bilangan t yang memenuhi kedua kondisi tersebut.
Carilah ∑S(t) untuk n = 7.
Answer: ff0c265a14c2c0bb56f10dbff1768338
Soal 439
Misal d(k) adalah hasil penjumlahan semua faktor dari k.
Kita nyatakan fungsi S(N) = ∑1≤i≤N ∑1≤j≤N d(i·j).
Sebagai contoh, S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59.
Diketahui S(103) = 563576517282 dan S(105) mod 109 = 215766508.
Carilah S(1011) mod 109.
Answer: da937ac1432c8ccd4de6f68df36e7980
Soal 440
Kita akan memasang ubin pada sebuah papan dengan panjang n dan tinggi 1 sampai semua bagian tertutupi, dengan blok ubin berukuran 1 × 2 atau 1 × 1, yang memiliki satu digit desimal di atasnya:

Sebagai contoh, berikut ini adalah beberapa cara untuk memasang ubin pada papan dengan panjang n = 8:

Misal T(n) adalah banyaknya cara untuk memasang ubin pada papan dengan panjang n seperti dijelaskan di atas.
Sebagai contoh, T(1) = 10 dan T(2) = 101.
Misal S(L) adalah hasil penjumlahan ∑a,b,c fpb(T(ca), T(cb)) untuk 1 ≤ a, b, c ≤ L.
Sebagai contoh:
S(2) = 10444
S(3) = 1292115238446807016106539989
S(4) mod 987 898 789 = 670616280.
Carilah S(2000) mod 987 898 789.
Answer: 214573d310bf2f02e066e4a9c193cc23
Soal 441
Untuk sebuah bilangan bulat M, dinyatakan R(M) sebagai hasil penjumlahan dari 1/(p·q) untuk semua pasangan bilangan bulat p dan q yang memenuhi semua kondisi berikut ini:
- 1 ≤ p < q ≤ M
- p + q ≥ M
- p dan q adalah koprima.
Kita juga akan menyatakan S(N) sebagai hasil penjumlahan dari R(i) untuk 2 ≤ i ≤ N.
Dapat juga dibuktikan bahwa S(2) = R(2) = 1/2, S(10) ≈ 6.9147 dan S(100) ≈ 58.2962.
Carilah S(107). Berikan jawaban Anda dibulatkan hingga empat angka di belakang koma.
Answer: 152cc265f5461c5055db95a122280416
Soal 442
Sebuah bilangan bulat dikatakan sebagai bebas sebelas apabila pada angka-angkanya tidak terdapat bilangan yang merupakan hasil 11 pangkat suatu angka kecuali angka 1 (110).
Sebagai contoh, 2404 dan 13431 adalah bilangan bebas sebelas, sedangkan 911 dan 4121331 adalah bukan.
Misal E(n) adalah bilangan bulat positif bebas sebelas pada urutan ke-n. Sebagai contoh, E(3) = 3, E(200) = 213 dan E(500 000) = 531563.
Carilah E(1018).
Answer: c31bb13db787bce9a169dce600aec863
Soal 443
Misal g(n) adalah barisan yang dinyatakan sebagai berikut:
g(4) = 13,
g(n) = g(n-1) + fpb(n, g(n-1)) untuk n > 4.
Beberapa nilai pertamanya adalah:
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ... |
| g(n) | 13 | 14 | 16 | 17 | 18 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 51 | 54 | 55 | 60 | ... |
Diketahui g(1 000) = 2524 dan g(1 000 000) = 2624152.
Carilah g(1015).
Answer: 28f9d9a9bf8fb3d606e0b711b59f42aa
Soal 444
Sebuah kelompok berisi p orang memutuskan untuk duduk pada sebuah meja bundar dan memainkan sebuah permainan pertukaran tiket lotere. Setiap orang memulai dengan tiket lotere yang masih mulus yang diberikan secara acak. Setiap tiket, saat digosok, akan menunjukkan hadiah uang antara £1 sampai £p, dan tidak terdapat dua tiket yang memiliki hadiah yang sama. Tujuan dari permainan ini untuk setiap orang adalah untuk mendapatkan tiket dengan hadiah terbesar begitu permainan berakhir.
Satu orang ditunjuk secara acak untuk menjadi pemain pertama. Dengan memutari sekeliling meja, setiap orang hanya dapat memilih satu dari dua pilihan:
1. Pemain dapat menggosok tiketnya dan memberitahukan besar hadiah yang didapatkan kepada semua orang di meja.
2. Pemain dapat menukarkan tiketnya yang masih mulus dengan tiket pemain sebelumnya yang telah digosok, dan kemudian pergi dengan membawa tiket tersebut. Pemain sebelumnya yang mendapatkan tiket baru kemudian menggosok tiketnya dan memberitahukan besar hadiah yang didapatkan kepada semua orang yang ada di meja.
Permainan berakhir saat semua tiket telah digosok. Semua pemain yang masih ada di meja harus pergi dengan membawa tiket yang ada di tangannya.
Asumsikan setiap pemain menggunakan strategi optimal untuk mendapatkan nilai harapan (expected value) terbesar dari hadiah yang didapatkan oleh tiketnya.
Misal E(p) menyatakan dugaan banyaknya (expected number) pemain yang meninggalkan meja saat permainan berakhir, pada permainan yang dimainkan oleh p orang (Sebagai contoh E(111) = 5.2912 saat dibulatkan hingga 5 angka).
Misal S1(N) =  E(p)
E(p)
Misal Sk(N) =  Sk-1(p) untuk k > 1
Sk-1(p) untuk k > 1
Carilah S20(1014) dan tuliskan jawaban Anda sesuai dengan aturan notasi ilmiah, dibulatkan hingga 10 angka. Gunakan huruf kecil untuk memisahkan mantissa dan eksponen (Sebagai contoh S3(100) = 5.983679014e5).
Answer: e6745c386ba3c0de1bf56897e453c7c8
Soal 445
Untuk setiap bilangan bulat n>1, dinyatakan sebuah fungsi fn,a,b dengan fn,a,b(x)≡ax+b mod n untuk a,b,x bilangan bulat dan 0<a<n, 0≤b<n, 0≤x<n.
Kita akan menyebutr fn,a,b sebagai sebuah retraksi apabila fn,a,b(fn,a,b(x))≡fn,a,b(x) mod n untuk setiap 0≤x<n.
Misal R(n) adalah banyaknya retraksi untuk n.
Anda diberikan informasi bahwa
∑ R(c) untuk c=C(100 000,k), dan 1 ≤ k ≤99 999 ≡628701600 (mod 1 000 000 007).
(C(n,k) adalah koefisien binomial).
Carilah ∑ R(c) untuk c=C(10 000 000,k), dan 1 ≤k≤ 9 999 999.
Berikan jawaban Anda yang telah di modulo 1 000 000 007.
Answer: 0183cdbc44f24e971bd824e9deb2b478
Soal 446
Untuk setiap bilangan bulat n>1, dinyatakan sebuah fungsi fn,a,b dengan fn,a,b(x)≡ax+b mod n untuk a,b,x bilangan bulat dan 0<a<n, 0≤b<n, 0≤x<n.
Kita akan menyebutr fn,a,b sebagai sebuah retraksi apabila fn,a,b(fn,a,b(x))≡fn,a,b(x) mod n untuk setiap 0≤x<n.
Misal R(n) adalah banyaknya retraksi untuk n.
F(N)=∑R(n4+4) untuk 1≤n≤N.
F(1024)=77532377300600.
Carilah F(107) (mod 1 000 000 007)
Answer: 0a9aa05f7bce906adb602af96ba06dc0
Soal 447
Untuk setiap bilangan bulat n>1, dinyatakan sebuah fungsi fn,a,b dengan fn,a,b(x)≡ax+b mod n untuk a,b,x bilangan bulat dan 0<a<n, 0≤b<n, 0≤x<n.
Kita akan menyebutr fn,a,b sebagai sebuah retraksi apabila fn,a,b(fn,a,b(x))≡fn,a,b(x) mod n untuk setiap 0≤x<n.
Misal R(n) adalah banyaknya retraksi untuk n.
F(N)=∑R(n) untuk 2≤n≤N.
F(107)≡638042271 (mod 1 000 000 007).
Carilah F(1014) (mod 1 000 000 007).
Answer: ea764a33b7368fccb4a1bbd37768d08c
Soal 448
Fungsi kpk(a,b) menyatakan kelipatan persekutuan terkecil dari a dan b.
Misal A(n) adalah rata-rata nilai dari kpk(n,i) untuk 1≤i≤n.
Sebagai contoh: A(2)=(2+2)/2=2 dan A(10)=(10+10+30+20+10+30+70+40+90+10)/10=32.
Misal S(n)=∑A(k) untuk 1≤k≤n.
S(100)=122726. Carilah S(99999999019) mod 999999017.
Answer: e6e7e87005c7b070cbc08ce727ae4e6a
Soal 449
Phil sang penjual manisan memproduksi persediaan baru dari permen berlapis cokelat. Setiap pusat permen berbentuk seperti sebuah ellipsoid yang permukaannya dinyatakan dengan persamaan: b2x2 + b2y2 + a2z2 = a2b2.
Phil ingin mengetahui berapa banyak cokelat yang dibutuhkan untuk menutupi satu buah permen dengan tersebar secara merata setebal satu milimeter.
| Jika a=1 mm dan b=1 mm, banyaknya cokelat yang diperlukan adalah |
|
π mm3 |
Carilah banyaknya cokelat yang diperlukan dalam mm3 jika a=3 mm dan b=1 mm. Berikan jawaban Anda yang telah dibulatkan hingga 8 angka di belakang koma.
Answer: 8ac19d0d06980691526883bc8c0950ef
Soal 450
Hiposikloid adalah kurva yang digambarkan oleh sebuah titik pada lingkaran kecil yang berputar di dalam lingkaran besar. Persamaan parametrik dari sebuah hiposikloid yagn berpusat pada titik origin O(0,0), dan dimulai dari titik yang paling kanan adalah:
$x(t) = (R - r) \cos(t) + r \cos(\frac {R - r} r t)$
$y(t) = (R - r) \sin(t) - r \sin(\frac {R - r} r t)$
Dimana R adalah panjang jari-jari dari lingkaran besar dan r adalah panjang jari-jari dari lingkaran kecil.
Misal $C(R, r)$ adalah himpunan titik-titik berbeda dengan koordinat bilangan bulat pada hiposiklid dengan panjang jari-jari R dan r, dan untuk nilai t yang bersesuaian sehingga $\sin(t)$ dan $\cos(t)$ adalah bilangan rasional.
Misal $S(R, r) = \sum_{(x,y) \in C(R, r)} |x| + |y|$ adalah hasil penjumlahan nilai mutlak dari koordinat x dan y dari titik-titik pada $C(R, r)$.
Misal $T(N) = \\sum_{R = 3}^N \\sum_{r=1}^{\\lfloor \\frac {R - 1} 2 \\rfloor} S(R, r)$ adalah hasil penjumlahan dari $S(R, r)$ untuk R dan r adalah bilangan bulat positif, $R\\leq N$ dan $2r < R$.
Diketahui:
C(3, 1) = {(3, 0), (-1, 2), (-1,0), (-1,-2)}
C(2500, 1000) =
-
{(2500, 0), (772, 2376), (772, -2376), (516, 1792),
(516, -1792), (500, 0), (68, 504), (68, -504),
(-1356, 1088), (-1356, -1088), (-1500, 1000), (-1500, -1000)}
S(3, 1) = (|3| + |0|) + (|-1| + |2|) + (|-1| + |0|) + (|-1| + |-2|) = 10
T(3) = 10; T(10) = 524 ;T(100) = 580442; T(103) = 583108600.
Carilah T(106).
Answer: d4ac68b5850e626fa95199b2b03efd53
Soal 451
Perhatikan bilangan 15.
Terdapat delapan buah bilangan positif kurang dari 15 yang koprima dengan 15: 1, 2, 4, 7, 8, 11, 13, 14.
Invers modular dari bilangan-bilangan tersebut yang telah di modulo 15 adalah: 1, 8, 4, 13, 2, 11, 7, 14
Karena
1*1 mod 15=1
2*8=16 mod 15=1
4*4=16 mod 15=1
7*13=91 mod 15=1
11*11=121 mod 15=1
14*14=196 mod 15=1
Misal I(n) adalah bilangan bulat positif m terbesar kurang dari n-1 sehingga invers modular dari m modulo n sama dengan m itu sendiri.
Sehingga I(15)=11.
Juga I(100)=51 dan I(7)=1.
Carilah ∑I(n) untuk 3≤n≤2·107
Answer: 9848878734a1d751a0e428147ab0b4aa
Soal 452
Dinyatakan F(m,n) sebagai banyaknya kumpulan n-buah bilangan bulat positif yang hasil kali dari elemen-elemennya tidak melebihi m.
F(10, 10) = 571.
F(106, 106) mod 1 234 567 891 = 252903833.
Carilah F(109, 109) mod 1 234 567 891.
Answer: a75f50818cab61a160cafa2c4145ed23
Soal 453
Sebuah bangun bersisi empat sederhana adalah sebuah poligon yang memiliki empat titik sudut berbeda, dan tidak ada sudut lurus dan tidak ada garis yang berpotongan.
Misal Q(m, n) adalah banyaknya bangun bersisi empat sederhana dimana titik-titik sudutnya memiliki koordinat bilangan bulat (x,y) yang memenuhi 0 ≤ x ≤ m dan 0 ≤ y ≤ n.
Sebagai contoh, Q(2, 2) = 94 dapat terlihat pada gambar berikut:

Dapat juga dibuktikan bahwa Q(3, 7) = 39590, Q(12, 3) = 309000 dan Q(123, 45) = 70542215894646.
Carilah Q(12345, 6789) mod 135707531.
Answer: 7f5ed466531a399174a64c6de41ea707
Soal 454
Dalam persamaan berikut x, y, dan n adalah bilangan bulat positif.
1 x |
+ | 1 y |
= | 1 n |
Untuk sebuah limit L kita nyatakan F(L) sebagai banyaknya solusi yang memenuhi x < y ≤ L.
Dapat dibuktikan bahwa F(15) = 4 dan F(1000) = 1069.
Carilah F(1012).
Answer: cf4e45f50c511e558b3dccb3ed481cb5
Soal 455
Misal f(n) adalah bilangan bulat positif x terbesar kurang dari 109 sehingga 0 digit terakhir dari nx membentuk bilangan x (termasuk angka nol di depan), atau fungsi akan menghasilkan nilai nol jika tidak ada bilangan bulat yang mampu memenuhi sifat di atas.
Sebagai contoh:
- f(4) = 411728896 (4411728896 = ...490411728896)
- f(10) = 0
- f(157) = 743757 (157743757 = ...567000743757)
- Σf(n), 2 ≤ n ≤ 103 = 442530011399
Carilah Σf(n), 2 ≤ n ≤ 106.
Answer: 22d6cf30a29e14e5c78dca980edc2796
Soal 456
Dinyatakan:
xn = (1248n mod 32323) - 16161
yn = (8421n mod 30103) - 15051
Pn = {(x1, y1), (x2, y2), ..., (xn, yn)}
Sebagai contoh, P8 = {(-14913, -6630), (-10161, 5625), (5226, 11896), (8340, -10778), (15852, -5203), (-15165, 11295), (-1427, -14495), (12407, 1060)}.
Misal C(n) adalah banyaknya segitiga yang titik sudutnya merupakan anggota Pn, dimana pada segitiga tersebut terdapat pusat koordinat O(0,0) pada bagian dalamnya.
Contoh:
C(8) = 20
C(600) = 8950634
C(40 000) = 2666610948988
Carilah C(2 000 000).
Answer: e2811a92b4658ca420be740f6c66572b
Soal 457
Misal f(n) = n2 - 3n - 1.
Misal p adalah bilangan prima.
Misal R(p) adalah bilangan bulat positif n terkecil sehingga f(n) mod p2 = 0 jika terdapat bilangan bulat n, jika tidak ada bilangan bulat n yang memenuhi sifat di atas, maka R(p) = 0.
Misal SR(L) adalah ∑R(p) untuk semua bilangan prima yang tidak melebihi L.
Carilah SR(107).
Answer: 5eae79c2f4887f6cf08c099840317a51
Soal 458
Terdapat himpunan huruf-huruf alfabet A yang berisi huruf-huruf pembentuk kata "project": A={c,e,j,o,p,r,t}.
Misal T(n) adalah banyaknya teks dengan panjang n yang terdiri dari huruf-huruf anggota himpunan A yang tidak memiliki sebuah substring dari 5040 permutasi pada huruf-huruf pembentuk kata "project".
T(7)=77-7!=818503. </P>
Carilah T(1012). Berikan 9 digit terakhir dari jawaban Anda.
Answer: d304abee61f0f6ac83a73de56d2fe578
Soal 459
Permainan membalik adalah permainan yang dimainkan oleh dua orang pada papan berisi kotak-kotak berukuran N x N.
Pada setiap kotak terdapat sebuah disk yang memiliki satu sisi putih dan satu sisi hitam.
Permainan dimulai dengan semua disk menunjukkan sisi bewarna putihnya.
Sebuah putaran yang dilakukan dengan membalikkan semua disk dalam sebuah persegi panjang besar dengan aturan sebagai berikut:
- pojok kanan atas dari persegi panjang haruslah berisi disk putih
- Lebar dari persegi panjang haruslah merupakan bilangan kuadrat sempurna (1, 4, 9, 16, ...)
- Panjang dari persegi panjang haruslah merupakan sebuah bilangan segitiga (1, 3, 6, 10, ...)

Kedua pemain melakukan hal ini secara bergantian. Pemain dikatakan menang apabila ia dapat membalik semua disk menjadi hitam.
Misal W(N) adalah banyaknya gerakan kemenangan untuk pemain pertama pada papan berisi kotak-kotak berukuran N x N yang semua disknya bewarna putih, dengan diasumsikan permainan berlangsung secara sempurna.
W(1) = 1, W(2) = 0, W(5) = 8 dan W(102) = 31395.
Untuk N=5, delapan buah gerakan kemenangan yang dapat dilakukan oleh pemain pertama pada giliran pertamanya adalah:


Carilah W(106).
Answer: abe2c990b8f028376186c2bc339e4c1e
Soal 460
Pada bidang Euclidean, seekor semut bergerak dari titik A(0, 1) ke titik B(d, 1) untuk bilangan bulat d.
Pada setiap langkahnya, semut pada titik (x0, y0) memilih salah satu koordinat bilangan bulat (x1, y1) yang memenuhi x1 ≥ 0 dan y1 ≥ 1 dan bergerak lurus ke (x1, y1) dengan kecepatan konstan v. Nilai dari v bergantung pada y0 dan y1 dengan aturan sebagai berikut:
- Jika y0 = y1, nilai dari v sama dengan y0.
- Jika y0 ≠ y1, nilai dari v sama dengan (y1 - y0) / (ln(y1) - ln(y0)).
Gambar di kiri adalah salah satu kemungkinan jalur untuk d = 4. Pertama-tama sang semut bergerak dari A(0, 1) ke P1(1, 3) dengan kecepatan (3 - 1) / (ln(3) - ln(1)) ≈ 1.8205. Maka waktu yang diperlukan adalah sqrt(5) / 1.8205 ≈ 1.2283.
Dari P1(1, 3) ke P2(3, 3) semut bergerak dengan kecepatan 3, sehingga waktu yang diperlukan adalah 2 / 3 ≈ 0.6667. Dari P2(3, 3) ke B(4, 1) semut bergerak dengan kecepatan (1 - 3) / (ln(1) - ln(3)) ≈ 1.8205 sehingga waktu yang diperlukan adalah sqrt(5) / 1.8205 ≈ 1.2283.
Sehingga total waktu yang diperlukan adalah 1.2283 + 0.6667 + 1.2283 = 3.1233.
Gambar di kanan adalah kemungkinan jalur lain. Total waktu yang diperlukan untuk jalur ini adalah 0.98026 + 1 + 0.98026 = 2.96052. Sehingga dapat terlihat bahwa jalur ini merupakan jalur tercepat untuk d = 4.

Misal F(d) adalah total waktu yang diperlukan jika semut memilih jalur tercepat. Sebagai contoh, F(4) ≈ 2.960516287.
Dapat dibuktikan bahwa F(10) ≈ 4.668187834 dan F(100) ≈ 9.217221972.
Carilah F(10000). Berikan jawaban Anda yang dibulatkan hingga sembilan angka di belakang koma.
Answer: 134fd9e25365ddb970971dd21f386408
Soal 461
Misal fn</var>(k) = ek/n - 1, untuk semua bilangan bulat tidak negatif k.
Luar biasanya, f200(6) + f200(75) + f200(89) + f200(226) = 3.141592644529… ≈ π.
Kenyataannya, cara ini merupakan cara terbaik untuk memperkirakan nilai π dalam bentuk fn(a) + fn(b) + fn(c) + fn(d) untuk n = 200.
Misal g(n) = a2 + b2 + c2 + d 2 untuk a, b, c, d yang akan meminimalisir error: | fn(a) + fn(b) + fn(c) + fn(d) - π|
(dimana |x| menyatakan nilai mutlak dari x).
Anda diberikan informasi bahwa g(200) = 62 + 752 + 892 + 2262 = 64658.
Carilah g(10000).
Answer: 70c3eff774c9d5cdb29284c16b9d1bc6
Soal 462
Bilangan halus-3 adalah sebuah bilangan bulat yang tidak memiliki faktor prima lebih dari 3. Untuk sebuah bilangan bulat N, kita nyatakan S(N) sebagai himpunan dari bilangan halus-3 kurang dari atau sama dengan N. Sebagai contoh, S(20) = { 1, 2, 3, 4, 6, 8, 9, 12, 16, 18 }.
Kita nyatakan F(N) sebagai banyaknya permutasi dari S(N) dimana setiap elemen muncul setelah semua faktornya terlebih dahulu muncul.
Berikut ini adalah salah satu contoh permutasi yang mungkin dari N = 20.
- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12.
Tetapi ini bukanlah merupakan permutasi yang valid, karena 12 muncul sebelum faktornya, yaitu 6 muncul.
- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18.
Kita dapat membuktikan bahwa F(6) = 5, F(8) = 9, F(20) = 450 dan F(1000) ≈ 8.8521816557e21.
Carilah F(1018). Berikan jawaban Anda dalam notasi ilmiahnya dibulatkan hingga sepuluh angka di belakang koma.
Saat memberikan jawaban Anda, gunakan huruf e kecil untuk memisahkan mantissa dan eksponen. Sebagai contoh, jika misalkan jawaban Anda adalah 112,233,445,566,778,899 maka format jawaban yang harus diberikan adalah 1.1223344557e17.
Answer: 77c84f6238d9987d204eb771d3dcde13
Soal 463
Fungsi $f$ yang dinyatakan untuk semua bilangan bulat positif adalah sebagai berikut:
- $f(1)=1$
- $f(3)=3$
- $f(2n)=f(n)$
- $f(4n + 1)=2f(2n + 1) - f(n)$
- $f(4n + 3)=3f(2n + 1) - 2f(n)$
Fungsi $S(n)$ dinyatakan sebagai $\sum_{i=1}^{n}f(i)$.
$S(8)=22$ dan $S(100)=3604$.
Carilah $S(3^{37})$. Berikan 9 digit terakhir dari jawaban Anda.
Answer: 95481696a65b0c1d9f73186a693686f5
Soal 464
Fungsi Möbius, yang dilambangkan dengan μ(n), dinyatakan sebagai:
- μ(n) = (-1)ω(n) jika n adalah bilangan squarefree (dimana ω(n) adalah banyaknya faktor prima berbeda dari n)
- μ(n) = 0 jika n bukanlah merupakan bilangan squarefree.
Misal P(a,b) adalah banyaknya bilangan bulat n yang berada pada interval [a,b] sehingga μ(n) = 1.
Misal N(a,b) adalah banyaknya bilangan bulat n yang berada pada interval [a,b] sehingga μ(n) = -1.
Sebagai contoh, P(2,10) = 2 dan N(2,10) = 4.
Misal C(n) adalah banyaknya pasangan bilangan bulat (a,b) sehingga:
- 1 ≤ a ≤ b ≤ n,
- 99·N(a,b) ≤ 100·P(a,b), dan
- 99·P(a,b) ≤ 100·N(a,b).
Sebagai contoh, C(10) = 13, C(500) = 16676 dan C(10 000) = 20155319.
Carilah C(20 000 000).
Answer: 6d3598e116ae19efe33063bccf0b693b
Soal 465
Kernel dari sebuah poligon dinyatakan sebagai himpunan wilayah yang dapat terlihat dari semua titik pada keliling poligon. Kita nyatakan poligon polar sebagai sebuah poligon dimana titik origin O(0,0) harus berada di dalam kernelnya.
Untuk permasalahan ini, sebuah poligon dapat memiliki beberapa titik yang berada di dalam satu garis lurus. Tetapi, sebuah poligon tetap tidak diperbolehkan untuk memiliki sisi yang saling berpotongan, dan tidak bisa memiliki luas wilayah sebesar nol.
Sebagai contoh, hanya gambar pertama yang merupakan poligon polar (kernel pada gambar kedua, ketiga, dan keempat tidak memuat titik origin di dalamhya, dan pada gambar kelima tidak terdapat kernel sama sekali):

Perhatikan bahwa poligon pertama mempunyai tiga buah titik yang berada pada satu garis lurus.
Misal P(n) adalah banyaknya poligon polar sehingga titik (x, y) merupakan koordinat bilangan bulat yang nilai mutlaknya tidak lebih dari n.
Perlu diingat bahwa poligon harus dianggap berbeda jika mereka memiliki himpunan titik-titik yang berbeda, walaupun mereka memiliki bentuk dan luas yang sama. Sebagai contoh, poligon dengan titik-titik sudut [(0,0),(0,3),(1,1),(3,0)] adalah berbeda dengan poligon dengan titik-titik sudut [(0,0),(0,3),(1,1),(3,0),(1,0)].
Sebagai contoh, P(1) = 131, P(2) = 1648531, P(3) = 1099461296175 dan P(343) mod 1 000 000 007 = 937293740.
Carilah P(713) mod 1 000 000 007.
Answer: 64de4b2572602c3bdea4b4360a694ca7
Soal 466
Misal P(m,n) adalah banyaknya suku berbeda pada tabel perkalian berukuran m×n.
Sebagai contoh, sebuah tabel perkalian berukuran 3×4 akan terlihat seperti ini:
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
Terdapat 8 buah suku berbeda {1,2,3,4,6,8,9,12}, sehingga P(3,4) = 8.
Anda diberikan informasi:
P(64,64) = 1263,
P(12,345) = 1998, dan
P(32,1015) = 13826382602124302.
Carilah P(64,1016).
Answer: ff8b91e50170810dccd15ea59fb5efd8
Soal 467
Sebuah bilangan bulat s akan disebut sebagai sebuah bilangan bulat super dari bilangan bulat n , jika digit-digit dari n membentuk sebuah sub-barisan dari digit-digit s.
Sebagai contoh, 2718281828 adalah bilangan bulat super dari 18828, sementara 314159 bukan merupakan bilangan bulat super dari 151.
Misal p(n) adalah bilangan prima ke-n, dan misal c(n) adalah bilangan komposit ke-n. Sebagai contoh, p(1) = 2, p(10) = 29, c(1) = 4 dan c(10) = 18.
{p(i) : i ≥ 1} = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...}
{c(i) : i ≥ 1} = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, ...}
Misal PD adalah barisan dari hasil penjumlahan digit-digit dari {p(i)} (CD dinyatakan dengan cara yang sama untuk {c(i)}):
PD = {2, 3, 5, 7, 2, 4, 8, 1, 5, 2, ...}
CD = {4, 6, 8, 9, 1, 3, 5, 6, 7, 9, ...}
Misal Pn adalah bilangan bulat yang dibentuk dengan menggabungkan n buah elemen pertama dari PD (Cn dinyatakan dengan cara yang sama untuk CD).
P10 = 2357248152
C10 = 4689135679
Misal f(n) adalah bilangan bulat positif terkecil yang memiliki bilangan bulat super yang sama antara Pn dan Cn.
Sebagai contoh, f(10) = 2357246891352679, dan f(100) mod 1 000 000 007 = 771661825.
Carilah f(10 000) mod 1 000 000 007.
Answer: 3ee327e7b4415f9e1cb75e3363c388b5
Soal 468
Sebuah bilangan bulat B disebut halus apabila tidak ada faktor primanya yang tidak lebih dari B.
Misal SB(n) adalah faktor halus B terbesar dari n.
Contoh:
S1(10) = 1
S4(2100) = 12
S17(2496144) = 5712
Dinyatakan F(n) = ∑1≤B≤n ∑0≤r≤n SB(C(n,r)). Pada soal ini, C(n,r) melambangkan koefisien binomial.
Contoh:
F(11) = 3132
F(1 111) mod 1 000 000 993 = 706036312
F(111 111) mod 1 000 000 993 = 22156169
Carilah F(11 111 111) mod 1 000 000 993.
Answer: b7aa617d57bf1947ddfb9ae47c0feaac
Soal 469
Pada suatu ruangan N bangku diletakkan di sekliling meja bundar.
Satu per satu ksatria memasuki ruangan dan menempati bangku kosong secara acak.
Agar dapat memiliki ruang siku tangan yang cukup, para ksatria selalu akan membiarkan setidaknya satu kursi kosong antar tiap orang.
Saat tidak ada lagi bangku yang tersisa, dinyatakan C bagian dari kursi kosong.
Kita juga akan menyatakan E(N) sebagai nilai harapan (expected value) dari C.
Dapat dibuktikan bahwa E(4) = 1/2 dan E(6) = 5/9.
Carilah E(1018). Berikan jawaban Anda dibulatkan hingga empat belas angka di belakang koma dengan format 0.abcdefghijklmn.
Answer: 3c2b641262880db5b735cfa4d4c957bc
Soal 470
Pada sebuah permainan Ramvok:
Misal t menyatakan banyaknya giliran maksimal yang akan berlangsung. Jika t = 0, maka permainan akan langsung selesai saat itu juga. Jika t ≠ 0, pada setiap giliran ke-i, pemain akan memutar sebuah dadu. Setelah memutarnya, jika i < t maka pemain dapat memberhentikan permainan dan menerima hadiah sesuai dengan nilai dadu yang dia dapatkan pada putaran ini, atau mengabaikan nilai pada dadu dan mencoba melempar dadu lagi di giliran selanjutnya. Jika i = t, maka nilai dadu yang muncul tidak dapat diabaikan, dan hadiah yang didapatkan harus diterima. Sebelum permainan dimulai, angka t dipilih oleh pemain, yang kemudian akan menjadi biaya harus dibayarkan pada awal permainan sebesar ct untuk suatu konstanta c. Untuk c = 0, dapat dipilih nilai t tak terhingga (dengan biaya di awal permainan sebesar 0). Misal R(d, c) adalah nilai keuntungan harapan (expected profit) (yang dihitung adalah pendapatan bersih) yang seorang pemain dapatkan dari sebuah permainan Ramvok yang dimainkan dengan baik, diberikan dadu dengan d-buah sisi, dan konstanta biaya c. Sebagai contoh, R(4, 0.2) = 2.65. Asumsikan bahwa sang pemain memiliki uang yang cukup untuk memainkan semua permainan dengan biaya berapapun.
Sekarang perhatikan sebuah permainan Ramvok Super:
Pada Ramvok Super, permainan Ramvok dimainkan berulang-ulang, namun dengan sedikit modifikasi. Setelah satu permainan, dadu yang digunakan akan diubah. Proses pengubahan dadunya adalah sebagai berikut: Dadu diputar satu kali, dan jika dadu tersebut mengeluarkan sisi yang memiliki nilai, maka sisi tersebut akan diubah menjadi kosong. Dan jika sisi tersebut sudah kosong, maka sisi tersebut akan diubah kembali menjadi nilai awalnya. Setelah perubahan dadu dilakukan, permainan Ramvok dapat dimulai kembali (dan pada setiap permainan, pada setiap giliran, dadu akan diputar sampai sisi yang ada nilainya muncul). Pemain selalu dapat mengetahui sisi mana dari dadu yang kosong dan sisi mana dari dadu yang memiliki nilai. Permainan Ramvok Super akan berakhir saat semua dadu menjadi kosong.
Misal S(d, c) adalah besar keuntungan harapan (expected profit) yang akan didapati oleh pemain dari permainan Ramvok Super yang dimainkan secara baik, jika digunakan dadu dengan d-buah sisi (yang semua sisinya dapat terlihat), dan konstanta biaya c. Sebagai contoh, S(6, 1) = 208.3.
Misal F(n) = ∑4≤d≤n ∑0≤c≤n S(d, c).
Hitunglah F(20), dibulatkan ke bilangan bulat terdekat.
Answer: a37644507221e441ca9667e1c7e660c4
Soal 471
Segitiga ΔABC berada di dalam elips dengan persamaan $\frac {x^2} {a^2} + \frac {y^2} {b^2} = 1$, 0 < 2b < a, a dan b adalah bilangan bulat.
Misal r(a,b) adalah panjang jari-jari dari lingkaran dalam segitiga ΔABC saat lingkaran dalam berpusat di (2b, 0) dan memiliki salah satu koordinat koordinat $\left( \frac a 2, \frac {\sqrt 3} 2 b\right)$.
Sebagai contoh, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.


Misal $G(n) = \sum_{a=3}^n \sum_{b=1}^{\lfloor \frac {a - 1} 2 \rfloor} r(a, b)$
Diberikan informasi G(10) = 20.59722222, G(100) = 19223.60980 (dibulatkan hingga 10 angka di belakang koma).
Carilah G(1011).
Berikan jawaban Anda dalam notasi ilmiah yang dibulatkan hingga 10 angka di belakang koma. Gunakan huruf e kecil untuk memisahkan mantissa dan eksponen.
Untuk G(10) jawabannya adalah 2.059722222e1.
Answer: d632b70a0a349ed70ac17ef6246dd7d8
Soal 472
Terdapat N buah bangku pada suatu baris. N orang datang satu per satu untuk menempati bangku dengan aturan berikut:
- Tidak ada orang yang duduk bersebelahan.
- Orang pertama dapat duduk di bangku manapun.
- Orang berikutnya memilih bangku yang memiliki jarak paling jauh dari orang lain yang telah duduk, sepanjang tidak melanggar aturan ke 1. Jika terdapat lebih dari satu bangku yang memenuhi sifat ini, maka orang tersebut akan memilih bangku yang paling kiri dari pilihan bangku-bangku yang memenuhi sifat ini.
Perlu diingat bahwa karena adanya aturan ke 1, beberapa bangku dipastikan akan kosong, dan banyak maksimum orang yang akan duduk adalah kurang dari N (untuk N > 1).
Ini adalah contoh penempatan yang mungkin untuk N = 15:

Dapat kita lihat bahwa apabila orang pertama memilih bangku yang benar, maka 15 bangku tersebut dapat memuat hingga 7 orang.
Kita juga dapat melihat bahwa orang pertama memiliki 9 pilihan agar terdapat sebanyak mungkin jumlah orang yang dapat duduk.
Misal f(N) adalah banyaknya pilihan bangku yang dapat dipilih oleh orang pertama agar terdapat sebanyak mungkin jumlah orang yang dapat duduk pada barisan bangku berisi N-buah kursi. Sehingga, f(1) = 1, f(15) = 9, f(20) = 6, dan f(500) = 16.
Juga, ∑f(N) = 83 untuk 1 ≤ N ≤ 20 dan ∑f(N) = 13343 untuk 1 ≤ N ≤ 500.
Carilah ∑f(N) untuk 1 ≤ N ≤ 1012. Berikan 8 digit terakhir dari jawaban Anda.
Answer: 7d7ff31d9448e86ba9c901878c1fa5c6
Soal 473
Misal $\varphi$ adalah rasio emas: $\varphi=\frac{1+\sqrt{5}}{2}.$
Luar biasanya, kita dapat menulis semua bilangan bulat positif sebagai hasil penjumlahan dari pemangkatan $\varphi$, dan setiap pangkat dari $\varphi$ hanya perlu digunakan satu kali pada penjumlahan ini.
Tetapi representasi ini tidaklah unik.
Kita dapat membuatnya menjadi unik dengan cara membuat tidak ada bilangan pangkat yang berurutan yang digunakan dan hasil representasinya haruslah tertentu.
Sebagai contoh: $2=\varphi+\varphi^{-2}$ dan $3=\varphi^{2}+\varphi^{-2}$
Untuk merepresentasikan hasil penjumlahan dari pemangkatan $\varphi$, kita akan gunakan angka 0 dan 1 dengan tujuan untuk menandakan dimana eksponen yang negatif berada.
Kita akan menyebut representasi bilangan ini sebagai basis bilangan phigital.
Sehingga $1=1{\varphi}$, $2=10.01{\varphi}$, $3=100.01{\varphi}$ dan $14=100100.001001{\varphi}$.
bilangan basis phigital yang merepresentasikan bilangan 1, 2 dan 14 merupakan bilangan palindrom, sementara bilangan basis phigital dari bilangan 3 bukan merupakan bilangan palindrom.
(tanda titik pada basis phigital bukanlah merupakan titik tengah dari palindrom).
Hasil penjumlahan dari bilangan bulat positif yang tidak melebihi 1000, dimana representasi phigitalnya merupakan bilangan palindrom adalah 4345.
Carilah hasil penjumlahan bilangan bulat positif yang tidak melebihi $10^{10}$ dimana representasi phigitalnya merupakan bilangan palindrom.
Answer: a4ea7a2040b6385b6d12863fd693e434
Soal 474
Untuk sebuah bilangan bulat positif n dan digit d, kita nyatakan F(n, d) sebagai banyaknya faktor dari n yang digit terakhirnya sama dengan d.
Sebagai contoh, F(84, 4) = 3. Diantara faktor-faktor dari 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), tiga diantaranya (4, 14, 84) mempunyai digit terakhir 4.
Kita juga dapat membuktikan bahwa F(12!, 12) = 11 dan F(50!, 123) = 17888.
Carilah F(106!, 65432) modulo (1016 + 61).
Answer: dcfd11c680aa4cce11e1eee1a448440c
Soal 475
12n musisi ikut serta pada sebuah festival musik. Pada hari pertama, mereka membentuk 3n kuartet dan berlatih setiap hari.
Namun terjadi sebuah bencana. Pada akhir hari itu, semua musisi memutuskan bahwa mereka tidak mau lagi untuk bermain musik dengan setiap anggota dari kuartetnya.
Pada hari kedua, mereka membentuk 4n trio, setiap musisi menghindari mementuk trio dengan rekan pada kuartet di hari sebelumnya.
Misal f(12n) adalah banyaknya cara untuk mengatur trio dari 12n musisi.
Anda diberikan informasi f(12) = 576 dan f(24) mod 1 000 000 007 = 509089824.
Carilah f(600) mod 1 000 000 007.
Answer: 6be2411783d9ca8e7ad174b269a85be5
Soal 476
Misal R(a, b, c) adalah luas maksimum yang dapat ditutupi oleh tiga buah lingkaran yang tidak saling menumpuk satu sama lain, yang terletak di dalam sebuah segitiga dengan panjang sisi a, b dan c.
Misal S(n) adalah nilai rata-rata dari R(a, b, c) atas semua kumpulan bilangan bulat (a, b, c) sehingga 1 ≤ a ≤ b ≤ c < a + b ≤ n
Anda diberikan informasi S(2) = R(1, 1, 1) ≈ 0.31998, S(5) ≈ 1.25899.
Carilah S(1803) dibulatkan hingga 5 angka di belakang koma.
Answer: 4d6a99b2a0f22af561aeeb69c0126fef
Soal 477
Sebuah permainan barisan bilangan dimulai dengan sebuah barisan bilangan S yang memiliki N-buah bilangan yang tertulis pada suatu barisan.
Dua orang memainkan permainan secara bergantian. Pada gilirannya, seorang pemain harus memilih dan mengambil salah satu diantara bilangan yang pertama atau yang terakhir yang masih terdapat ada di barisan.
Nilai yang didapatkan oleh pemain adalah hasil penjumlahan dari semua bilangan yang telah diambil. Setiap pemain akan berusaha untuk mendapatkan hasil penjumlahan terbesar.
Jika N = 4 dan S = {1, 2, 10, 3}, maka setiap pemain akan berusaha mendapatkna nilai terbesar dengan cara berikut:
- Pemain 1: mengambil bilangan pertama (1)
- Pemain 2: mengambil bilangan terakhir yang masih tersisa di barisan (3)
- Pemain 1: mengambil bilangan terakhir yang masih tersisa di barisan (10)
- Pemain 2: mengambil bilangan yang masih tersisa di barisan (2)
Skor pemain 1 adalah 1 + 10 = 11.
Misal F(N) adalah besar skor pemain 1 apabila kedua pemain saling berusaha untuk mendapatkan nilai terbesar pada permainan barisan bilangan dengan barisan S = {s1, s2, ..., sN} yang dinyatakan dengan:
- s1 = 0
- si+1 = (si2 + 45) modulo 1 000 000 007
Barisan ini dimulai dengan S = {0, 45, 2070, 4284945, 753524550, 478107844, 894218625, ...}.
Anda diberikan informasi bahwa F(2) = 45, F(4) = 4284990, F(100) = 26365463243, F(104) = 2495838522951.
Carilah F(108).
Answer: 4eb1b9788c1c6bed02f98d25c5633a21
Soal 478
Terdapat sebuah campuran dari tiga buah zat: A, B dan C. Sebuah campuran dapat dideskripsikan dengan rasio dari banyaknya zat A, B, dan C yang ada padanya dalam bentuk penulisan (a : b : c). Sebagai contoh, sebuah campuran dideskripsikan dengan rasio (2 : 3 : 5) mengandung 20% A, 30% B dan 50% C.
Untuk permasalahan pada soal ini, kita tidak dapat memisahkan masing-masing zat dari campuran. Tetapi, kita dapat mencampurkan dua campuran yang memiliki rasio kandungan zat berbeda untuk membentuk campuran dengan rasio baru.
Sebagi contoh, misalkan kita mempunyai tiga buah campuran dengan rasio masing-masing (3 : 0 : 2), (3 : 6 : 11) dan (3 : 3 : 4). Dengan mencampurkan 10 unit campuran pertama, 20 unit campuran kedua dan 30 unit campuran ketiga, kita bisa mendapatkan campuran baru dengan rasio (6 : 5 : 9), karena:
(10·3/5 + 20·3/20 + 30·3/10 : 10·0/5 + 20·6/20 + 30·3/10 : 10·2/5 + 20·11/20 + 30·4/10)
= (18 : 15 : 27) = (6 : 5 : 9)
Tetapi, dengan tiga campuran yang sama seperti di atas, adalah mustahil untuk membentuk campuran baru dengan rasio (3 : 2 : 1), karena banyaknya zat B pasti selalu lebih kecil dari zat C.
Misal n adalah sebuah bilangan bulat positif. Seharusnya untuk setiap tripel bilangan bulat (a, b, c) dengan 0 ≤ a, b, c ≤ n dan fpb(a, b, c) = 1, kita akan mempunyai campuran dengan rasio (a : b : c). Misal M(n) adalah himpunan dari semua campuran yang memiliki sifat di atas.
Sebagai contoh, M(2) memiliki 19 macam campuran dengan rasio-rasio sebagai berikut:
{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1),
(1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1),
(1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1),
(2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
Misal E(n) adalah banyaknya himpunan bagian dari M(n) yang dapat menghasilkan campuran dengan rasio (1 : 1 : 1), atau dengan kata lain, campuran yang memiliki jumlah yang sama antara zat A, B dan C.
Dapat dibuktikan bahwa E(1) = 103, E(2) = 520447, E(10) mod 118 = 82608406 dan E(500) mod 118 = 13801403.
Carilah E(10 000 000) mod 118.
Answer: 02760aada255f7a5246b6ddc96b70a52
Soal 479
Misal ak, bk, dan ck adalah tiga solusi (baik berupa bilangan real maupun kompleks) pada persamaan 1/x = (k/x)2(k+x2) - kx.
Sebagai contoh, untuk k = 5, dapat kita lihat bahwa {a5, b5, c5} diperkirakan {5.727244, -0.363622+2.057397i, -0.363622-2.057397i}.
Misal S(n) = Σ (ak+bk)p(bk+ck)p(ck+ak)p untuk semua bilangan bulat p, k sehingga 1 ≤ p, k ≤ n.
Menariknya, S(n) akan selalu merupakan bilangan bulat. Sebagai contoh, S(4) = 51160.
Carilah S(106) modulo 1 000 000 007.
Answer: b64da7e8067be18d8145d3b550240d90
Soal 480
Perhatikan semua susunan kata yang dapat dibentuk dengan memilih huruf-huruf, dengan urutan apapun, dari frasa:
Jika dibuat susunan kata kurang dari atau sama dengan 15 huruf, yang sesuai dengan urutan abjad, dan susunan-susunan tersebut diberi nomor secara berurutan dimulai dari angka 1.
Maka daftarnya akan menjadi:
- 1 : a
- 2 : aa
- 3 : aaa
- 4 : aaaa
- 5 : aaaaa
- 6 : aaaaaa
- 7 : aaaaaac
- 8 : aaaaaacd
- 9 : aaaaaacde
- 10 : aaaaaacdee
- 11 : aaaaaacdeee
- 12 : aaaaaacdeeee
- 13 : aaaaaacdeeeee
- 14 : aaaaaacdeeeeee
- 15 : aaaaaacdeeeeeef
- 16 : aaaaaacdeeeeeeg
- 17 : aaaaaacdeeeeeeh
- ...
- 28 : aaaaaacdeeeeeey
- 29 : aaaaaacdeeeeef
- 30 : aaaaaacdeeeeefe
- ...
- 115246685191495242: euleoywuttttsss
- 115246685191495243: euler
- 115246685191495244: eulera
- ...
- 525069350231428029: ywuuttttssssrrr
Dinyatakan P(w) sebagai posisi dari kata w.
Dinyatakan W(p) sebagai kata yang berada di posisi p.
Dapat kita lihat bahwa P(w) dan W(p) adalah merupakan fungsi saling invers: P(W(p)) = p dan W(P(w)) = w.
Contoh:
- W(10) = aaaaaacdee
- P(aaaaaacdee) = 10
- W(115246685191495243) = euler
- P(euler) = 115246685191495243
Carilah W(P(legionary) + P(calorimeters) - P(annihilate) + P(orchestrated) - P(fluttering)).
Berikan jawaban Anda menggunakan huruf kecil (tanpa tanda baca ataupun tanda spasi).
Answer: b97e157bf53033d21f610d2350b92faf